2.机器学习基石 | 感知器

Perception 感知器（用于线性二分类）

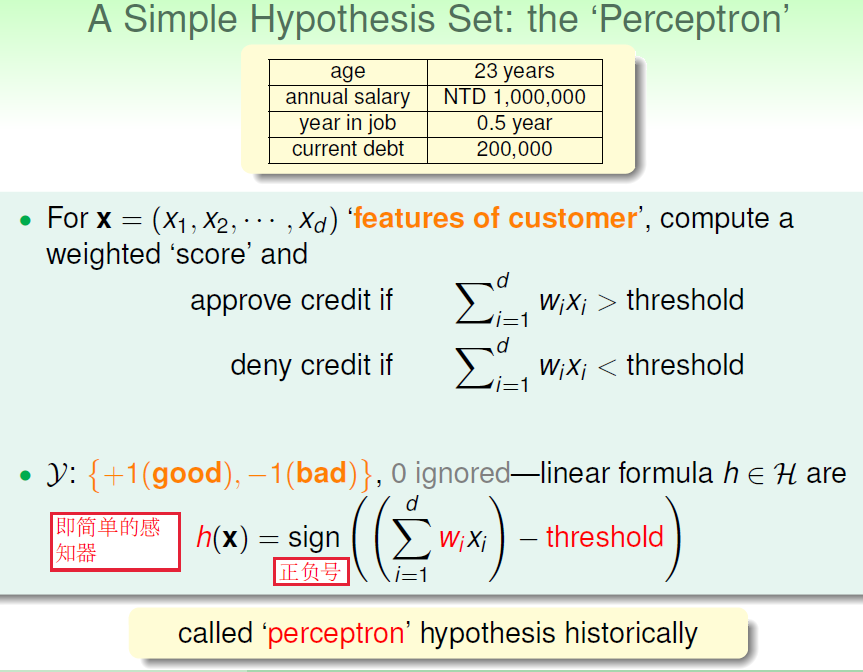
PLA算法 : 怎样从假设空间 $H$ 中找到 $g$

1.目标：g 约等于 f，最好的结果，但是f未知此方法不行


2.目标：使得在给定数据上两者预测结果接近

3.感知器优化算法（PLA）

上述公式的理解：
（1）y是正的，出来结果w是负的

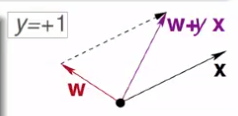
通过w+x，将w拉回来一点（作为新的分界面法向量，此图中黑色x为原分界面法向量）


（2）y是负的，出来结果w是正的

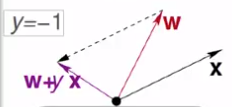
通过w+x，将w拉过去一点

举例：

（1）最开始没有线



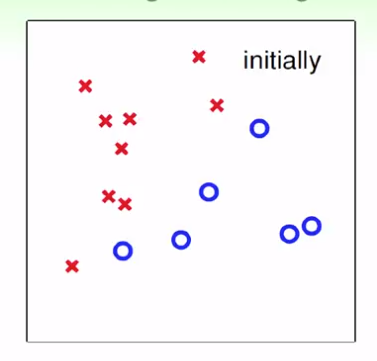
（2）默认每个点都是错的，找到任意一点与原点连线（原点在图中间），而这个点刚好为正（圈为正，叉为负），即为分界面的法向量




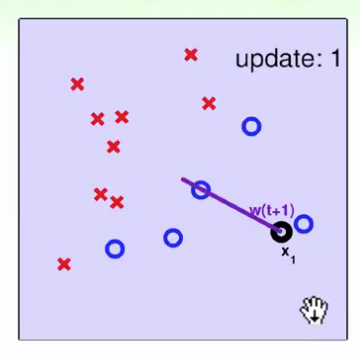
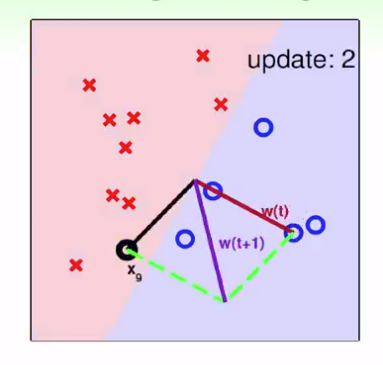
（3）
黑点为分类错误的点，与原法向量相加，产生紫色线，即可以调整分界面，紫色作为新的法向量，如此持续，直到没有分类错误



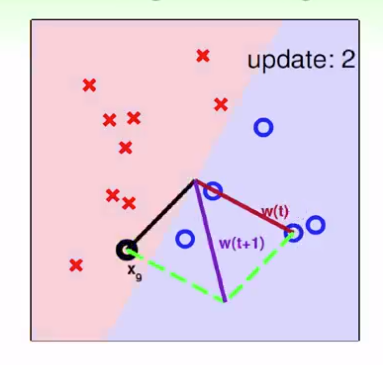
思考：

通过一次的调整，可以使得错误的点偏向正确一点点，但不是完全保证一定正确

PLA终止条件

1.PLA保证：数据必须线性可分



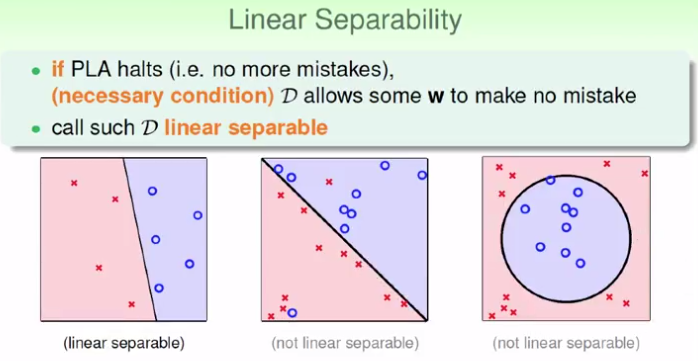
2.PLA条件1：线性可分



3.PLA条件2：有错才更新



结合条件1和2的结论：令

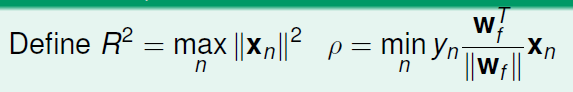
则由（1）得：
对于第T次更新，
$w_f^T\ast w_T>w_f^T\ast w_0+T\ast \rho \ast ||w_f||=T\ast \rho \ast ||w_f||$
(因为$w_0=0$)

由（2）得：

对于第T次更新，
$w_f^T\ast w_T>w_f^T\ast w_0+T\ast \rho \ast ||w_f||=T\ast \rho \ast ||w_f||$
从而(1)结果除以(2):
$\frac{w_f^T\ast w_T}{||w_T||})>\frac{T\ast \rho \ast ||w_f||}{\sqrt{T}\ast R}$

$\frac{w_f^T\ast w_T}{||w_T||\ast ||w_f||}>\sqrt{T}\frac{\rho }{R}$

而$\frac{w_f^T\ast w_T}{||w_T||\ast ||w_f||}$ 即两个向量的相似度，最大不超过1，故

$1>\sqrt{T}\frac{\rho }{R}$，最大更新次数 T 不超过 $\frac{R^2}{{\rho }^2}$

PLA优缺点分析

（1）优点：比较容易去实现
（2）缺点：
1.假定数据线性可分，但事实上我们不知道数据的分布
2.不确定多久才会终止，因为上述条件中的 $\rho$ 与 $w_f$ 有关，但 $w_f$ 未知

解决上述缺点

即使数据线性可分，当数据有噪声时PLA应该如何停止？

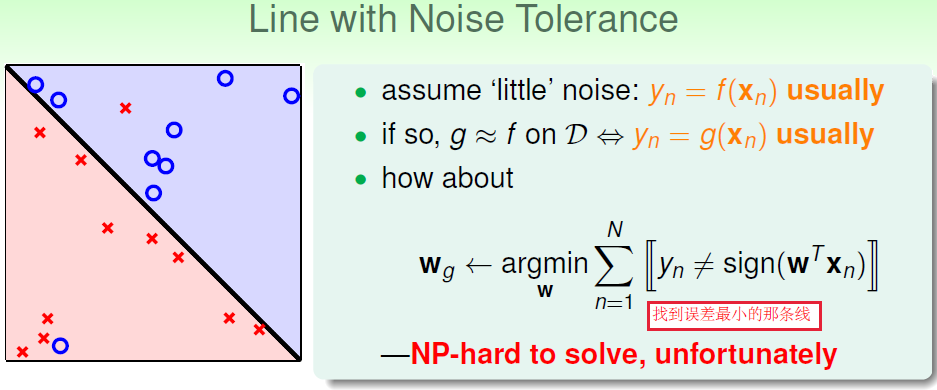
解决方法：
1.口袋算法（贪心算法，PLA的一个变形）

两者比较：

当线性可分时，口袋算法对于每条线，需要找出所有错误分类的点，而PLA只需要找到一个即可