归并排序-java实现

基本思想：
归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起，即分而治之)。

如图：

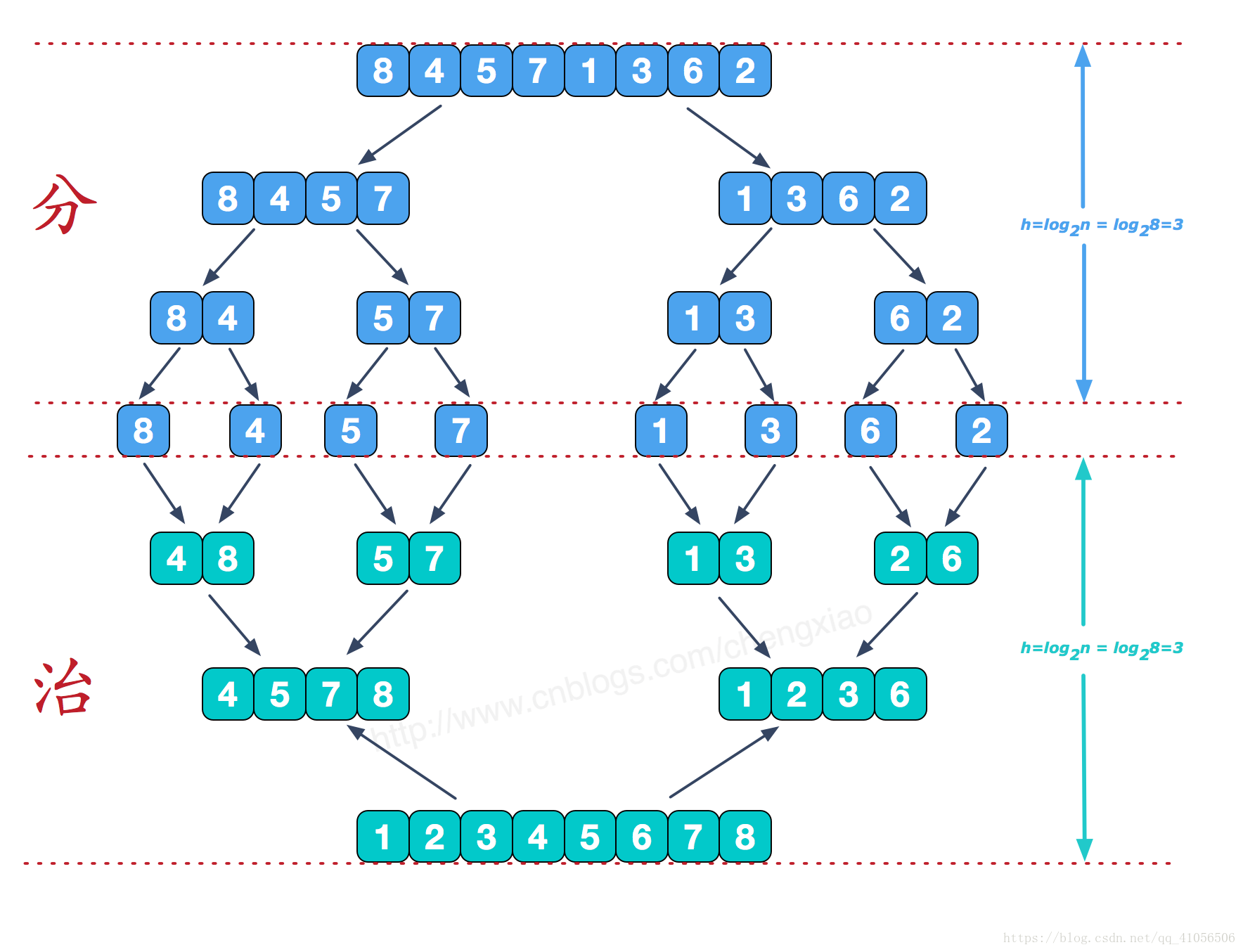
可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

合并相邻的子数列：
再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤

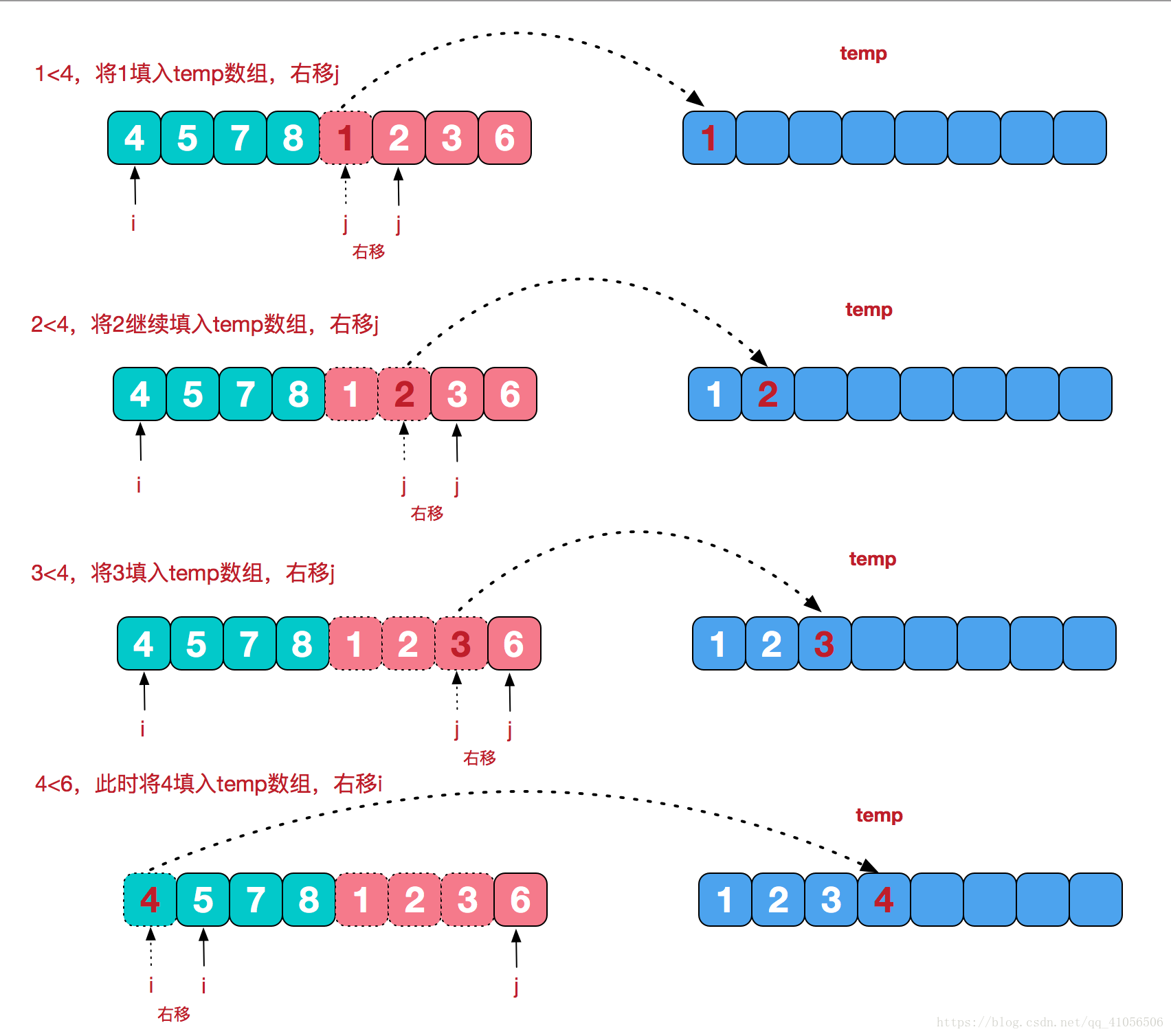
代码实现：

package Sort.Merge;

import Common.Common;
//自顶向下的归并排序
public class Merge {
    private static void sort(int[] a,int low,int high) {
        int mid=(low+high)/2;
        if (low<high) {
            sort(a, low, mid);//左边归并排序，使得左子序列有序
            sort(a, mid+1, high);//右边归并排序，使得右子序列有序
            merge(a, low, mid, high);//将两个有序子数组合并操作
        }
    }
    public static void merge(int[] a,int  low,int mid,int high) {
        int[] temp=new int[high-low+1];
        int i=low;//右列指针
        int j=mid+1;//左序列指针
        int k=0;//临时数组指针
        while (i<=mid&&j<=high) {
            //右边小于左边，将右边放入临时数组
            if (a[i]<a[j]) {
                temp[k++]=a[i++];
            }
            //左边小于右边将左边放入临时数组
            else {
                temp[k++]=a[j++];
            }
        }
//      System.out.println(k);
        //将右边未放完的元素继续放入临时数组
        while (i<=mid) {
            temp[k++]=a[i++];
        }
        //将左边未放完的元素继续放入临时数组
        while (j<=high) {
            temp[k++]=a[j++];
        }
        //将临时数组元素放入原数组中
        for (int x = 0; x < temp.length; x++) {
            a[x+low]=temp[x];
        }
    }
    public static void main(String[] args) {
        int[] in= {1,5,4,3,7,9,8,6};
        int low=0;
        int high=in.length-1;
        sort(in, low, high);
        for (int i = 0; i < in.length; i++) {
            System.out.print(in[i]+" ");
        }
    }

}

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。