剑指 Offer 34. 二叉树中和为某一值的路径

剑指 Offer 34. 二叉树中和为某一值的路径

难度：$middle$

---

题目描述

给你二叉树的根节点 $root$ 和一个整数目标和 $targetSum$ ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

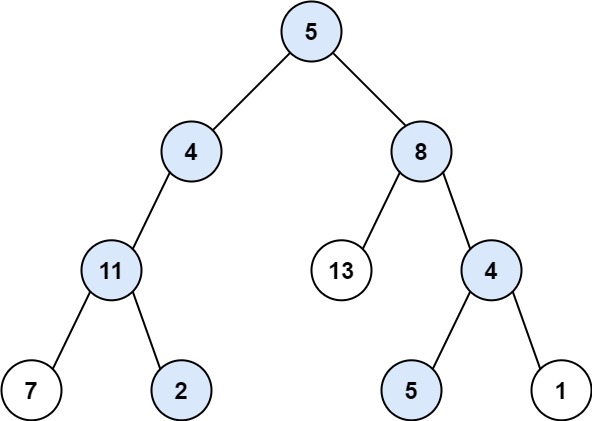
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]
复制示例输入

示例 2：

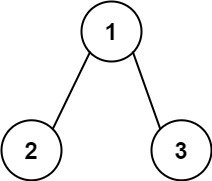
输入：root = [1,2,3], targetSum = 5
输出：[]
复制示例输入

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]
复制示例输入

提示：

• 树中节点总数在范围 $[0,5000]$ 内
• $-1000<=Node.val<=1000$
• $-1000<=targetSum<=1000$

注意：本题与主站 113 题相同：https://leetcode-cn.com/problems/path-sum-ii/

---

算法

(递归)

• 先序遍历： 按照 “根、左、右” 的顺序，遍历树的所有节点。
• 路径记录： 在先序遍历中，记录从根节点到当前节点的路径。当路径为 ① 根节点到叶节点形成的路径 且 ② 各节点值的和等于目标值 sum 时，将此路径加入结果列表。

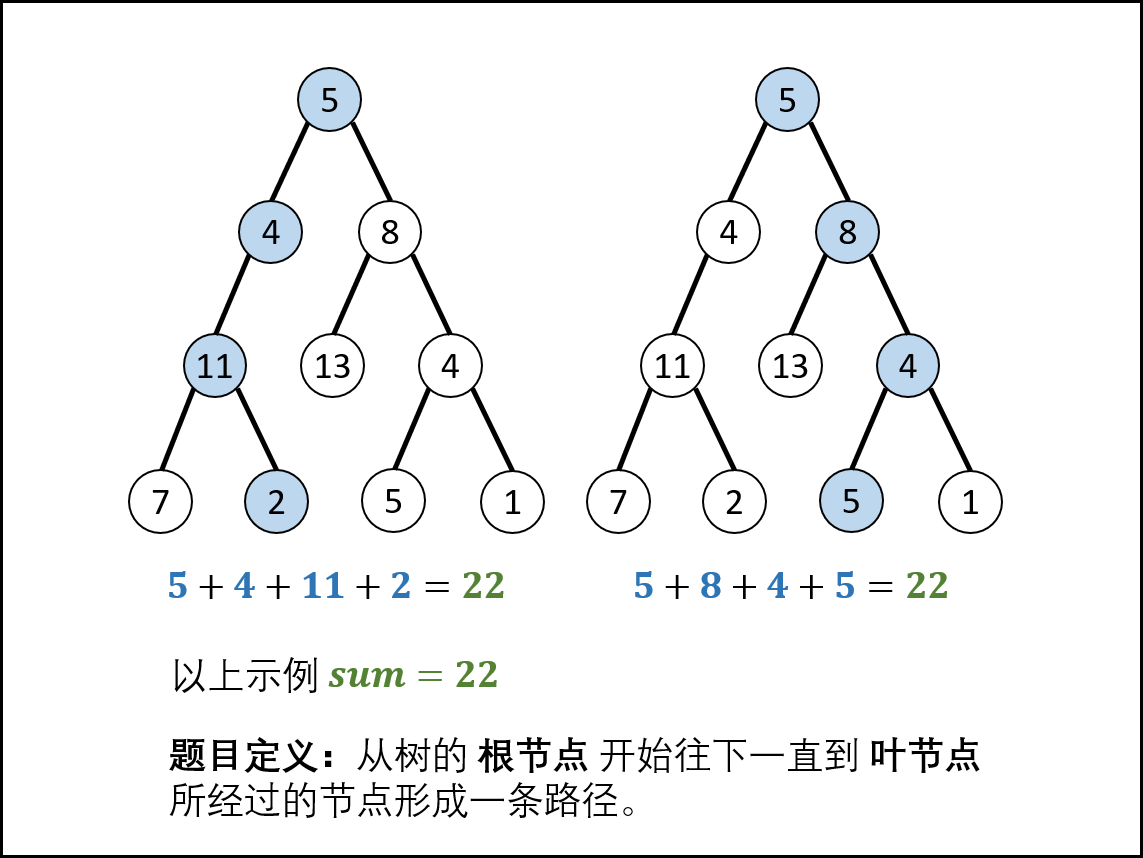
采用深度优先搜索的方式，枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点数。

• 空间复杂度 : $O(n)$

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;

    vector<vector<int>> pathSum(TreeNode* root, int target) {
        dfs(root, 0, target);
        return res;
    }

    void dfs(TreeNode* root, int sum, int target) {
        if (!root) return;

        path.push_back(root->val);
        sum += root->val;
        if (!root->left && !root->right) {
            if (sum == target) res.push_back(path);
        } else {
            if (root->left) dfs(root->left, sum, target);
            if (root->right) dfs(root->right, sum, target);
        }

        path.pop_back();
    }
};

---