三个例题说明白什么是回溯算法，javascript解决组合问题

最近忙疯了呜呜呜，读研不易，小李叹气…
今天好不容易忙的差不多了，刷了一会力扣，最近在刷回溯算法，刷着刷着还是觉得有点难，总结一波~

什么是回溯算法

回溯算法其实很复杂，本质上就是一种穷举的方式，穷举所有可能的结果，然后选出我们想要的答案。

怎么理解呢，其实我们一般在组合数中用回溯算法比较多，比如，从N个数里面按照一定的规则找出k个数的集合，这种问题我们就可以用到回溯算法。

具体怎么用呢？我们在解决组合问题的时候，往往会构造一棵树，然后一层层去遍历，回溯算法就是在集合中递归查找子集，集合的大小就是树的宽度，子集的大小就是数的深度；

看到这里可能还是有点懵┭┮﹏┭┮，下面通过案例来讲解：

案例1：力扣第77题.组合

题目是这样的：

其实这个题就是一个典型的组合问题，从n个数中抽取k个数，组成集合，只不过我们要列举出来所有的集合情况，“列举所有的情况”，遇到这种，一般肯定就是穷举，用for循环肯定也能解决，但是如果n和k的值一旦变得很大，for循环就很冗余和复杂，所以这里最好学会使用回溯。

根据上面介绍的，回溯法就是构建一棵树，宽度为n，深度为k,这里假设n为4，k为2,就可以画出树形结构如下所示：

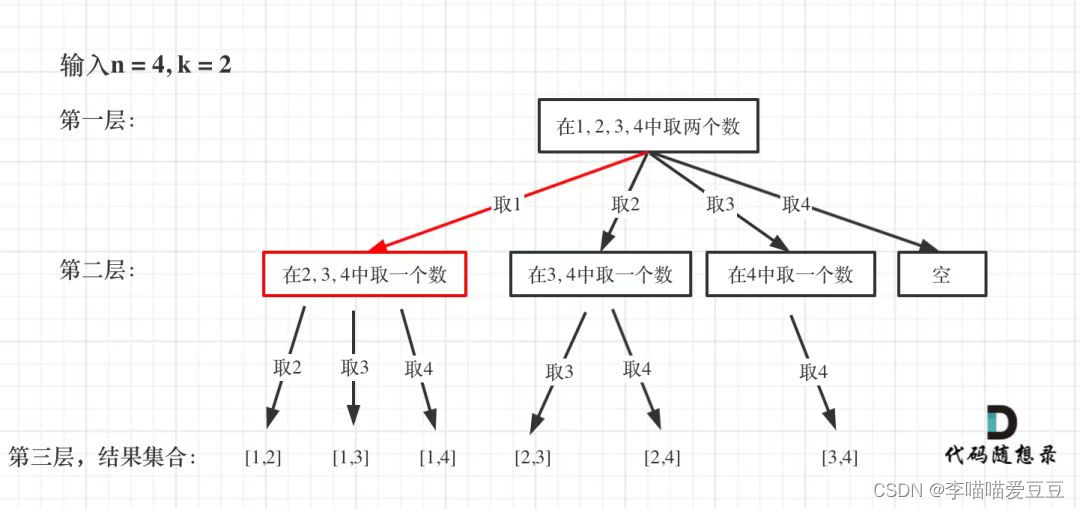
其实这个图就很清晰明了啦，其实问题就转换成，树的遍历问题，把从root节点到最后的子节点的所有路径都写出来，现在关键是怎么写代码，先把正确的代码摆出来：

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function(n, k) {
    var result=[];//这个定义了全局变量，用来保存最终结果的
    var path=[];//这个定义了全局变量，用来保存树的每一条路径
    var temp=[]//这里注意坑，这里我采用一个中间变量来承接path的内容，不然直接=赋值的就是数组的地址,可以敲代码验证一下
    //----------------这个函数就是定义的的递归函数————————————————
    var backtracking=function(n,k,index){
        if(path.length==k){//定义递归跳出的最终条件
            for(var i=0;i<k;i++){
              temp.push(path[i]);
            } 
            result.push(temp)  
            temp=[]  
            return;
        }
        for(var i=index;i<=n;i++){//控制树的横向遍历
            path.push(i);//处理节点
            backtracking(n,k,i+1);//控制树的纵向遍历
            path.pop();//回溯，撤销处理的节点
        }
    }
    backtracking(n,k,1);
    return result;
};

具体的写在注释里面啦，建议多看几遍代码结构，后面好几个题都要这样写~

看懂上面这个题之后，下面通过几个题目练练手，也是用到了回溯算法，看看能否举一反三：

案例2：力扣216.组合总和III

画图是这样的（这里举k=2,n=4的例子）：

其实这个题本质上和上一个题差不多，就是从9个数中选出k个数的集合,上一题中递归结束的条件是path数组的长度等于k，这里结束的条件稍微发生了变化，首先path数组的长度也要等于k，其次，这k个数的和应该等于n。想到这里，其实就很容易照着上面写出代码：

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function(n, k) {
    var result=[];
    var path=[];
    var temp=[];
    //更改点1
    var sum=0;
    var backtracking=function(n,k,index){
        if(path.length==k){
        	if(sum==n){//更改点2
            for(var i=0;i<k;i++){
              temp.push(path[i]);
            } 
            result.push(temp)  
            temp=[] } 
            return;
        }
        for(var i=index;i<=9;i++){//更改点3
            path.push(i);
            sum=sum+i;//更改点4
            backtracking(n,k,i+1);
            path.pop();
            sum=sum-i;//更改点5
        }
    }
    backtracking(n,k,1);
    return result;
};

这样问题就完美的解决了~下面我们继续加大点难度，这次我们尝试不要复制上面的代码，尝试自己去手敲：

案例3：力扣17.电话号码的字母组合

其实这个题还是和之前的问题一样，只是现在这个n不确定，n=digits.length*3,digits.length对应的就是输入的数字的个数，每个数字除了0和1，都代表三个字母。k等于digits.length。所以我们可以考虑用一个数组来保存每个数字对应的字母：

/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function(digits) {
    const letterMap=["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];
    var result=[];
    var path=[];
    var temp=[];
    var backtracking=function(digits,index){
        if(path.length==digits.length){
            for(var i=0;i<path.length;i++){
                temp.push(path[i]);
            }
            result.push(temp.join(''));
            temp=[];
            return;
        }
        var digit=digits[index]-0;
        var letters=letterMap[digit];
        for( var j=0;j<letters.length;j++){
            path.push(letters[j]);
            backtracking(digits,index+1);
            path.pop();
        }
    }
    if(digits.length==0){
        return result;
    }
    backtracking(digits,0);
    return result;
};

这个题的区别在于，怎么把上一层和下一层区分开来，之前都是通过加1进行区分，现在是对字母进行遍历，还是有点难度的。