Efficient Programming
“An engineer will do for a dime what any fool will do for a dollar” – Paul Hilfinger
编程的效率取决于以下两方面因素:
- 编程时的消耗(programming cost)
- 你花费多长时间编写好程序?
- 你的代码是否易读、是否易于更改、易于维护?
- 运行时的消耗(Execution cost)
- 你的程序将会执行多长时间
- 你的程序将会占用多大内存空间
Programming cost
我们首先来了解一组概念。
API (Application Programming Interface) 是一些预先定义的方法,每个方法都有简短的描述。
ADT (Abstract Data Structures) 是具有类似行为的高级数据类型。
比如,在 Proj1a 中,Deque 有具体的相似的行为(addFirst, addLast 等),而且我们使用的是它的实现类 ArrayDeque 和 LinkedListDeque 所以它是一个 ADT。
一些 ADT 是 其他 ADT 的特殊情况。比如,Stacks 和 Queues 就定义了更具体的行为,而它们仍然是 ADT。
接下来做一个小练习。
使用 Linked List 实现一个 Stack 类,并实现 push(Item x) 方法,确保这个类支持泛型。
下面给出三种常见的实现方法:
public class ExtensionStack<Item> extends LinkedList<Item> {
public void push(Item x) {
add(x);
}
}
这种方法通过 继承 实现,简单的调用了 LinkedList<Item> 中的方法。
public class DelegationStack<Item> {
private LinkedList<Item> L = new LinkedList<Item>();
public void push(Item x) {
L.add(x);
}
}
这种方法通过委托(Delegation) 实现,它在类的内部创造了一个 Linked List 的对象,然后调用它的方法完成目标。
public class StackAdapter<Item> {
private List L;
public StackAdapter(List<Item> worker) {
L = worker;
}
public void push(Item x) {
L.add(x);
}
}
这种方法和上一种类似,只不过它可以支持 List 接口的任意实现类。
Delegation vs Extension
通过刚才的练习,我们发现 Delegation 和 Extension 似乎可以相互转换,但实际上它们之间有一些值得关注的不同之处。
Extension 使用前必须清楚父类中发生了什么,换句话说,你必须知道父类的方法是怎样实现的。而使用 Delegation 时,你不需要把当前类认为是父类的一个新的版本,父类的对象只是一个工具而已。
Asymptotic
1. Introduction to Asymptotic Analysis
我们先解决一个问题:如何确定一个数组中含有两个相同的数?
似乎有两种解决方案:
- Silly Algorithm:
每两个数字之间进行比较,如果相等则返回 true - Better Algorithm: 好好利用数组的
排序算法
下面我们根据上述两个思路依次实现
//Silly Duplicate: compare everything
public static boolean dup1(int[] A) {
for (int i = 0; i < A.length; i += 1) {
for (int j = i + 1; j < A.length; j += 1) {
if (A[i] == A[j]) {
return true;
}
}
}
return false;
}
//Better Duplicate: compare only neighbors
public static boolean dup2(int[] A) {
for (int i = 0; i < A.length - 1; i += 1) {
if (A[i] == A[i + 1]) {
return true;
}
}
return false;
}
比较两种方法的运行速度,我们有以下几种方法:
- 使用客户端的程序测量运行速度
比较低级的方法是用秒表测量;如果使用 Unix 系统的话,可以使用 time 命令测量;或者可以使用 Princeton Standard 的库,里面有一个 stopwatch 类同样可以测量。
结果表明,当我们输入的数组越大时,dup1 将花费更长的时间执行程序,而 dup2 的运行时间几乎没有什么变化。
优点: 简单方便
缺点: 可能会耗费很多时间测试,而且在不同的操作系统、编译器上运行结果也会不同。
- 计算程序执行过程中各个操作的数量
下面是两种方法的统计结果
dup1
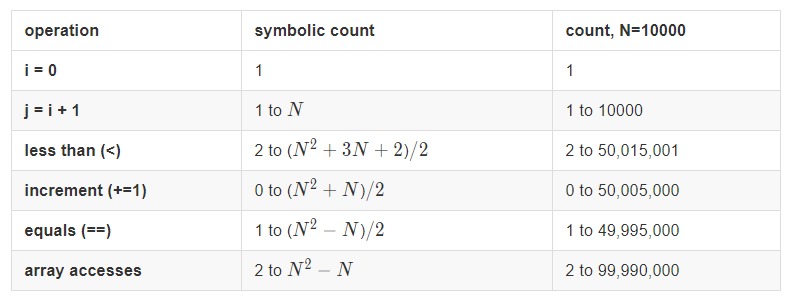
dup2

显然,完成同样的目标 dup2 进行了更少的操作,所以 dup2 方法更佳。
优点: 不受计算机构造的干扰,并且形成了一定的数学模型
缺点: 计算的过程太复杂,而且没有显示程序运行时间
并且,通过上述方法我们可以总结出计算算法时间复杂度的一般步骤:
- 只考虑最差的情况(即操作次数的幂最大)
- 在众多操作中选择一个有代表性的操作
Good choice:
increment, or less than or equals or array accesses
Bad choice: ssignment of j= i + 1, or i = 0
- 忽略幂数较低的部分
- 忽略常系数
根据以上四个步骤可以得到 dup2 的时间复杂度是 N,dup1 的时间复杂度是 N^2
下面做一个练习熟悉简化的过程





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










