L2正则化（Regularization）

正则化（Regularization）

深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差,下面我们就来讲讲正则化的作用原理。

我们用逻辑回归来实现这些设想，求成本函数$J$的最小值，它是我们定义的成本函数，参数包含一些训练数据和不同数据中个体预测的损失，$w$和$b$是逻辑回归的两个参数，$w$是一个多维度参数矢量，$b$是一个实数。在逻辑回归函数中加入正则化，只需添加参数λ，也就是正则化参数，一会儿再详细讲。

$\frac{\lambda }{2m}$乘以$w$范数的平方，其中${\Vert w\Vert }_2^2$是$w$的欧几里德范数的平方，等于$w_j$（$j$ 值从1到$n_x$）平方的和，也可表示为$w^{T}w$，也就是向量参数$w$ 的欧几里德范数（2范数）的平方，此方法称为$L2$正则化，因为这里用了欧几里德范数，被称为向量参数$w$的$L2$范数。

为什么只正则化参数$w$？为什么不再加上参数 $b$ 呢？你可以这么做，只是我习惯省略不写，因为$w$通常是一个高维参数矢量，已经可以表达高偏差问题，$w$可能包含有很多参数，我们不可能拟合所有参数，而$b$只是单个数字，所以$w$几乎涵盖所有参数，如果加了参数$b$，其实也没太大影响，因为$b$只是众多参数中的一个，所以我通常省略不计，如果你想加上这个参数，完全没问题。

$L2$正则化是最常见的正则化类型，你们可能听说过$L1$正则化，$L1$正则化，加的不是$L2$范数，而是正则项$\frac{\lambda }{m}$乘以${\sum }_{j=1}^{n_x}|w|$，${\sum }_{j=1}^{n_x}|w|$也被称为参数$w$向量的$L1$范数，无论分母是$m$还是$2m$，它都是一个比例常量。

如果用的是$L1$正则化，$w$最终会是稀疏的，也就是说$w$向量中有很多0，有人说这样有利于压缩模型，因为集合中参数均为0，存储模型所占用的内存更少。实际上，虽然$L1$正则化使模型变得稀疏，却没有降低太多存储内存，所以我认为这并不是$L1$正则化的目的，至少不是为了压缩模型，人们在训练网络时，越来越倾向于使用$L2$正则化。

我们来看最后一个细节，$\lambda$是正则化参数，我们通常使用验证集或交叉验证集来配置这个参数，尝试各种各样的数据，寻找最好的参数，我们要考虑训练集之间的权衡，把参数设置为较小值，这样可以避免过拟合，所以λ是另外一个需要调整的超级参数，这就是在逻辑回归函数中实现$L2$正则化的过程，如何在神经网络中实现$L2$正则化呢？

神经网络含有一个成本函数，该函数包含$W^{[1]}$，$b^{[1]}$到$W^{[l]}$，$b^{[l]}$所有参数，字母$L$是神经网络所含的层数，因此成本函数等于$m$个训练样本损失函数的总和乘以$\frac{1}{m}$，正则项为$\frac{\lambda }{2m}{{\sum }_1^L|W^{[l]}|}^2$，我们称${||W^{\left[l\right]}||}^2$为范数平方，这个矩阵范数${||W^{\left[l\right]}||}^2$（即平方范数），被定义为矩阵中所有元素的平方求和，

我们看下求和公式的具体参数，第一个求和符号其值$i$从1到$n^{[l-1]}$，第二个其$J$值从1到$n^{[l]}$，因为$W$是一个$n^{[l]}\times n^{[l-1]}$的多维矩阵，$n^{[l]}$表示$l$ 层单元的数量，$n^{[l-1]}$表示第$l-1$层隐藏单元的数量。

该矩阵范数被称作“弗罗贝尼乌斯范数”，用下标$F$标注”，鉴于线性代数中一些神秘晦涩的原因，我们不称之为“矩阵$L2$范数”，而称它为“弗罗贝尼乌斯范数”，矩阵$L2$范数听起来更自然，但鉴于一些大家无须知道的特殊原因，按照惯例，我们称之为“弗罗贝尼乌斯范数”，它表示一个矩阵中所有元素的平方和。

该如何使用该范数实现梯度下降呢？

用backprop计算出$dW$的值，backprop会给出$J$对​$W$的偏导数，实际上是​$W^{[l]}$，把​$W^{[l]}$替换为​$W^{[l]}$减去学习率乘以​$dW$。

这就是之前我们额外增加的正则化项，既然已经增加了这个正则项，现在我们要做的就是给$dW$加上这一项$\frac{\lambda }{m}{W}^{[l]}$，然后计算这个更新项，使用新定义的$d{W}^{[l]}$，它的定义含有相关参数代价函数导数和，以及最后添加的额外正则项，这也是$L2$正则化有时被称为“权重衰减”的原因。

我们用$d{W}^{[l]}$的定义替换此处的$d{W}^{[l]}$，可以看到，$W^{[l]}$的定义被更新为$W^{[l]}$减去学习率$\alpha$ 乘以backprop 再加上$\frac{\lambda }{m}{W}^{[l]}$。

该正则项说明，不论$W^{[l]}$是什么，我们都试图让它变得更小，实际上，相当于我们给矩阵W乘以$(1-\alpha \frac{\lambda }{m})$倍的权重，矩阵$W$减去$\alpha \frac{\lambda }{m}$倍的它，也就是用这个系数$(1-\alpha \frac{\lambda }{m})$乘以矩阵$W$，该系数小于1，因此$L2$范数正则化也被称为“权重衰减”，因为它就像一般的梯度下降，$W$被更新为少了$\alpha$乘以backprop输出的最初梯度值，同时$W$也乘以了这个系数，这个系数小于1，因此$L2$正则化也被称为“权重衰减”，以上就是在神经网络中应用$L2$正则化的过程。

为什么正则化有利于预防过拟合呢？（Why regularization reduces overfitting?）

为什么正则化有利于预防过拟合呢？为什么它可以减少方差问题？我们通过两个例子来直观体会一下。

左图是高偏差，右图是高方差，中间是**Just Right**

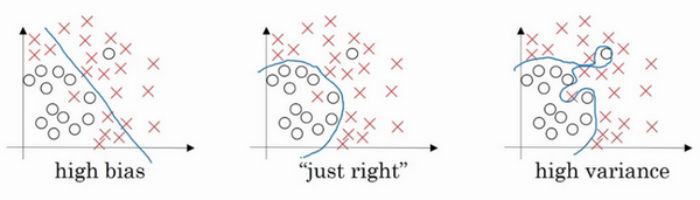
现在我们来看下这个庞大的深度拟合神经网络。我知道这张图不够大，深度也不够，但你可以想象这是一个过拟合的神经网络。这是我们的代价函数$J$，含有参数$W$，$b$。我们添加正则项，它可以避免数据权值矩阵过大，这就是弗罗贝尼乌斯范数，为什么压缩$L2$范数，或者弗罗贝尼乌斯范数或者参数可以减少过拟合？

直观上理解就是如果正则化$\lambda$设置得足够大，权重矩阵$W$被设置为接近于0的值，直观理解就是把多隐藏单元的权重设为0，于是基本上消除了这些隐藏单元的许多影响。如果是这种情况，这个被大大简化了的神经网络会变成一个很小的网络，小到如同一个逻辑回归单元，可是深度却很大，它会使这个网络从过度拟合的状态更接近左图的高偏差状态。

但是$\lambda$会存在一个中间值，于是会有一个接近“Just Right”的中间状态。

直观理解就是$\lambda$增加到足够大，$W$会接近于0，实际上是不会发生这种情况的，我们尝试消除或至少减少许多隐藏单元的影响，最终这个网络会变得更简单，这个神经网络越来越接近逻辑回归，我们直觉上认为大量隐藏单元被完全消除了，其实不然，实际上是该神经网络的所有隐藏单元依然存在，但是它们的影响变得更小了。神经网络变得更简单了，貌似这样更不容易发生过拟合，因此我不确定这个直觉经验是否有用，不过在编程中执行正则化时，你实际看到一些方差减少的结果。

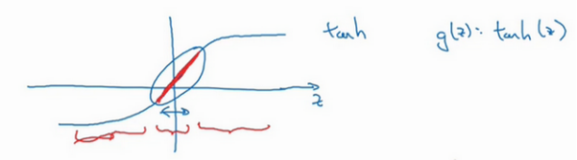
我们再来直观感受一下，正则化为什么可以预防过拟合，假设我们用的是$tanh$这样的双曲线激活函数。

用$g(z)$表示$tanh(z)$，我们发现如果 z 非常小，比如 z 只涉及很小范围的参数（图中原点附近的红色区域），这里我们利用了双曲正切函数的线性状态，只要$z$可以扩展为这样的更大值或者更小值，激活函数开始变得非线性。

如果正则化参数λ很大，激活函数的参数会相对较小，如果$W$很小，相对来说，$z$也会很小。

特别是，如果$z$的值最终在这个范围内，都是相对较小的值，$g(z)$大致呈线性，每层几乎都是线性的，和线性回归函数一样。

如果每层都是线性的，那么整个网络就是一个线性网络，即使是一个非常深的深层网络，因具有线性激活函数的特征，最终我们只能计算线性函数，因此，它不适用于非常复杂的决策，以及过度拟合数据集的非线性决策边界，如同我们上面看到的过度拟合高方差的情况。

总结一下，如果正则化参数变得很大，参数$W$很小，$z$也会相对变小，此时忽略$b$的影响，$z$会相对变小，实际上，$z$的取值范围很小，这个激活函数，也就是曲线函数$tanh$会相对呈线性，整个神经网络会计算离线性函数近的值，这个线性函数非常简单，并不是一个极复杂的高度非线性函数，不会发生过拟合。

这就是$L2$正则化，它是我在训练深度学习模型时最常用的一种方法。