C语言取整（含强制转换）

约定：

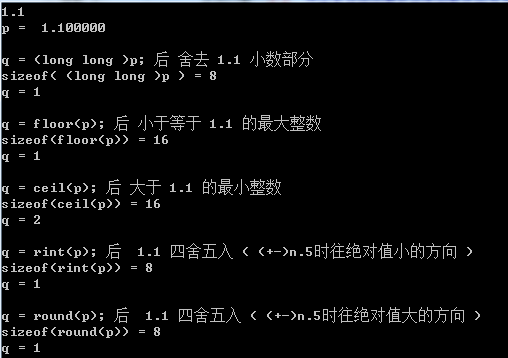
	long double p;
	long long q;

0 应用于

https://blog.youkuaiyun.com/qq_40893824/article/details/105907220 1.3 节

1 浮点数取整

1.1 强制转换

	q = (long long )p;

1.2 函数

1.2.1floor()

	q = floor(p);

1.2.2 ceil()

	q = ceil(p);

1.2.3 rint()

	q = rint(p);

1.2.4 round()

	q = round(p);

1.3 验证代码

#include<bits/stdc++.h> 
using namespace std;

int main()
{
	long double p;
	long long q;
	scanf("%Lf", &p);
	while(1)
	{
		getchar(); 
		printf("p = % Lf\n\n", p) ;
		
		//1 (long long) 强制转换 取整 舍去小数部分 
		cout << "q = (long long )p; 后 舍去 " << p << " 小数部分" << endl;
		q = (long long )p;
		cout << "sizeof( (long long )p ) = "  << sizeof((long long )p) << endl; 
		printf("q = %lld\n\n", q);
		
		//2 floor(p) 强制转换 取整 小于等于 x的最大整数 返回double型
		cout << "q = floor(p); 后 小于等于 " << p << " 的最大整数" << endl;
		q = floor(p);
		cout << "sizeof(floor(p)) = "  << sizeof(floor(p)) << endl;
		printf("q = %lld\n\n", q);
		
		//3 ceil(p) 强制转换 取整 大于x的最小整数 返回double型
		cout << "q = ceil(p); 后 大于 " << p << " 的最小整数" << endl;
		q = ceil(p);
		cout << "sizeof(ceil(p)) = "  << sizeof(ceil(p)) << endl;
		printf("q = %lld\n\n", q);
		
		//4 rint(p) 强制转换 取整 四舍五入 (+-)n.5时往绝对值小的方向 
		cout << "q = rint(p); 后  "<< p << " 四舍五入 ( (+-)n.5时往绝对值小的方向 )" << endl;
		q = rint(p);
		cout << "sizeof(rint(p)) = "  << sizeof(rint(p)) << endl;
		printf("q = %lld\n\n", q);
		
		//4 round(p) 强制转换 取整 四舍五入 (+-)n.5时往绝对值小的方向 
		cout << "q = round(p); 后  "<< p << " 四舍五入 ( (+-)n.5时往绝对值大的方向 )" << endl;
		q = round(p);
		cout << "sizeof(round(p)) = "  << sizeof(round(p)) << endl;
		printf("q = %lld\n\n\n", q);
		
		scanf("%Lf", &p);
	}
	system("pause");
	return 0;
}

返回类型 用 sizeof() 判断：

1.4 总结

	使用形式	做法	返回
强制转换	(数据类型)p	去小数部分	整数
函数	floor(p)	小于等于 p的最大整数	整数
ceil(p)	大于p的最小整数	浮点数double
rint(p)	四舍五入，(+-)n.5时往绝对值小的方向	浮点数double
round(p)	四舍五入，(+-)n.5时往绝对值小的方向	整数

2 整数取整

结论：
在0 < M <= N， M, N∈Z 时，int nn = (N-1) / M +1，其中 除法 ‘/’ 往下取整

推导：

设N = Mk + r (0 <= r < M，k∈Z)
< > 向上取整，[ ] 向下取整

当 r > 0
左：< N / M > = < ( Mk + r ) / M >= < k + r / M >= k + < r / M > = k+1
右：[ (N - 1) / M ] + 1 = [ (Mk + r - 1) / M ] + 1 = [ k + (r - 1) / M ] + 1 = k+1+[ (r - 1) / M ] = k + 1

当 r = 0
左：< N / M > = k
右：[ (N - 1) / M ] + 1 = [ (Mk - 1) / M ] + 1 = [ ( M(k - 1) + M - 1 ) / M ] + 1
= [ k - 1 + (M - 1) / M ] + 1 = k + [ (M - 1) / M ]
= k