深度学习理论基础9-多维数组

>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A)    #这个方法返回np数组的维度
1
>>> A.shape   #这个属性返回这个np数组的形状。也就是每个维度的元素数量。始终返回一个元组
(4,)

--------二维数组----

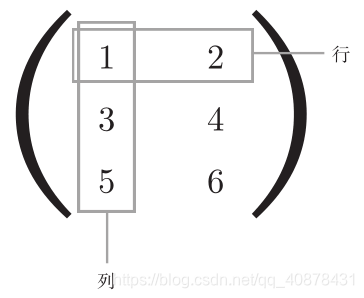
二维数组也称为矩阵。数组的横向排列称为行（row），纵向排列称为列（column）。

--------矩阵乘法--------

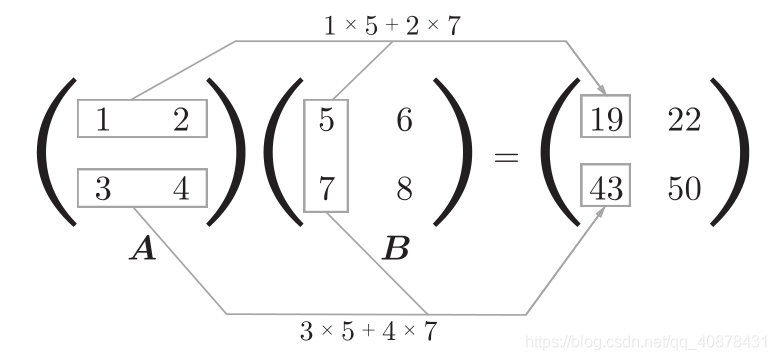
np.dot(A, B)   --->矩阵乘法的运算使用这个方法

A的行与B的列相乘后相加。

所以A的行与B的列必须等长！！

否则它会报错给你看。矩阵乘法的长度变化应该是这样的mk*kn=mn。下面有一只图像快马加鞭赶过来帮助你理解。

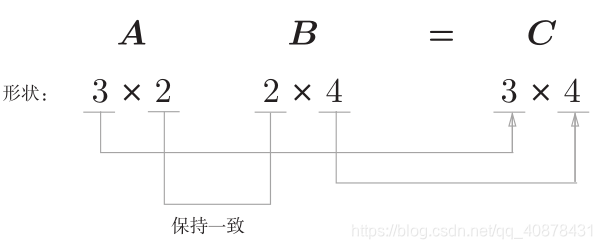
如果你依然感到迷惑，应该停下来，仔细想想，或者拿笔画一下。如果你准备好了，继续接受后面的知识。

--------矩阵乘法在神经网络中的应用--------

 

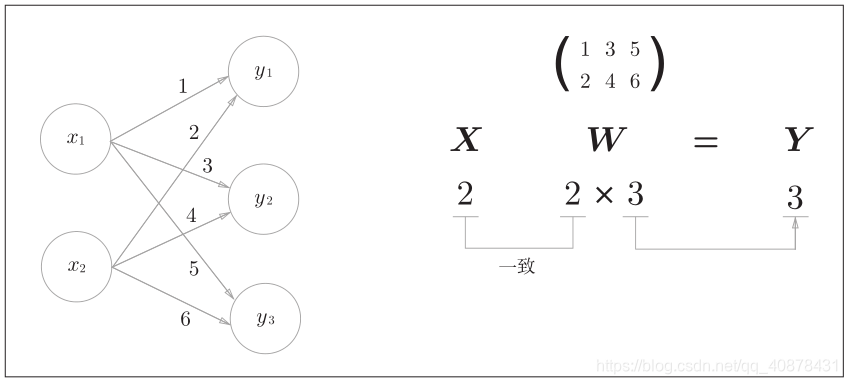
为了避免干扰，这个神经网络模型，仅展示了输入与权重相乘的部分。

图像只是为了形象化的理解。但实际运算还是得靠np数组。上图可能真实的样子是这样的：

A=np.array([1,2])
B=np.array([[0.5,0.3,0.8],[0.75,0.9,0.1]])
a=np.dot(A,B)

可以看到。通过numpy矩阵的乘积使神经网络的实现变的及其简单。

谨记，输入与权重的形状，必须遵守上面几幅图中的规则。

--------结语--------

本节主要说了矩阵的乘积。下一节会把方法运用到实践，通过矩阵积乘及激活函数实现一个3层神经网络(傻的)。