本次任务是周志华老师《机器学习》第六章支持向量机的内容,个人觉得本章是截至目前所有章节任务中难度相对最大且花时间最多的部分,也看了不少资料(还有一部分还没看完)。目前对SVM学习过程中花费时间最多去思考的一个问题——超平面函数间隔设置为1进行整理。
首先给出需要用到的数学表达式和符号:
样本集![]() ,
,![]() 线性可分;
线性可分;
![]() 是一个能够将正负样本恰好隔开的超平面,并且使得正样本在分隔超平面“上方”,负样本在分隔超平面“下方”,即对于正、负样本点分别有
是一个能够将正负样本恰好隔开的超平面,并且使得正样本在分隔超平面“上方”,负样本在分隔超平面“下方”,即对于正、负样本点分别有![]() 、
、![]() ,其中x+、x-分别表示正、负样本点;
,其中x+、x-分别表示正、负样本点;
正负样本对应的标记值为y+=1,y-=-1,即![]() ;
;
由此可知,当超平面分类正确时有![]() ,为便于公式推导和文字叙述,我们将
,为便于公式推导和文字叙述,我们将![]() 称为函数间隔;记
称为函数间隔;记![]() 为几何间隔,表示样本点到超平面的距离。
为几何间隔,表示样本点到超平面的距离。
在SVM算法中,对于线性可分的样本集,我们需要在众多超平面中寻找出最优的那个,即找到离超平面最近的样本点与超平面的几何间隔最大的一个。最大间隔超平面需要满足两个约束条件:一是能够将正负样本正确分类;二是离超平面最近的样本点与超平面的几何间隔最大。
第一个条件即前文所述![]() ,所以主要分析第二个条件。由于样本点数据已知,所以最小几何间隔是关于
,所以主要分析第二个条件。由于样本点数据已知,所以最小几何间隔是关于和b的函数,用d(
,b)来表示,来表示,由于
与i无关,所以可以将其提出放在最小化式子前面。接下来我们改变超平面的法向量方向和截距,即改变
和b,在最小几何间隔的所有变化值的集合中,寻找最大的那个值以及相应的
和b。
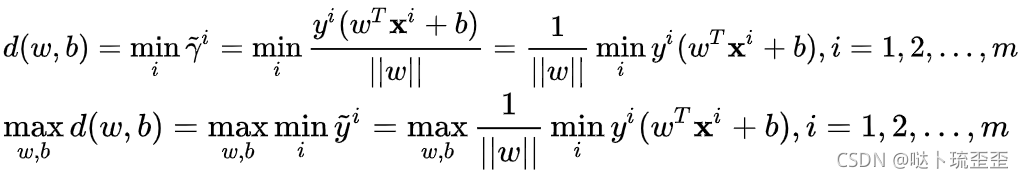
结合这两个约束条件,得最大间隔超平面的求解公式:
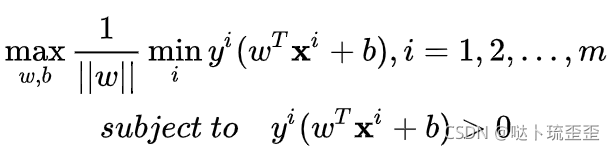
下面对该式进行化简。
将![]() 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/8b20d27fdc04767b453faf802d174f5f.png) 表示原超平面的
表示原超平面的![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) ,
,和
表示变化后的超平面的
![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) 。变化前的超平面为
。变化前的超平面为![[公式]](https://i-blog.csdnimg.cn/blog_migrate/4f3a63cdd97374e4575247c16ec66aa1.png%5ETx%2Bb_k%3D0) ,变化后的超平面为
,变化后的超平面为![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png%5ET_%7Bk%2B1%7Dx%2Bb_%7Bk%2B1%7D%3D0) 。
。
当等比例变化时,变化后的超平面与变化前的超平面相同,即
![]()
以下图为例,三个表达式中的![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) 虽然不同,但对应成比例,所以表示的是同一条直线。拓展到超平面上,可以说某一确定的超平面对应无数个
虽然不同,但对应成比例,所以表示的是同一条直线。拓展到超平面上,可以说某一确定的超平面对应无数个![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) 。
。

如果不将这个缩放对超平面表达式的影响消除的话,那么解出的最优超平面也对应有无数个![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) ,解不唯一。 故需要添加限制条件使得对应的
,解不唯一。 故需要添加限制条件使得对应的![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) 是唯一的,SVM选用的限制条件为:
是唯一的,SVM选用的限制条件为:
![]()
当超平面固定,即![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) 非等比例缩放时,一定能找到所有样本点中与超平面函数间隔最小的样本点,不妨将这个解记为
非等比例缩放时,一定能找到所有样本点中与超平面函数间隔最小的样本点,不妨将这个解记为![[公式]](https://i-blog.csdnimg.cn/blog_migrate/e54f3efd68112f38976b7b5b731ca610.png) 。在
。在![[公式]](https://i-blog.csdnimg.cn/blog_migrate/e54f3efd68112f38976b7b5b731ca610.png) 的数据值和超平面固定的条件下,令
的数据值和超平面固定的条件下,令![[公式]](https://i-blog.csdnimg.cn/blog_migrate/885afa9a48358cfed3dd351dceba2ad0.png) 就相当于自适应缩放固定超平面的某一个
就相当于自适应缩放固定超平面的某一个![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) ,以使得最终
,以使得最终![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png%2Cb) 代入
代入![[公式]](https://i-blog.csdnimg.cn/blog_migrate/56f74e6764390f8b6f062cac015fd03d.png) 结果为1。因此,限制条件
结果为1。因此,限制条件![]() 可以消除等比例缩放对解的影响,虽然无法得知离超平面最近的那个样本点具体是哪一个。此时,与超平面最近的点到超平面的距离,即最小几何间隔为
可以消除等比例缩放对解的影响,虽然无法得知离超平面最近的那个样本点具体是哪一个。此时,与超平面最近的点到超平面的距离,即最小几何间隔为
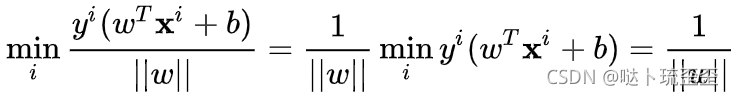
此时目标函数转化为:
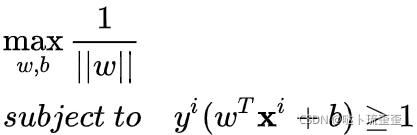
当![[公式]](https://i-blog.csdnimg.cn/blog_migrate/1c7a330b82678d6b033d9748f5120af9.png) 和
和![[公式]](https://i-blog.csdnimg.cn/blog_migrate/111cf5c2cf1cc54e0b93080ff933d2e8.png) 非等比例变化时,超平面的方向、方位就发生了变化,也就是对应上面的这个式子:
非等比例变化时,超平面的方向、方位就发生了变化,也就是对应上面的这个式子:
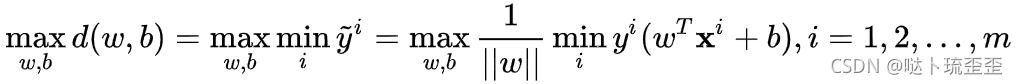
逐步改变超平面的方位,然后求超平面最小几何间隔;再逐步改变超平面方位,再求最小几何间隔……




 本文详细探讨了支持向量机中如何通过设置函数间隔为1,解决线性可分样本集的最大间隔超平面问题。通过数学公式推导,解释了如何消除等比例缩放对超平面的影响,以求得唯一最优解。关键步骤包括超平面方向调整和最小几何间隔计算。
本文详细探讨了支持向量机中如何通过设置函数间隔为1,解决线性可分样本集的最大间隔超平面问题。通过数学公式推导,解释了如何消除等比例缩放对超平面的影响,以求得唯一最优解。关键步骤包括超平面方向调整和最小几何间隔计算。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








