海浪谱

最新推荐文章于 2024-01-17 20:14:00 发布

王郁北辰

最新推荐文章于 2024-01-17 20:14:00 发布

阅读量7k

点赞数 5

文章标签：海浪谱

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/qq_40843083/article/details/102852035

版权

海浪谱（ocean wave spectrum）描述海浪内部能量相对于频率和方向分布的图谱。又称海洋能量谱，是研究海浪的重要概念。海浪谱不仅表明海浪内部构成，还能给出海浪的外部特征。

海浪可视作由无限多个振幅不同、频率不同、方向不同、位相杂乱的组成波组成，这些组成波便构成海浪谱。此谱描述海浪能量相对于各组成波的分布，故又名能量谱、功率谱、方向谱。它是随机海浪的一个重要统计性质，它不仅包含着海浪的二阶信息，而且还直接给出海浪组成波能量相对于频率和方向的分布。它用于描述海浪内部能量相对于频率和方向的分布。

海浪谱不仅表明海浪内部由哪些组成波构成，还能给出海浪的外部特征。比如，理论上可由谱计算各种特征波高和平均周期，利用这些特征量连同波高与周期的概率密度分布，可推算海浪外观上由哪些高低长短不同的波构成。若已知海浪的谱，海浪的内外结构都可得到描述，因此，谱是非常有用的概念。事实上，海浪的研究（包括许多应用问题），大多和谱有关。

从波面的记录估计谱，是获得海浪频谱的主要途径。习惯上将谱的估计方法分为相关函数法和快速傅氏变换算法两种。

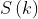海面功率谱函数主要表征了海浪在其频域内的波数分布情况，用 $S\left ( k \right )$ 或 $S\left ( \omega \right )$ 表示海面功率谱。它是波数或频率相关的函数，一般采用归一化的方式就功率谱进行具体的描述，即：

$\int_{0}^{\infty }S\left ( \omega \right )d\omega =\int_{0}^{\infty }S\left ( k \right )dk=\sigma ^{2}$

式中， $\sigma ^{2}$ 表示海浪某点相对于参考面的高度差， $\omega$ 是功率谱的频率，k代表波数。方向谱可以看成二维海面频谱，相比于一维功率谱，它增加了高度分量，这样便于描述海浪空间范围内的统计特性和能量特性。二维海浪谱的表现形式有 $S\left ( k_{x},k_{y} \right )$ 、 $s\left ( k,q \right )$ 和 $s\left ( \omega ,q \right )$ ； $\theta$ 是以X轴正方向为基准逆时针向参考方向所形成的夹角，如下图所示，式中 $k=\left ( kcos\theta ,ksin\theta \right )=\left ( k_{x},k_{y} \right )$ 。由此方向普与组成波振幅 $a_{n}$ 的关系为：

$S\left ( \omega,\theta\right )\delta \omega \delta \theta =\sum_{\omega }^{\omega +\delta \omega }\sum_{\theta }^{\theta +\delta \theta }\frac{1}{2}a_{n}^{2}$

式中等式右边的求和符号表示为对频率介于 $\omega$ 到 $\omega +\delta \omega$ 和方向且处于 $\theta$ 到 $\theta +\delta \theta$ 之间范围内组成波的算术和。

（方向谱角度示意图）

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。