PCA从原理到实践(基于R）

最新推荐文章于 2025-03-24 16:40:40 发布

生信小菜鸟啊

最新推荐文章于 2025-03-24 16:40:40 发布

阅读量2.3k

点赞数 4

分类专栏： R语言学习文章标签：可视化数据分析 pca降维

本文链接：https://blog.youkuaiyun.com/qq_40794743/article/details/109390664

版权

R语言学习专栏收录该内容

9 篇文章

订阅专栏

声明：
1、作者水平有限，不足之处请指正！
2、本文侧重于R中实现PCA分析。
3、#代表注释，##代表结果。

揭开PCA神秘面纱

1. 简介
2. PCA和可视化
参考

1. 简介

主成分是数据中的底层结构，是方差最大的方向，是数据分布最广的方向。这意味着当数据沿着这条直线投射时，可以找到那条最能分散数据的直线。这是第一个主成分，这条直线显示了数据中最实质性的变化。

PCA是对给定“宽”数据集进行的一种线性变换，该数据集具有一定数量的变量(坐标)和一定数量的空间值。线性转换将数据集匹配到一个新的坐标系统中，这样在第一个坐标上可以找到最显著的方差，并且随后的每个坐标都与最后一个正交，并且方差较小。通过这种方式，可以将y样本上的一组x相关变量转换为同一样本上的p组不相关主成分。

在许多变量相互关联的情况下，它们都对同一主成分有很大的贡献。每个主成分在数据集中的总变化中合计一定百分比。当初始变量相互之间具有很强的相关性时，能够用少量的主要成分来近似估计数据集中的大部分复杂性。当添加更多的主成分时，将总结越来越多的原始数据集。

PCA具体的原理请参考https://zhuanlan.zhihu.com/p/37777074.

2. PCA和可视化

R stats包提供了prcomp()和princomp()函数，gmodels包提供了fast.prcomp()函数来实现PCA分析。fast.prcomp()比stats包提供的函数快很多。我们使用mtcars数据集进行分析，因为PCA最适合于数值型数据，所以我们将vs和am变量删除，以剩下的数据作为本次的原始数据集进行PCA分析和可视化。

我们首先来比较一下这三种方法的差异。

library(gmodels)
library(tidyverse)
data <- mtcars %>% select(c(1:7,10,11))
da.prcomp <- prcomp(data)
da.princomp <- princomp(data)
da.fa.pca <- fast.prcomp(data)

输出数据类型

可以看到，prcomp()和fast.prcomp()输出都为prcomp对象，而princomp()输出对象是princomp，但是本质上都是list。

class(da.fa.pca)
# [1] "prcomp"
class(da.prcomp)
# [1] "prcomp"
class(da.princomp)
# [1] "princomp"

在这里插入图片描述

原理

具体参考简介。 princomp(）是通过对协方差矩阵求解特征值和特征向量来实现PCA分析；prcomp()和fast.prcomp()函数是通过SVD(奇异值分解）来实现PCA分析。从princomp()官方文档可知，其更推荐使用以SVD来实现PCA。

速度

prcomp()明显是比fast.prcomp()函数慢的，在这里就不做测试了。再说点题外话，它们产生的对象存在一定的不同，但对结果没影响。

所以，接下来我们使用fast.prcomp()函数来实现mtcars数据集的PCA分析。

1. 使用fast.prcomp()函数实现PCA，summary()，str()查看

library(gmodels)
library(tidyverse)
data <- mtcars %>% select(c(1:7,10,11))
da.fa.pca <- fast.prcomp(data,center = T,scale. = T)
summary(da.fa.pca)
##Importance of components:
##                          PC1    PC2     PC3     PC4     PC5     PC6
##Standard deviation     2.3782 1.4429 0.71008 0.51481 0.42797 0.35184
##Proportion of Variance 0.6284 0.2313 0.05602 0.02945 0.02035 0.01375
##Cumulative Proportion  0.6284 0.8598 0.91581 0.94525 0.96560 0.97936
                           PC7    PC8     PC9
##Standard deviation     0.32413 0.2419 0.14896
##Proportion of Variance 0.01167 0.0065 0.00247
##Cumulative Proportion  0.99103 0.9975 1.00000
str(da.fa.pca)
##List of 3
## $ sdev    : num [1:9] 2.378 1.443 0.71 0.515 0.428 ...
## $ rotation: num [1:9, 1:9] -0.393 0.403 0.397 0.367 -0.312 ...
##  ..- attr(*, "dimnames")=List of 2
##  .. ..$ : chr [1:9] "mpg" "cyl" "disp" "hp" ...
##  .. ..$ : chr [1:9] "PC1" "PC2" "PC3" "PC4" ...
## $ x       : num [1:32, 1:9] -0.664 -0.637 -2.3 -0.215 1.587 ...
##  ..- attr(*, "dimnames")=List of 2
##  .. ..$ : chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet ##4 Drive" ...
##  .. ..$ : chr [1:9] "PC1" "PC2" "PC3" "PC4" ...
## - attr(*, "class")= chr "prcomp"

$sdev表示标准偏差；$rotation表示初始变量与主成分之间的关系；$x表示每个样本的主成分值。

2. screenplot / plot和biplot简单可视化

screenplot()绘制了与主成分数量对应的方差。

screeplot(da.fa.pca) # 等于plot(da.fa.pca)
screeplot(da.fa.pca,type ="l") # 等于plot(da.fa.pca,type ="l")

在这里插入图片描述

biplot(da.fa.pca)

双图展示了样本的贡献值和样本之间的相似性，距离越近，越相似。
在这里插入图片描述

3. ggbiplot可视化

先来个初级的，只加了标签。

devtools::install_github("vqv/ggbiplot")
library(ggbiplot)
ggbiplot(da.fa.pca, labels=rownames(data))

在这里插入图片描述
我们为数据进行分组，设置ellipase参数为TRUE，再绘图。

# 分组
data.country <- c(rep("Japan", 3), rep("US",4), rep("Europe", 7),rep("US",3), "Europe", rep("Japan", 3), rep("US",4), rep("Europe", 3), "US", rep("Europe", 3))
# 绘图
ggbiplot(da.fa.pca,ellipse=TRUE,  labels=rownames(mtcars), groups=data.country)

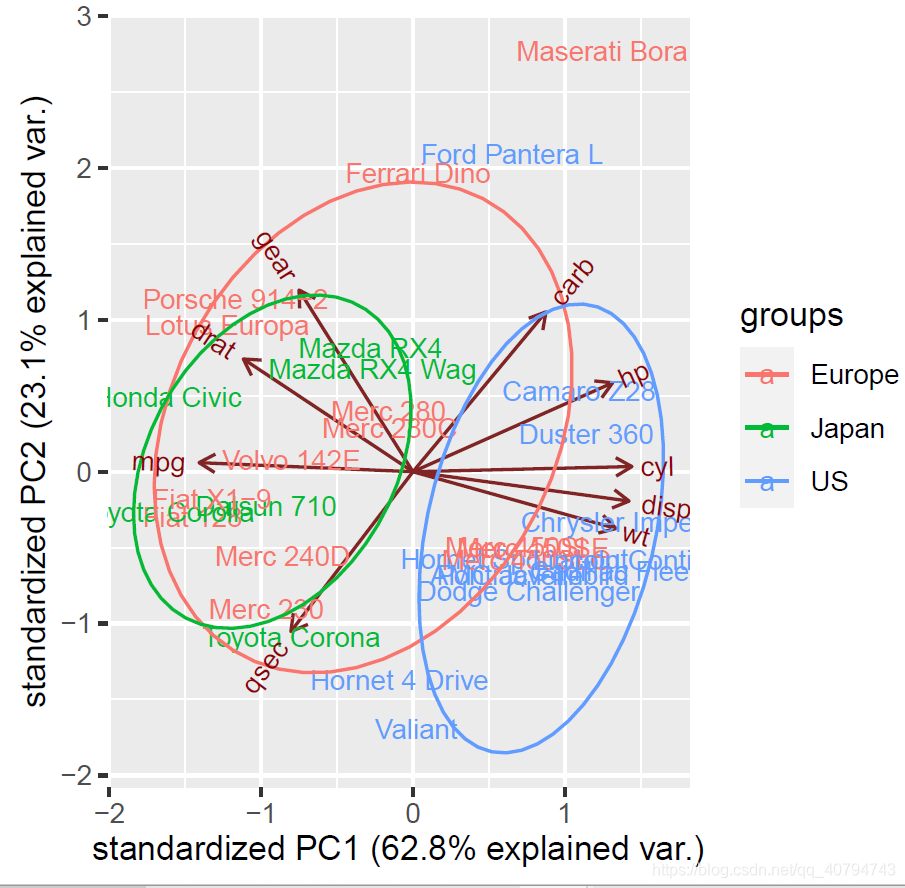
在这里插入图片描述
上面的图形看起来太乱了，不易读出有效信息。不过能看出PCA能很好地将将数据分为三组。美国汽车在右边形成了一个独特的集群。美国车的特点是cyl、disp和wt值高，而日本车的特点是mpg值高。欧洲车在某种程度上处于中间位置，与这两类车相比，它们的密集程度较低。

当然，你也可以使用PC3和PC4可视化，但是对我们一般的数据分析来说，PC1和PC2已经能够解释数据的绝大部分方差，所以没必要可视化PC3和PC4甚至其之后的主成分。

给图形加圈，去掉箭头。

ggbiplot(da.fa.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,  labels=rownames(mtcars), groups=data.country)
ggbiplot(da.fa.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,var.axes=FALSE,   labels=rownames(data), groups=data.country)

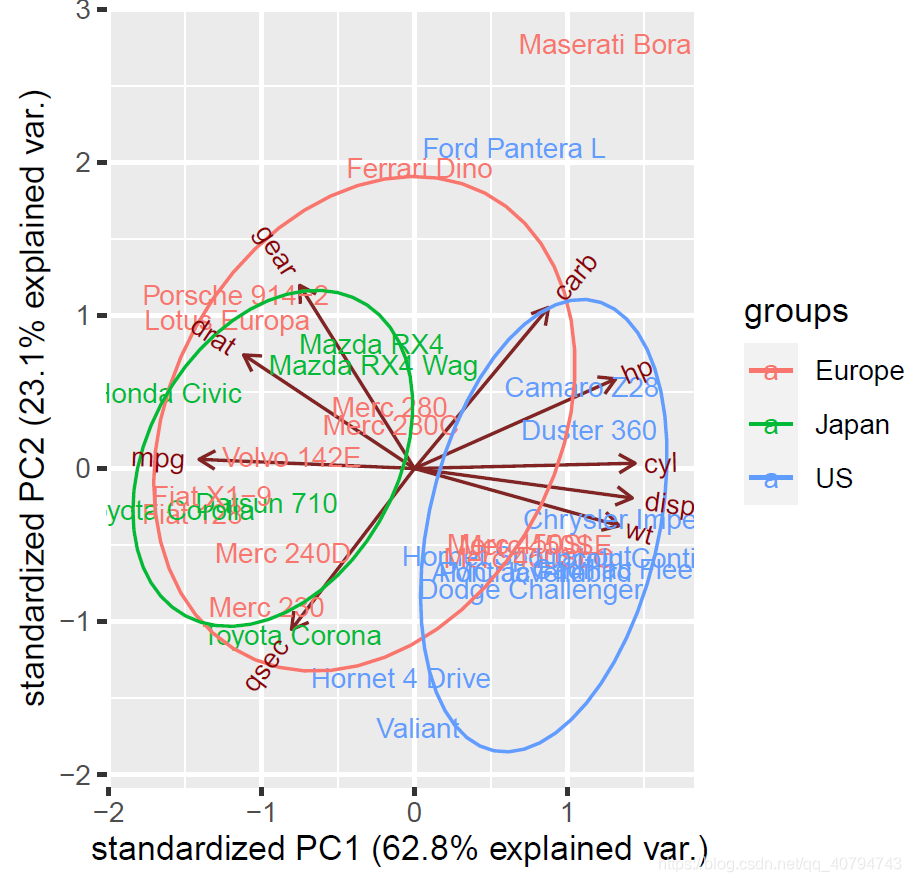
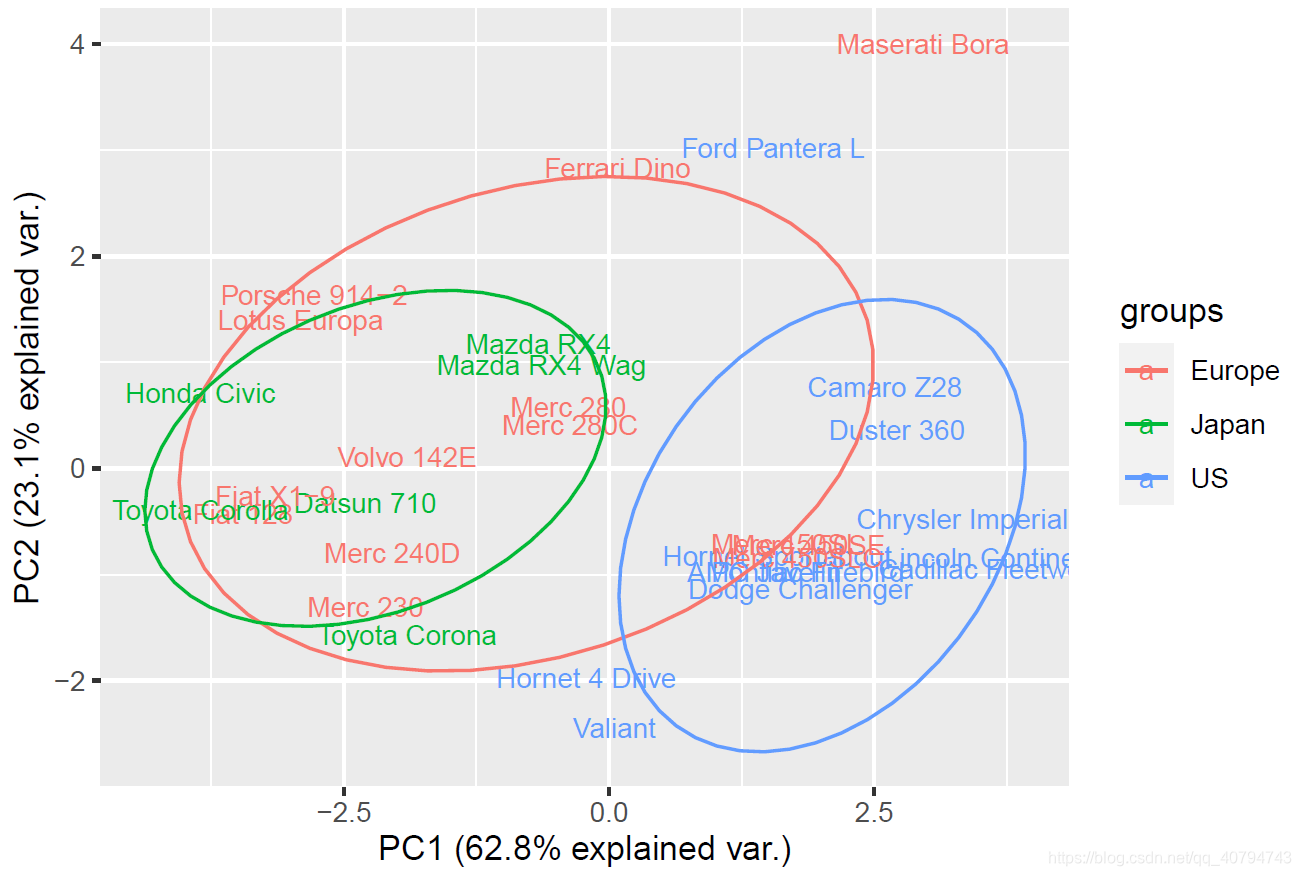
在这里插入图片描述

进一步美化，如果觉得标签碍眼，可以去掉。

library(ggsci)
ggbiplot(da.fa.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,  labels=rownames(data), groups=data.country) +
  scale_colour_aaas()+
  ggtitle("PCA of mtcars dataset")+
  theme_minimal()+
  theme(legend.position = "bottom")

在这里插入图片描述

# 去掉标签和箭头
library(ggsci)
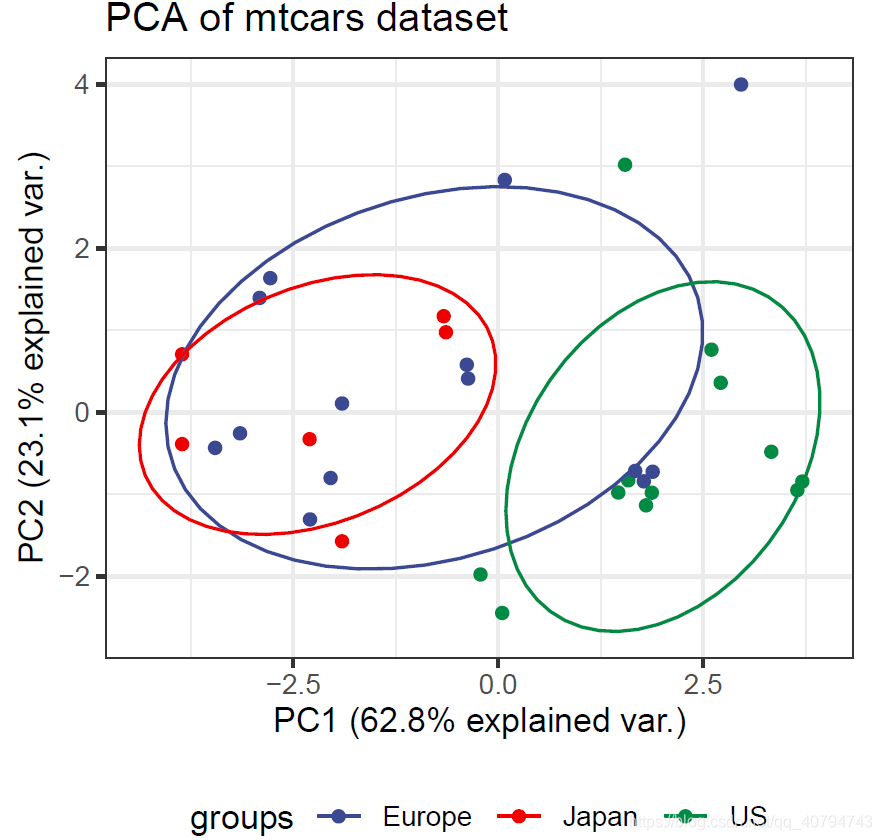
ggbiplot(da.fa.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,var.axes=FALSE, groups=data.country) +
  scale_colour_aaas()+
  ggtitle("PCA of mtcars dataset")+
  theme_bw()+
  theme(legend.position = "bottom")

在这里插入图片描述

4. ggscater可视化

library(ggpubr)
library(tidyverse)
da.fa.pca %>%  .$x %>% 
  as.data.frame() %>% 
  mutate(countary = c(rep("Japan", 3), rep("US",4), rep("Europe", 7),rep("US",3), 
                      "Europe", rep("Japan", 3), rep("US",4), rep("Europe", 3), "US", rep("Europe", 3))) %>%
  ggscatter(x = "PC1",y = "PC2",color = "countary",
            ellipse = T,size = 2,repel = T,
            main = "mtcars PCA plot") +
  theme_bw()

在这里插入图片描述
如果我们想得到样本之间的差异，则需要使用$rotation，一般情况下，生信中都是使用rotation来探究样本之间的差异。但是千万不要忽略我上面码的字哦，只有真正了解了PCA的原理以及结果数据，才能如鱼得水。

我这里没添加分组。

library(ggpubr)
library(tidyverse)
da.fa.pca %>%  .$rotation %>% 
  as.data.frame() %>% 
  ggscatter(x = "PC1",y = "PC2",
            size = 2,repel = T,
            main = "mtcars PCA plot") +
  theme_bw()

在这里插入图片描述

5. 番外：利用PCA score进行聚类分析

首先声明，PCA score是princomp()产生的结果。如果你想利用它，需要刚开始就使用它。这里仅作为演示。

hclust(dist(da.princomp$scores), method = "ward.D2") %>%
  plot()

在这里插入图片描述

#侵权联系删除！

参考

维基百科
R语言实战等书籍