「2019牛客多校第五场 I」three points 1【计算几何】

题意

• 就是给你一个大小为$w\times h$的矩形，然后让你在矩形内选三个点，使得三个点的距离分别为$a,b,c$

题解

• 考虑旋转或者翻转三角形使得其放得下为止，然后大概就是分类大讨论了
• 考虑枚举放在最下面的那条边【图中蓝色边】，可以将其正对$w$放下也可以正对$h$放下，这里值讨论正对$w$放下，另外一个类比即可
• 第一种情况，能放到$w$身上，$check$第三个点即可
  
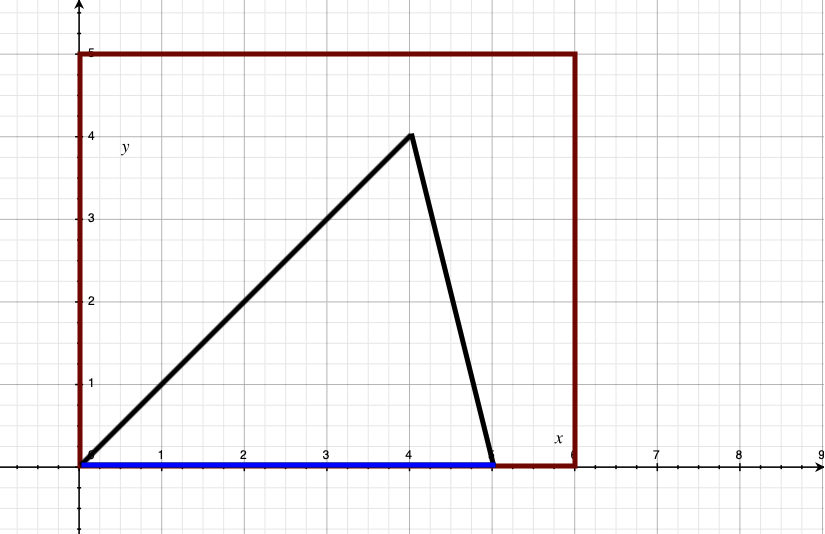
• 第二种情况，不能放下去，很容易算出上面那个点坐标
  
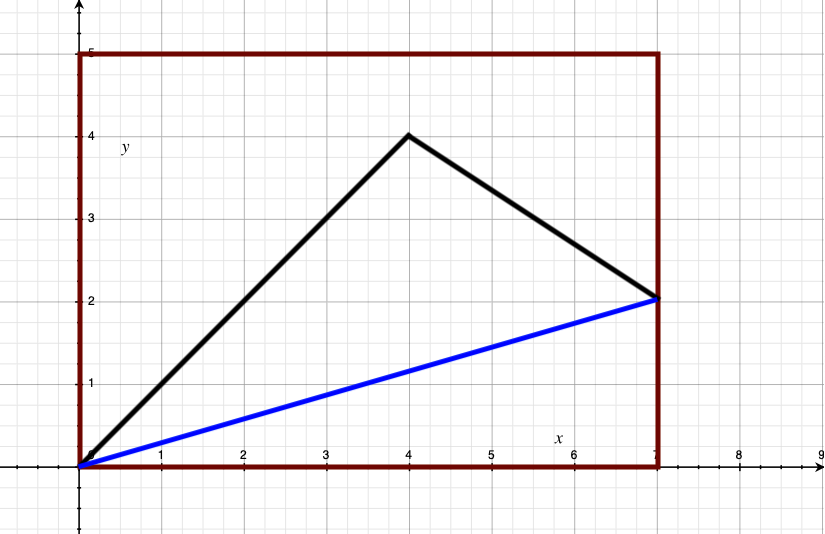
• 第三种情况容易忽视，即有可能需要倒着放
  
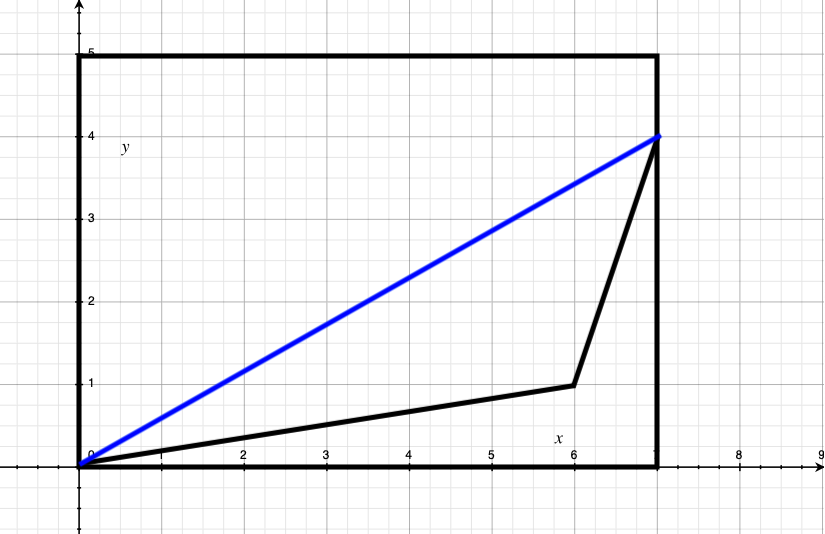
• 然后枚举每一条边作为底边和邻边，并且考虑正对$w$还是正对$h$放即可
• 又是一个多么痛的领悟，判断边界时需要写$<w+eps$和$h+eps$，赛场上只判了$>-eps$，上界没有加$eps$，天真的以为损失精度=数变小了，$wa$了一万年

代码

#include<bits/stdc++.h>

using namespace std;
const double eps=1e-8;
#define pi acos(-1.0)

int sgn(double k)
{
	return k<-eps?-1:(k<eps?0:1);
}

void print(double a) //数值a保留5位四舍五入输出,
{
	char buffer[1000];
	sprintf(buffer+1,"%.10lf",a);  //
	int len=strlen(buffer+1);
	bool ok=false;
	for(int i=1;i<=len;i++) if(!(buffer[i]=='.'||buffer[i]=='0'||buffer[i]=='-')) {ok=true;break;}
	if(ok) printf("%s",buffer+1);
	else printf("%.10lf",0.0);    //
}

typedef struct point{  //点结构体
	double x,y;
	point(double a=0,double b=0) {
		x=a;y=b;
	} 
	point operator+(point other) {
		return point(x+other.x,y+other.y);
	}
	point operator-(point other) {
		return point(x-other.x,y-other.y);
	}
	point operator*(double k) {
		return point(x*k,y*k);
	}
    friend double dis(point p1,point p2) {     //计算两点距离
        return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
    }

	friend point extend(point p,double len) { //将向量p长度变为len返回一个新的向量，方向不变
		if(sgn(dis(point(0,0),p))==0) return point(0,len);
		return point(p*(len/dis(point(0,0),p)));
	}

	friend point rotate(point p1,point p2,double a) {//点p2绕着点p1顺时针方向旋转a角度，a为弧度,返回新的point
		point vec=p2-p1;
		double xx=vec.x*cos(a)+vec.y*sin(a);
		double yy=vec.y*cos(a)-vec.x*sin(a);
		return point(p1.x+xx,p1.y+yy);
	}
}Vector;

bool valid(point p1,double w,double h) 
{
	return sgn(p1.x)>=0&&sgn(p1.x-w)<=0&&sgn(p1.y)>=0&&sgn(p1.y-h)<=0;
}

point ans[3];
bool check(double w,double h,double x,double y,double z,int a,int b,int c)
{
	if(sgn(sqrt(w*w+h*h)-x)<0) return false;
	double angle_y=acos((x*x+z*z-y*y)/(2*x*z));
	if(sgn(x-w)<=0) {	
		
		Vector cur=extend(Vector(x,0),z);
		ans[a]=point(x,0);ans[c]=point(0,0);ans[b]=cur;

		point res=rotate(ans[c],ans[b],2*pi-angle_y);
		if(valid(res,w,h)) {ans[b]=res;return true;} 
	}else{
		double he=sqrt(x*x-w*w);
		Vector cur=extend(Vector(w,he),z);
		ans[a]=point(w,he);ans[c]=point(0,0);ans[b]=cur;
		
		point res=rotate(ans[c],ans[b],angle_y);
		if(valid(res,w,h)) {ans[b]=res;return true;} 
		res=rotate(ans[c],ans[b],2*pi-angle_y);
		if(valid(res,w,h)) {ans[b]=res;return true;} 
	}

	if(sgn(x-h)<=0) {
		Vector cur=extend(Vector(0,x),z);
		ans[a]=point(0,x);ans[c]=point(0,0);ans[b]=cur;

		point res=rotate(ans[c],ans[b],angle_y);
		if(valid(res,w,h)) {ans[b]=res;return true;} 
	}else {
		double he=sqrt(x*x-h*h);
		Vector cur=extend(Vector(he,h),z);
		ans[a]=point(he,h);ans[c]=point(0,0);ans[b]=cur;
		
		point res=rotate(ans[c],ans[b],angle_y);
		if(valid(res,w,h)) {ans[b]=res;return true;}
		res=rotate(ans[c],ans[b],2*pi-angle_y);
		if(valid(res,w,h)) {ans[b]=res;return true;}		
	}
	return false;
}

void outt()
{
	for(int i=0;i<=2;i++) {
		print(ans[i].x);printf(" ");
		print(ans[i].y);printf(i==2?"\n":" ");
	}
}

int main()
{
	int t;scanf("%d",&t);
	while(t--) {
		double w,h,a,b,c;scanf("%lf %lf %lf %lf %lf",&w,&h,&a,&b,&c);
		if(check(w,h,a,b,c,0,2,1)) {outt();continue;}
		if(check(w,h,a,c,b,1,2,0)) {outt();continue;}
		if(check(w,h,b,a,c,0,1,2)) {outt();continue;}
		if(check(w,h,b,c,a,2,1,0)) {outt();continue;}
		if(check(w,h,c,a,b,1,0,2)) {outt();continue;}
		if(check(w,h,c,b,a,2,0,1)) {outt();continue;}
		assert(false);
	}
}