目录
3.List(arraylist,linkedlist,array)
3.2.2 ArrayList list = new ArrayList(10)中list 扩容了几次
4.3.9 HashMap、HashTable和ConcurrentHashMap?
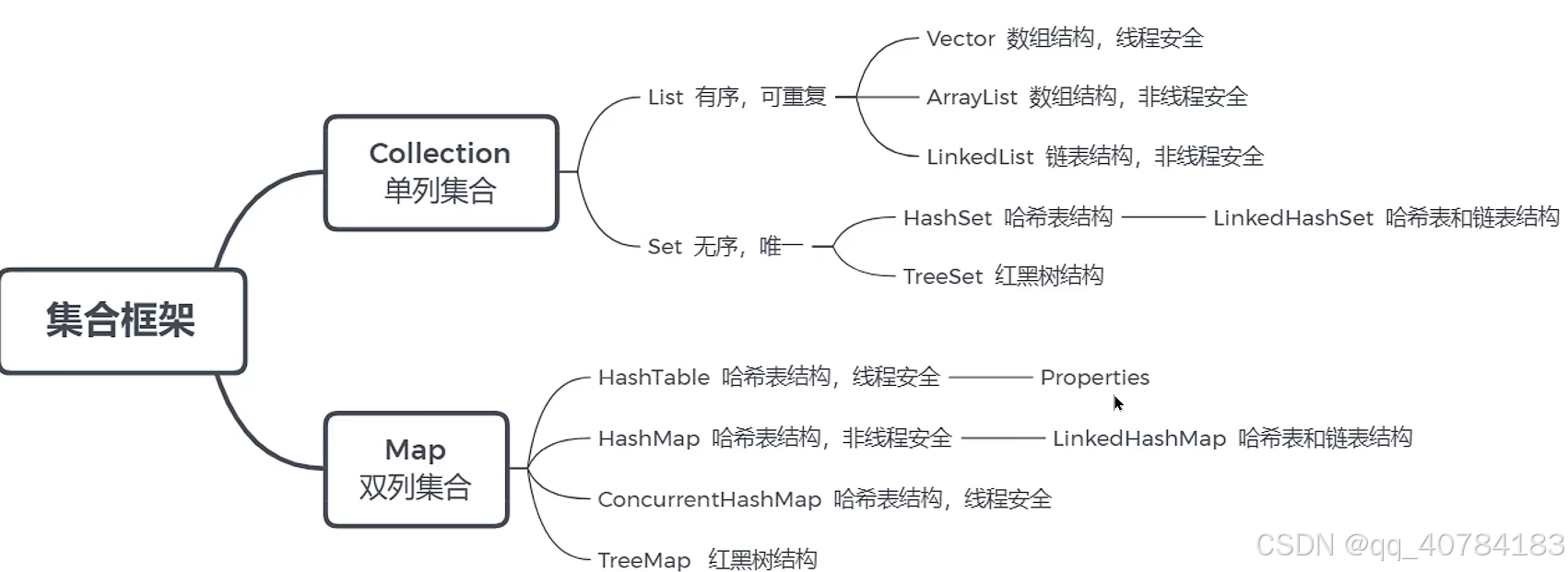
1.集合框架
2. 算法复杂度分析
2.1 时间复杂度

2.2 空间复杂度

3.List(arraylist,linkedlist,array)
3.1 数组
- 数组是一种用连续的内存空间存储相同的数据类型数据的线性数据结构。
- 索引从0开始,步长为1.
- 其中未知下标,查询就得自己for循环遍历查询了
3.1.1 数组下标为啥从0开始?
- 历史原因,早期的编程语言如C语言在设计时就采用了从0开始计算
减少cpu指令 arr[i] = base_address + i * type_size(从1开始这里i还要减1)
物理内存的地址是从0开始的
3.1.2 时间复杂度?
随机查找,时间复杂度O(1)
未知下标查找O(n)
删除和插入的时候需要移动数组 O(n)
3.1.3 数组初始化?
1.静态初始化:
语法:
数组元素类型[] 数组名 = new 数组元素类型[]{元素1,元素2,元素3,…};
举例:
int[] nums = new int[]{1,3,5,7,9};
简单写法,必须声明之后,立刻初始化,不能先声明后初始化:
int[] nums = {1,3,5,7,9};
2.动态初始化:
由我们来设置数组的元素个数(数组长度),而每一个数组元素的初始值有系统决定.
语法:
数组元素类型[] 数组名 = new 数组元素类型[ length ];
比如:
int[] ages = new int[100];
3.注意:静态初始化和动态初始化不能同时使用 int[] nums = new int[5]{1,3,5,7,9};错误写法
3.2 arraylist 源码分析
3.2.1 底层实现原理
ArrayList底层是用动态的数组实现的。
ArrayList初始容量为0,当第一次添加数据的时候才会初始化容量为10.
ArrayList在进行扩容发的时候变为原来的1.5倍,每次扩容都需要拷贝数组。
ArrayList在添加数据的时候
确保数组伊使用长度(size)加1之后足够存下下一个数据。
计算数组容量,如果当前数组已使用长度+1后大于当前数组长度,则调用grow方法扩容(1.5倍)。
确保新的数据有地方存储后,则将新元素添加到位于size的位置山上。
返回添加成功布尔值。
3.2.2 ArrayList list = new ArrayList(10)中list 扩容了几次
- 该语句看源码的只传参数并不会扩容,直接实例化一个10的
- 这种是指定数组大小的创建,创建时直接分配其大小,没有扩充。
3.2 .3 数组和list之间的转换?
数组转List,使用jdk的java.util.array工具类asList方法
List转数组,使用List的ToArray方法.
3.2.4 上面说的,转换完后,修改源数据,影响吗?
- 1. 数组转集合会,没有新建list,直接引用传递的
- 2. 不会 toarray方法中复制数据到新对象了
3.2.5 遍历时移除元素 ?
- 直接for循环可以倒序
- 可以使用迭代器
Iterator itr = list.iterator();
while(itr.hasNext()) {
if(itr.next().equals("ss") {
itr.remove();
}
}
3.3 LinkedList
3.3.1 单项链表和双向链表的区别是?
- 单向链表只有一个方向,节点只有一个后继指针next
- 双向有两个方向,每个节点不知有后继指针,还有前驱指针
单向链表优缺点:
1、优点:单向链表增加删除节点简单。遍历时候不会死循环;
2、缺点:只能从头到尾遍历。只能找到后继,无法找到前驱,也就是只能前进。
双向链表优缺点:
1、优点:可以找到前驱和后继,可进可退;
2、缺点:增加删除节点复杂,多需要分配一个指针存储空间。
3.3.2 arraylist和Llinedlist 区别


4. map相关
4.1 二叉搜索树
4.1.1 二叉树
- 是一种特殊的树状结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
- 二叉树的定义可以递归地描述为:一个二叉树要么是一棵空树,要么是一棵由一个根节点和两棵互不相交的二叉树组成的非空树
4.1.2 二叉搜索树
搜索树的话,特殊情况下会成为一根线,o(n),所以不会用
是一种特殊的二叉树,它满足以下性质:
- 节点值排序:每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
- 递归性质:左子树和右子树也必须符合这个规则。
- 快速查找:由于二叉搜索树的这一特性,使得查找效率非常高,类似于二分查找1
4.2 红黑树
4.2.1 概念
- 红黑树(Red Black Tree) 也是一种自平衡的二叉搜索树(BST)
- 所有的红黑规则都是希望红黑树能够保证平衡
- 红黑树的时间复杂度:查找,添加删除 都是 O(logn)
4.2.2 红黑树实现?
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 每个叶节点(NIL节点,空节点)是黑色。
- 如果一个红色节点有子节点,那么子节点的颜色是黑色。
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
4.3 散列表
4.3.1 什么是?
- 散列表(Hash Table)又名哈希表/Hash表
- 根据键(Key)直接访问在内存存储位置值(Value)的数据结构
- 由数组演化而来,利用了数组支持按照下标进行随机访问数据
4.3.2 散列冲突?
- 散列冲突指的是当两个不同的键经过哈希函数计算后得到相同的哈希值,导致它们应该存储在哈希表中的相同位置。
- 由于哈希表的存储位置是通过哈希函数计算得到的,因此在实际应用中,可能会出现多个键映射到同一个位置的情况,这就是散列冲突。
4.3.3 解决?
开放寻址法(Open Addressing):在发生冲突时,通过一定的探测序列(如线性探测、二次探测、双重散列等)在哈希表中寻找下一个可用的位置来存储冲突的键值对。
链地址法(Chaining):在哈希表的每个槽位(桶)中维护一个链表(或其他数据结构),将哈希值相同的键值对存储在同一个位置的链表中。
再哈希(Rehashing):当哈希表中的填充因子达到一定阈值时,可以进行再哈希操作,即重新调整哈希表的大小并重新计算所有键的哈希值,以减少冲突的概率。
建立二级哈希表:在发生冲突时,可以使用第二个哈希函数计算一个新的位置,以解决冲突。
线性探测再散列(Linear Probing Rehashing):结合了开放寻址法和再哈希的思想,当发生冲突时,通过线性探测找到下一个可用位置,并在需要时重新调整哈希表的大小。
4.3.4 HashMap实现原理

4.3.5 put方法

4.3.6 hashMap扩容

4.3.7 hashMap寻址算法()

4.3.8 1.7hashmap死循环怎么办?

4.3.9 HashMap、HashTable和ConcurrentHashMap?
| 特性 | HashMap | HashTable | ConcurrentHashMap |
|---|---|---|---|
| 线程安全 | 非线程安全 | 线程安全 | 线程安全 |
| 性能 | 高 | 低 | 高 |
| 允许null键值 | 是 | 否 | 是 |
| 迭代器快速失败 | 是 | 否 | 是 |
| 锁机制 | 无 | 同步方法 | 分段锁(Segment) |
| 遗留类 | 否 | 是 | 否 |
综上所述,HashMap适合在单线程环境下使用,性能较高;HashTable适合在多线程环境下使用,但性能较低,不推荐使用;ConcurrentHashMap是在多线程环境下性能较好的选择,支持高并发访问。在实际开发中,根据需求选择合适的实现类来保证数据的安全性和性能。
4.3.10 HashSet是如何保证不重复的?
基于HashMap的唯一性:在HashSet内部实际上是使用一个HashMap来存储元素的,其中HashMap的key存储元素,而value则存储一个固定的Object对象。由于HashMap的key是唯一的,这就保证了HashSet中不会有重复元素。
利用hashCode和equals方法:当元素被添加到HashSet时,HashSet会首先调用该元素的hashCode方法得到其哈希值,然后根据哈希值确定该元素在内部HashMap中的存储位置。如果两个元素的hashCode相同,HashSet会继续调用它们的equals方法进行比较,以确保元素的唯一性。
不允许重复元素:由于HashMap的key是唯一的,当尝试向HashSet中添加一个已经存在的元素时,新元素的hashCode和equals方法会与已有元素进行比较,如果相同则新元素不会被添加,从而保证了HashSet中不会有重复元素。

























 699
699

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










