B_Tree插入删除算法分析

B_Tree简单介绍

B_Tree是一种基础而又复杂树形结构。它是一棵多叉树，它的叶子节点都在同一深度，无需向AVLTree一样进行手动的平衡。B_Tree还衍生出了后继的B+_Tree等结构。（在我看来B_Tree与红黑树，跳跃表等有很多相似之处）

B_Tree(2-3-4阶B_Tree)的主要操作

插入数据操作

插入数据操作步骤：

1. 找到对应的插入节点，进行数据插入
2. 插入数据后对该节点进行检测，判断当前节点所拥有的数据总数，是否超出当前节点所能容纳的数据总数。

• 若没有超过，则插入结束
• 否则需要进行节点分裂

3.若当前节点进行了，分裂意味着父节点多了一个儿子节点。故父节点也需要判断是否需要进行分裂。因此，该插入函数需要递归进行。

算法简述：

寻找插入数据的节点并插入数据，比较简单，这里不详述。
对于分裂节点，比较关键。我的做法：

• 创建一个新节点
• 将源节点**一半（或一半-1）**的数据分给新节点（我这里默认将后半部分分给新节点）
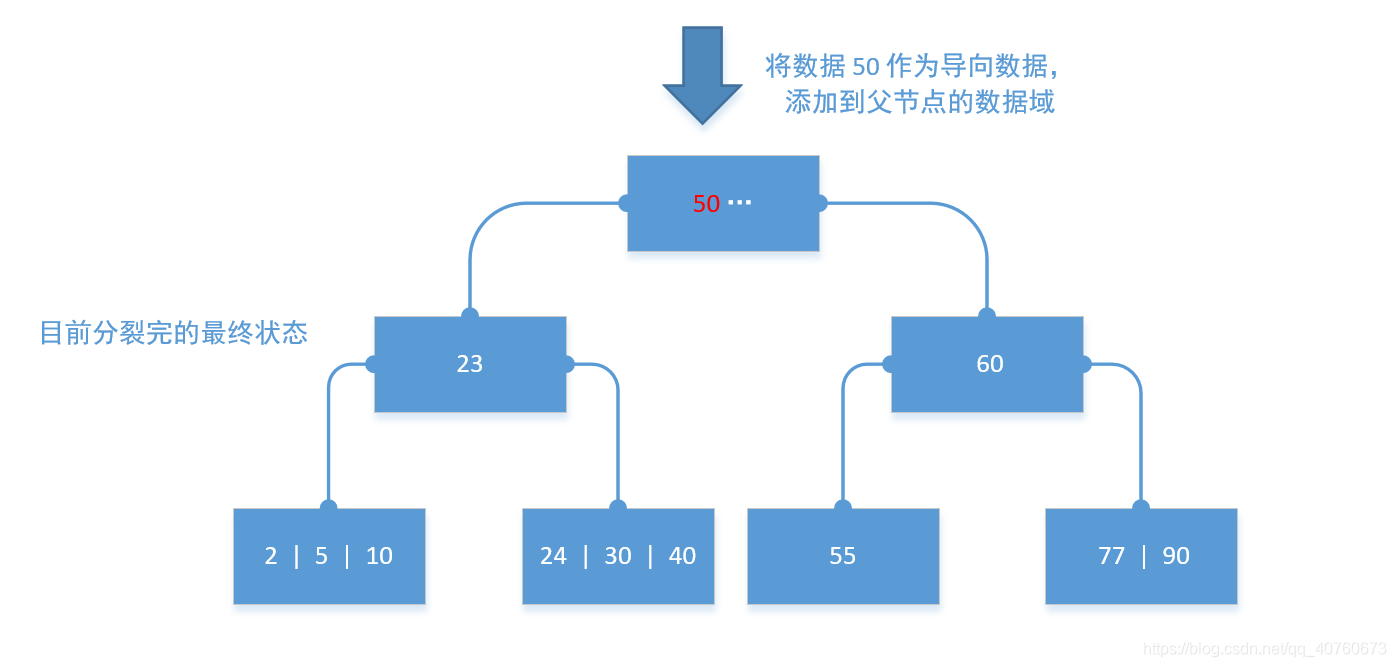
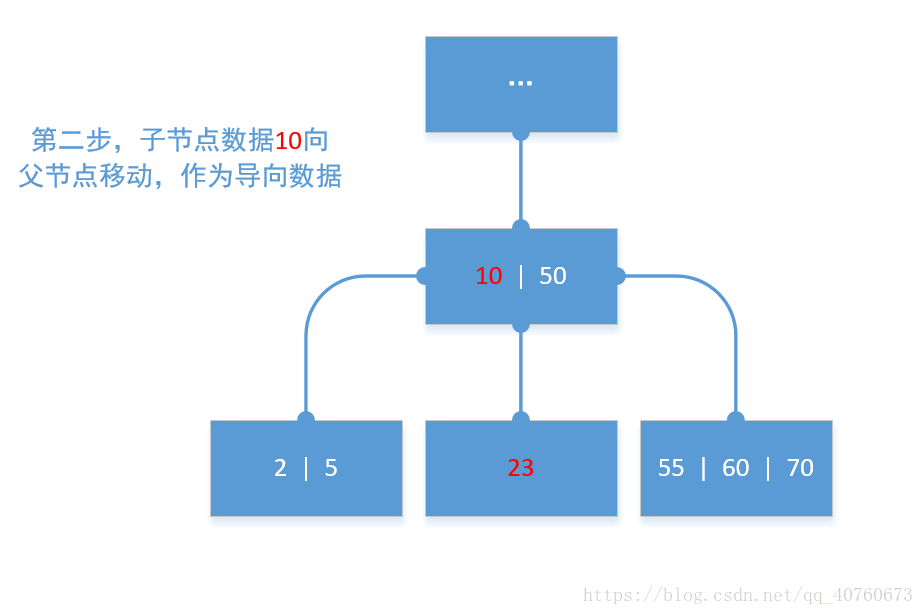
• 从源节点中提取最后一个数据添加到父节点（作为一个 导向数据）。以下的图可以较好的描述这个分裂过程。

由于插入数据函数需要判断父节点是否也需要分裂，故我实现的时候使用的递归。（有非递归的实现方法当然更好！）

以下分裂模拟：

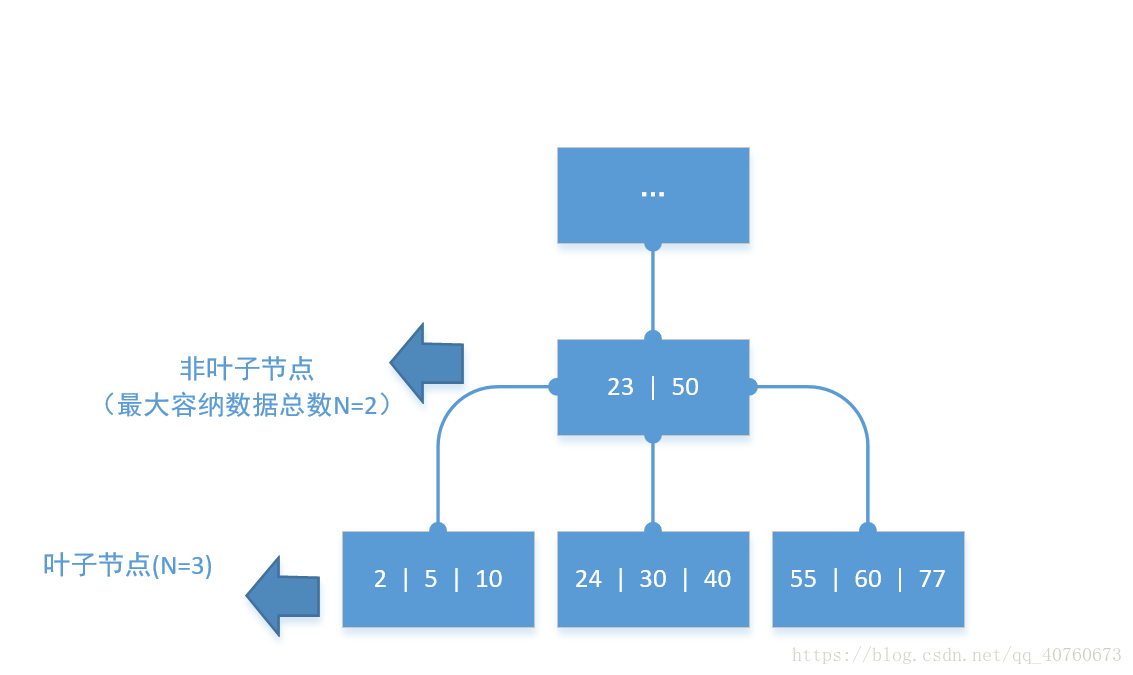
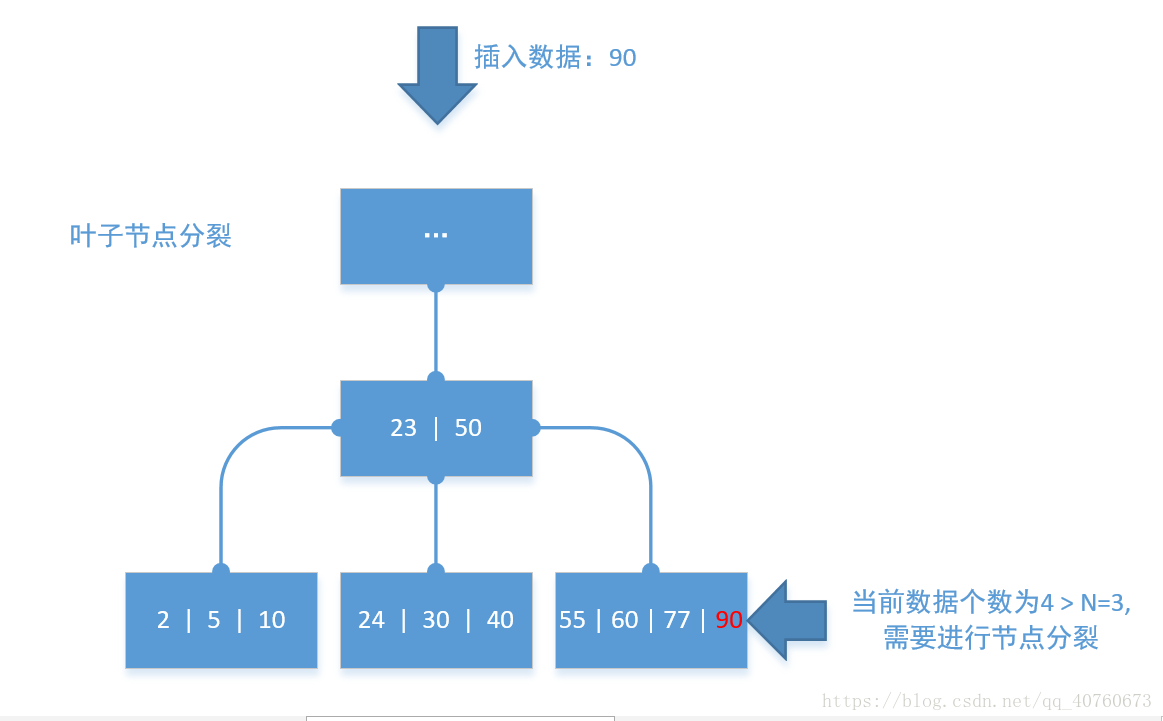
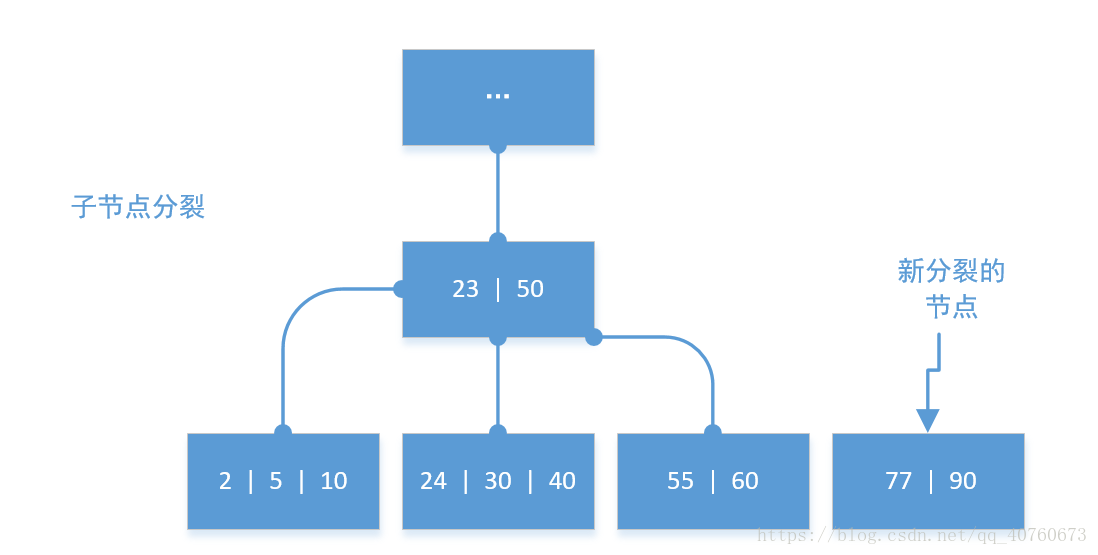
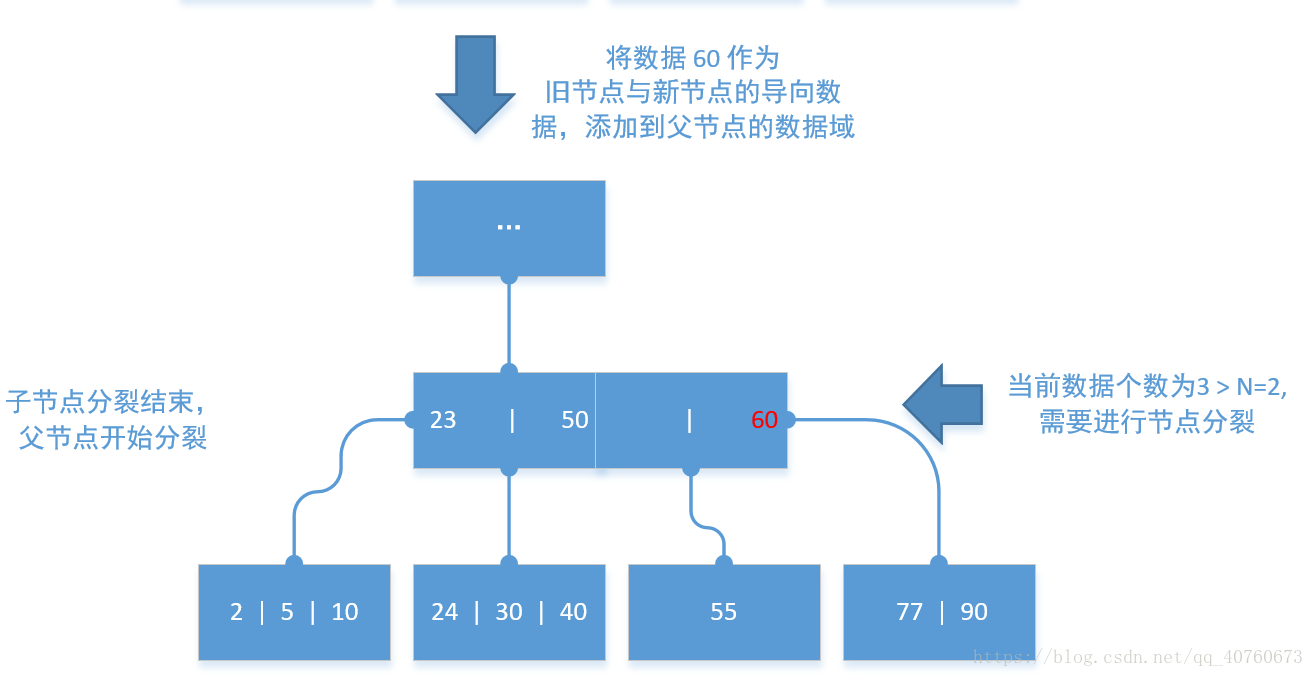
删除数据操作

删除数据操作步骤

1. 找到删除数据的节点
2. 判断删除的数据是否在叶子节点上

• 若删除的节点在叶子上，则直接进行数据删除。
• 否则需要找到该删除数据的代替数据。将代替数据代替掉删除数据后，执行删除代替数据。

3. 删除掉数据后，可能会造成当前节点的数据过少，这时有两种操作。
   1. 合并节点操作：
      合并操作是将兄弟节点与当前节点进行合并。条件：当当前节点与兄弟节点的数据总和不超过当前节点所能容纳的总数+1时.（+1是因为这父节点相对于两个节点的导向数据也需要进行合并，详情看后面的模拟图）
   2. 数据移动操作：
      当合并不允许的时候，则从兄弟节点要一部分数据到当前节点。（详情看后面的模拟图）
4. 判断合并节点后是否会导致父节点的子结点总数过少，若过少需要进行第3步操作。（由于涉及到了父节点，故我的实现使用了递归）

算法简述：

1. 合并节点算法：
   • 先判断当前节点数据总数 + 兄弟节点的数据总数 + 1 <= 当前节点所能容纳的总数是否成立。成立即可进行合并。
   • 将 兄弟节点和当前节点的数据和导向数据及其子节点的指针域进行合并成为一个节点

以下合并模拟图：

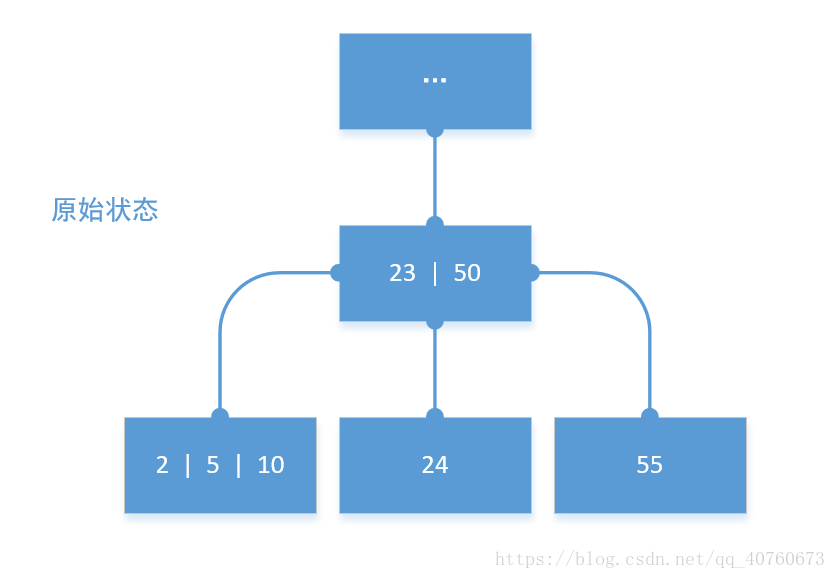
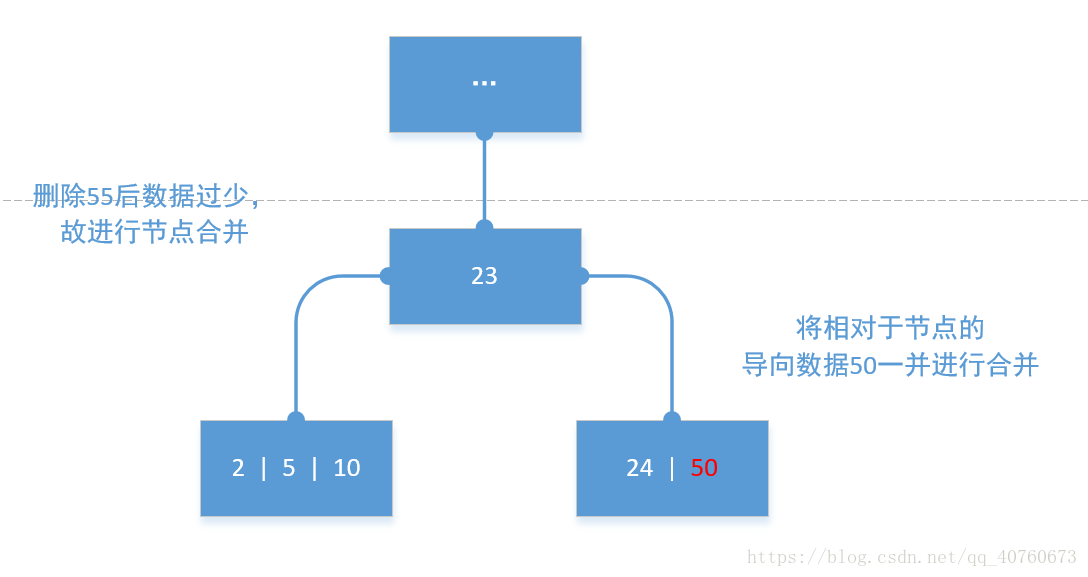
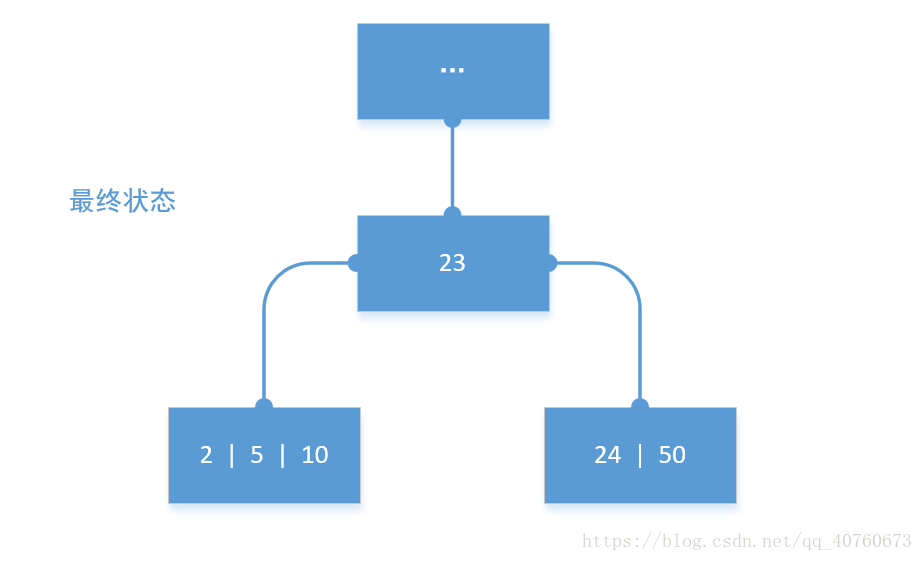
2. 移动数据：
   • 当合并节点条件不满足时。我们则可以进行数据移动操作（原因：无法合并说明有一兄弟节点有大量的数据）。
   • 若 左兄弟或右兄弟 兄弟节点数据总数 > 可容纳数据总数 / 2，则从该兄弟节点要一部分数据及其子节点到当前节点。
   • 进行移动数据（包括子节点的移动）。（移动过程具体看以下模拟图）

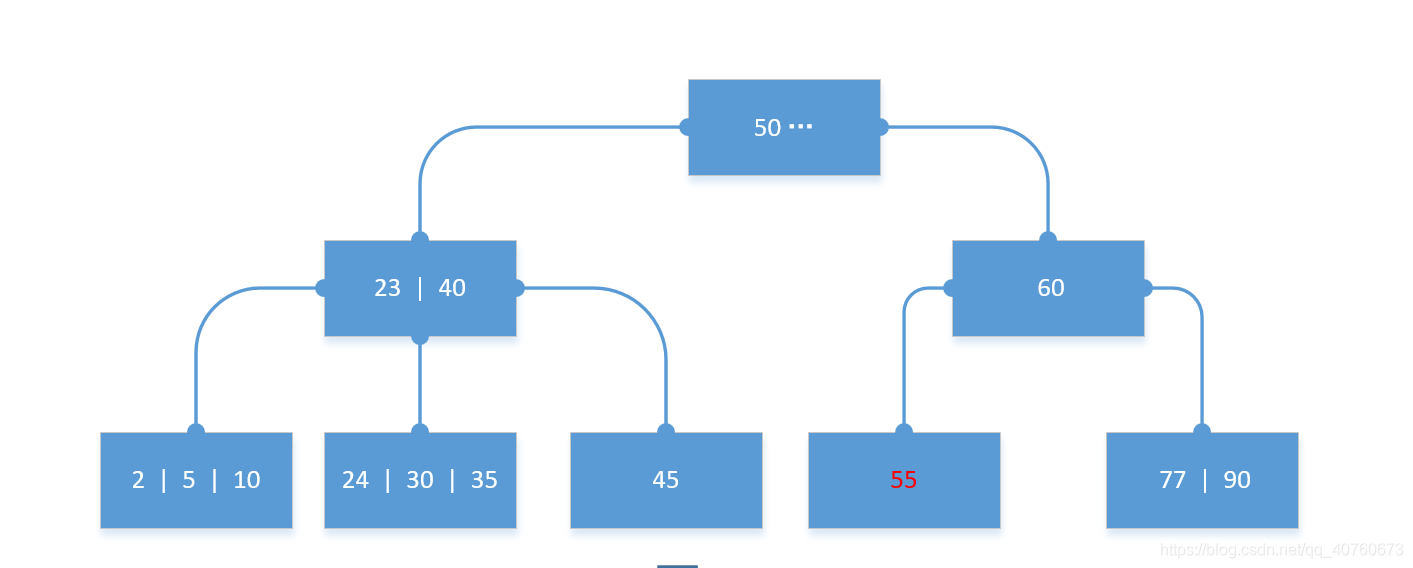
移动数据模拟图：

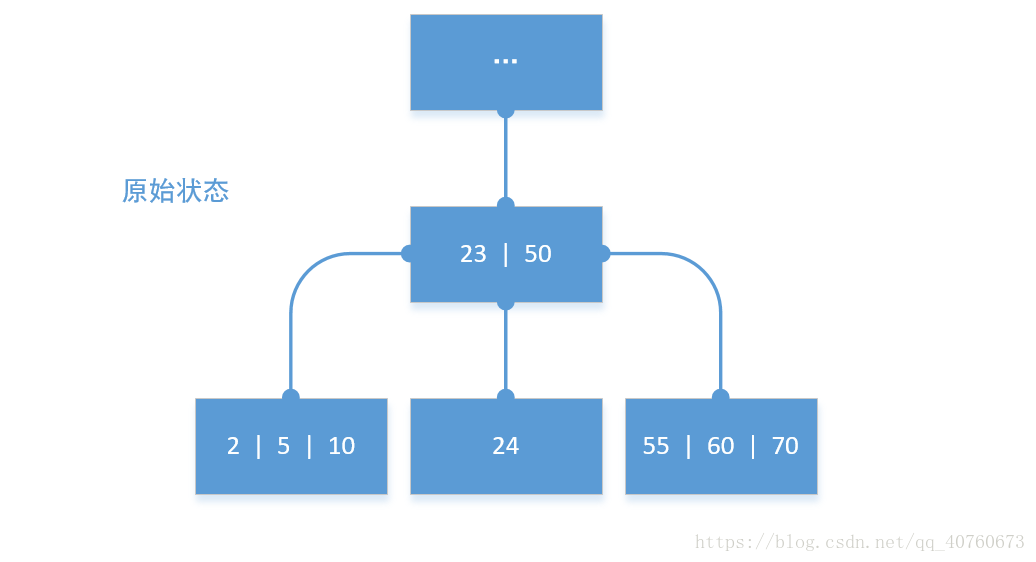
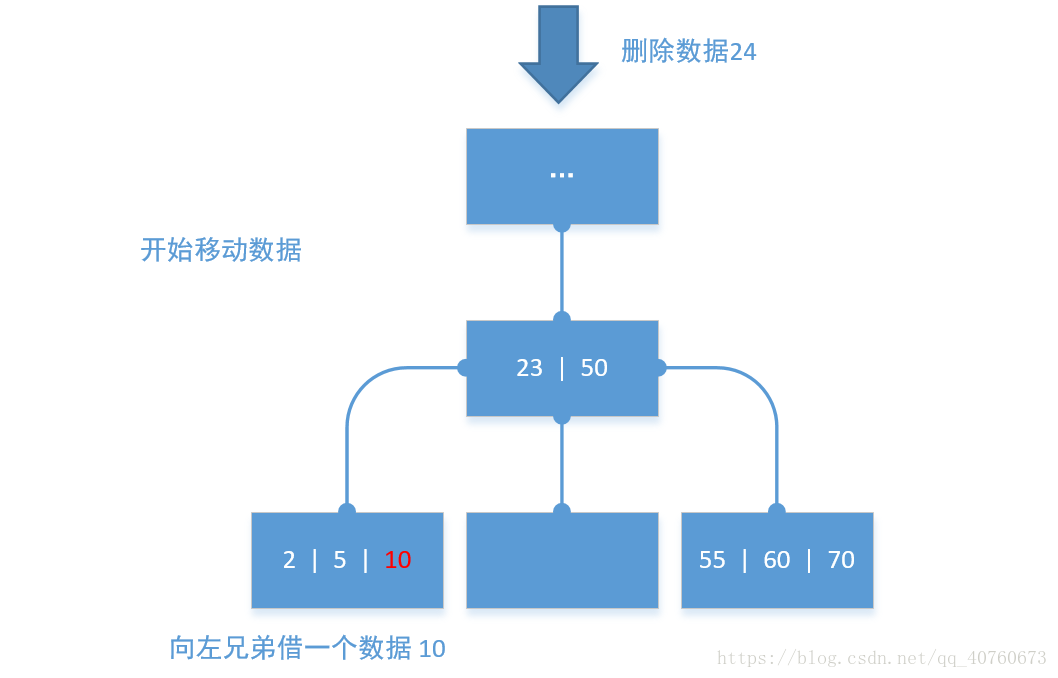
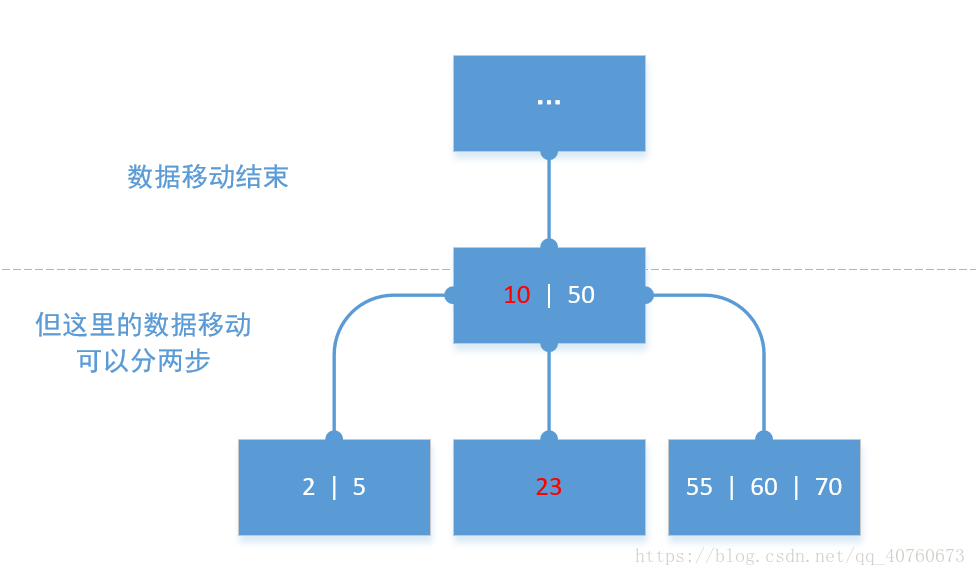
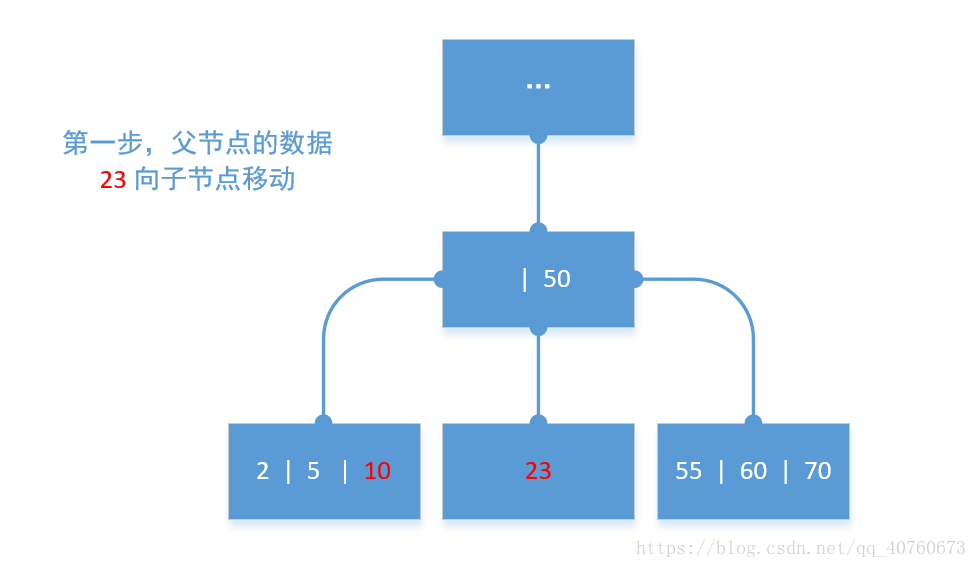
包括子节点的数据移动操作的模拟图：



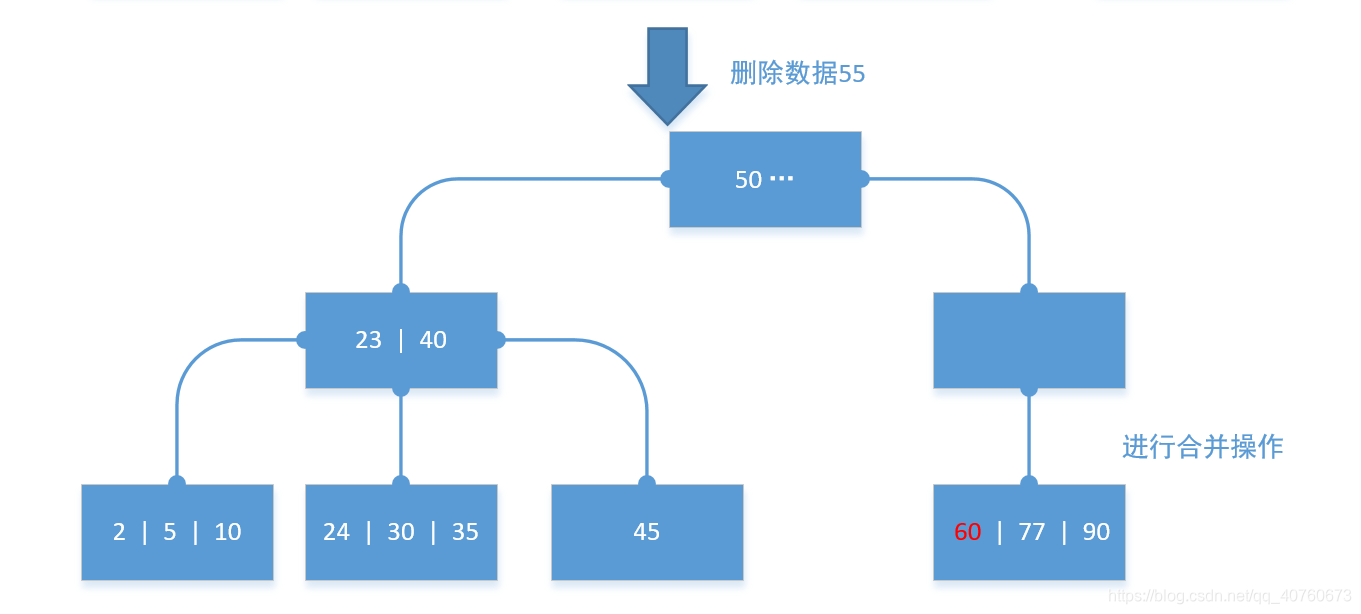
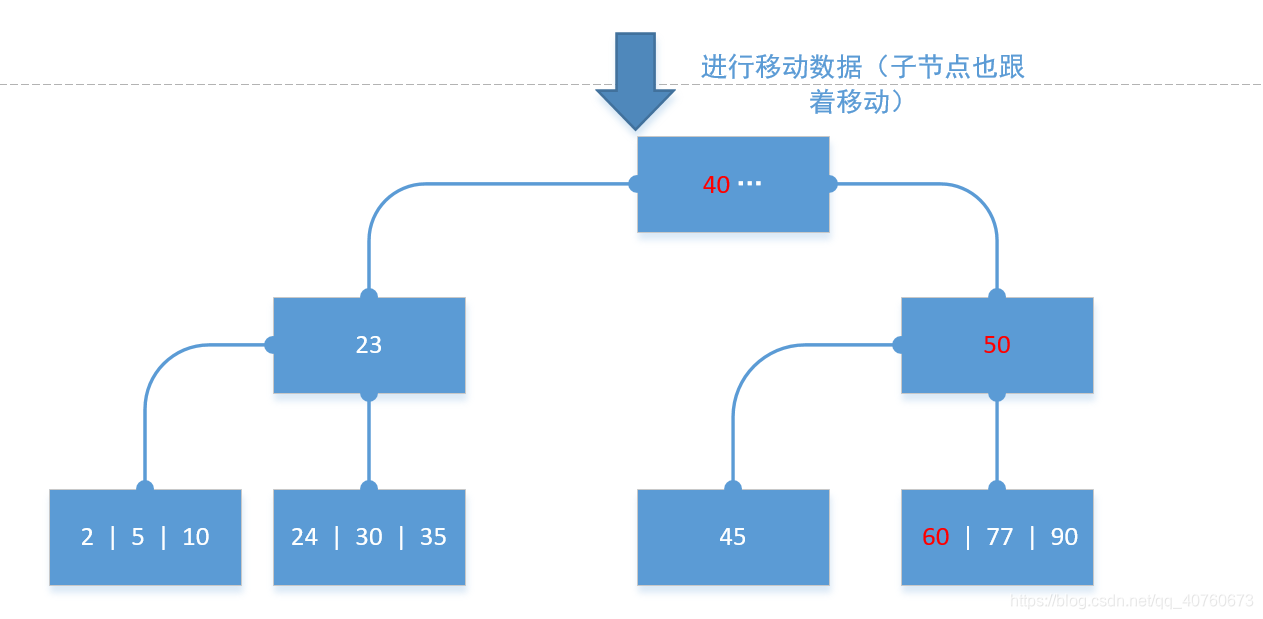
模拟结束。

B_Tree的插入与删除分析到此为止。欢迎指出错误，或提出建议。