冒泡排序从前向后/从后向前实现

一、什么是冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

二、动图演示

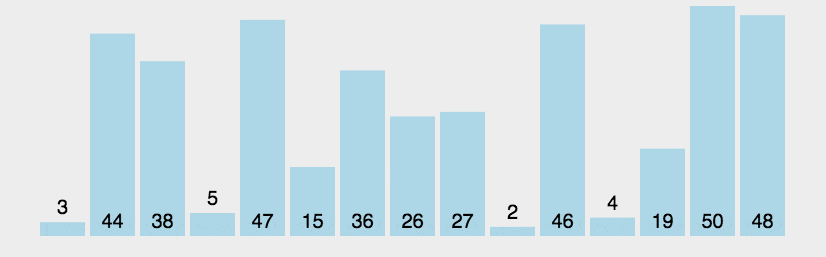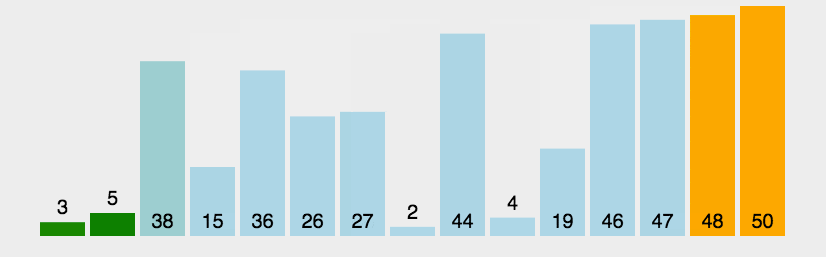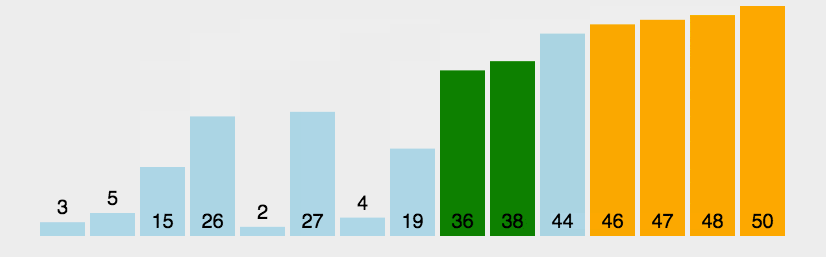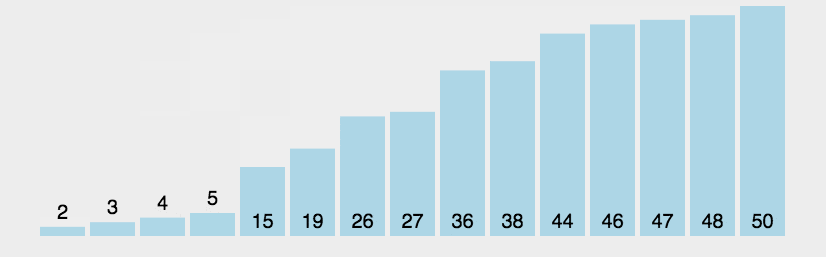
*动图来自菜鸟教程

三、实现方式

比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

四、关于冒泡排序的性能参数

1、时间复杂度

最好：$O(n)$（有序
平均：$O(n^2)$
最差：$O(n^2)$

2、空间复杂度

$O(1)$

3、是否稳定

稳定-比较和交换过程，判断到相同的元素时候，不会进行交换的

4、适用于何类型存储

顺序存储和链式存储

五、代码实现

c++:

1、j=n-1从后向前

*此处使用到了flag

冒泡排序还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。

void BubbleSort(ElemType A[],int n ){
    for(int i = 0; i<n-1; i++){		// n-1次冒泡
        bool flag = false;
        for(int j = n - 1; j>i; j--)	// 从后向前
            if(A[j-1] > A[j]){	//逆序
                swap(A[j-1],A[j]);
                flag = true;		// 只有交换了flag才为true
            }
        if(flag == false)		//冒泡完成
            return;
    }
}

2、j=0 从前向后

还是这种好记，上一种要变的量有点多

void BubbleSort(ElemType A[],int n ){
    for(int i = 0; i<n-1; i++){		// n-1次冒泡
        for(int j = 0; j< n-1-i; j++)	// 从前向后
            if(A[j] > A[j+1]){	//逆序
                swap(A[j],A[j+1]);
            }
    }
}

实例实现：

/*
 * @Descripttion: 
 * @version: 
 * @Author: edisonhuang
 * @Date: 2020-03-09 16:20:29
 * @LastEditors: edisonhuang
 * @LastEditTime: 2020-03-09 16:31:07
 */
#include <iostream>
void BubbleSort1(int A[], int n);
void BubbleSort2(int A[], int n);
void Print(int A[],int n);
using namespace std;

int main()
{
    int arr1[] = {13, 14, 8, 100, 25, 75, 9, 64, 12};
    int len1 = (int) sizeof(arr1) / sizeof(*arr1);
    Print(arr1,len1);
    BubbleSort1(arr1,len1);
    Print(arr1,len1);

    int arr2[] = {13, 14, 8, 100, 25, 75, 9, 64, 12};
    int len2 = (int) sizeof(arr1) / sizeof(*arr1);
    Print(arr2,len2);
    BubbleSort2(arr2,len2);
    Print(arr2,len2);

    return 0;
}

void BubbleSort1(int A[], int n){
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n-1-i; j++)
        {
            if (A[j] > A[j+1])
            {
                swap(A[j],A[j+1]);
            }   
        }
    }
}
void BubbleSort2(int A[], int n){
    for (int i = 0; i <  n - 1 ; i++)
    {
        for (int j = n - 1; j > i; j--)
        {
            if (A[j-1] > A[j])
            {
                swap(A[j-1], A[j]);
            }
        }
    }
    
    
}
void Print(int A[],int n ){
    for (int i = 0; i < n; i++)
    {
        cout << A[i] << " ";
    }
    cout << endl;
}