【数字图像处理】第4章 图像的几何变换

4 图像的几何变换

---

图像的几何变换
图像的几何变换包括了图像的形状变换和图像的位置变换。
图像的形状变换是指图像的放大、缩小与错切。
图像的位置变换是指图像的平移、镜像与旋转。
图像的仿射变换是采用通用的数学影射变换公式，来表示几何变换。
图像的几何变换不改变像素的值，只改变像素的位置。

（一）图像的位置变换

所谓图像的位置变换是指图像的大小和形状不发生变化，只是将图像进行平移、镜像和旋转。
图像的位置变换主要是用于目标识别中的目标配准。

1）图像的平移

2）图像的镜像

3）图像的旋转

图像的旋转计算公式如下：
$x_1=x_{0}cos(a)-y_{0}sin(a);$
$y_1=x_{0}sin(a)+y_{0}cos(a);$

• 这个计算公式计算出的值为小数，而坐标值为正整数。
• 这个计算公式计算的结果值所在范围与原来的值所在的范围不同。
• 因此需要前期处理：扩大画布，取整处理，平移处理 。

---

图像旋转之前，为了避免信息的丢失，画布的扩大是最重要的。

画布扩大的原则是：以最小的面积承载全部的画面信息。

---

图像旋转后处理

• 旋转后的隐含问题分析
  图像旋转之后，出现了两个问题：
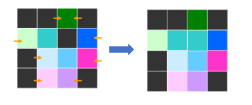
  1）像素的排列不是完全按照原有的相邻关系。这是因为相邻像素之间只能有8个方向（相邻为45度），如下图所示。
  2）会出现许多的空洞点。
  
• 解决问题的思路
  出现问题的核心是像素之间的连接是不连续的。
  相邻像素的角度是无法改变的，所以只能通过增加分辨率的方法来从整体上解决这个问题。
  采用某种填补方法来填充空洞。
• 插值
  最简单的方法是行插值（列插值）方法。
  1）找出当前行的最小和最大的非背景点的坐标，记作：$(i,k_1)$、$(i,k_2)$。如下图有：
  (1,3)、(1,3); (2,1)、(2,4);
  (3,2)、(3,4)； (4,2)、(4,3)。
  2）在$(k_1,k_2)$范围内进行插值，插值的方法是：
  空点的像素值等于前一点的像素值。
  3）同样的操作重复到所有行。
  • 经过插值处理之后，图像效果就变得自然。
  

---

图像的旋转——反变换
反变换方法就是从新图形的像素坐标反过来计算对应原图像坐标点的坐标。旋转角度$a\to -a$
即将图像的旋转计算公式改写：
$x_1=x_{0}cos(a)-y_{0}sin(a);$
$y_1=x_{0}sin(a)+y_{0}cos(a);$
改写为
$x_0=x_{1}cos(a)+y_{1}sin(a);$
$y_0=-x_{1}sin(a)+y_{1}cos(a);$

（二）图像的形状变换

图像的形状变换主要是指图像的缩小、放大与错切。 通常在目标物识别中使用

1）图像缩小

分为按 比例缩小 和 不按比例缩小 两种。
图像缩小之后，因为承载的信息量小了，所以画布可相应缩小.

方法1：基于像素采样的图像缩小方法
图像缩小实际上就是对原有的多个数据进行挑选或处理，获得期望缩小尺寸的数据，并且尽量保持原有的特征不丢失。
最简单的方法就是等间隔地选取数据。

实现方法
设原图像大小为$M\ast N$，缩小为$k_{1}M\ast k_{2}N$，（$k_1<1$，$k_2<1$）。算法步骤如下：
1）设原图为$F(x,y)，x=1,2,\dots ,M,y=1,2,\dots ,N.$ 压缩后图像是$G(i,j),i=1,2,\dots ,k_{1}M,j=1,2,\dots ,k_{2}N.$
2）$G(i,j)=F(c_1\ast i,c_2\ast j)$ 其中，$c_1=\frac{1}{k_1},c_2=\frac{1}{k_2}$

方法2：基于局部均值的图像缩小方法

2）图像放大

图像放大从字面上看，是图像缩小的逆操作，但从信息处理的角度来看，则难易程度完全不一样。
图像缩小是从多个信息中选出所需要的信息，而图像放大则是需要对多出的空位填入适当的值，是信息的估计。

方法1：基于像素填充的图像放大方法

实现方法
设原图像大小为$M\ast N$，放大为$k_{1}M\ast k_{2}N$，（$k_1>1$，$k_2>1$）。算法步骤如下：
1）设旧图像是$F(x,y)，x=1,2,\dots ,M,y=1,2,\dots ,N.$ 新图像$G(i,j),i=1,2,\dots ,k_{1}M,j=1,2,\dots ,k_{2}N.$
2）$G(i,j)=F(c_1\ast i,c_2\ast j)$ 其中，$c_1=\frac{1}{k_1},c_2=\frac{1}{k_2}$

方法2：基于双线性插值的图像放大方法

（三）图像的仿射变换

图像仿射变换提出的意义是采用通用的数学影射变换公式，来表示前面给出的几何变换。
为了适应平移,提出了齐次坐标的概念。

齐次坐标
原坐标为 $(x,y)$，定义齐次坐标为：$（wx,wy,w）$
实质是通过增加一个坐标量来解决问题。

通式

图像几何变换的表示

bingo~   ✨ 只要还活着，就不会有坏结局，我们仍然在故事的中途