基于堆栈的背包问题

问题描述：假设有一个能装入总体积为T的背包和n件体积分别为w_1,w_2,...w_n的物品,能否从n件物品中挑选若干件恰好装满背包，即使w_1+w_2+...+w_n=T，要找出所有满足上述条件的解。

测试数据：T=10，各件物品的体积为{1，8，4，3，5，2}，可找到下列4组解：

（1，4，3，2）、（1，4，5）、（8，2）、（3，5，2）

基本要求：

（1）、设计一个背包问题的函数。

（2）、编写一个测试主函数。

测试数据：T=10,各件物品的体积为{1，8，4，3，5，2}。

算法思想：

        首先将物品排成一列，然后顺序选取物品装入背包中。假设选取了前i件物品之后还没有装满，则继续选取第i+1件物品；若该件物品“太大”不能装入，则弃之而继续选取下一件，直至背包装满为止；但如果在剩余的物品中找不到合适的物品以填满背包，则说明“刚刚”装入背包的那件物品“不合适”，应将它取出“弃之一边”，继续再从“它之后”的物品中选取；如此重复，直至求的满足条件的解，或者无解。由于回退重选规则就是“后进先出”规则，因此自然要使用堆栈。

数据结构：

/**堆栈的数据结构**/
typedef struct snode
{
    int weight;    /**定义权值**/
    int i;         /**定义在数组中的位置**/
    struct snode *next;
}LSnode;
/**背包的数据结构**/
typedef struct knapsack
{
    int Location;         /**定义数组内的位置**/
    int Choose_flag;      /**定义是否在堆栈标志位**/
    int Pop_flag;         /**定义是否出栈标志位**/
}pack;

 

首先我们先设计堆栈，分为堆栈初始化，判断堆栈是否为空函数，入栈，出栈，取栈顶元素，销毁堆栈几个操作函数，其代码如下：

/**stack.c**/
#include "stack.h"

/**堆栈初始化函数**/
void StackInitiate(LSnode **head)
{
    *head = (LSnode *)malloc(sizeof(LSnode));
    (*head)->next = NULL;
}
/**堆栈非空否函数**/
int StackNotEmpty(LSnode *head)
{
    if(head->next == NULL) return 0;
    return 1;
}
/**入栈函数**/
void StackPush(LSnode *head,int weight,int i)
{
    LSnode *PreNode;
    PreNode = (LSnode *)malloc(sizeof(LSnode));

    PreNode->next = head->next;
    PreNode->weight = weight;
    PreNode->i = i;
    head->next = PreNode;
}

/**出栈函数**/
int StackPop(LSnode *head,int *weight,int *i)
{
    LSnode *PreNode;
    PreNode = head->next;
    if(PreNode == NULL)
    {
        printf("Stack is empty!\n");
        return 0;
    }
    head->next = PreNode->next;
    *weight = PreNode->weight;
    *i = PreNode->i;
    free(PreNode);
    return 1;
}

/**取出栈顶元素函数**/
int StackTop(LSnode *head,int *weight,int *i)
{
    LSnode *PreNode;
    PreNode = head->next;
    if(PreNode == NULL)
    {
        printf("Stack is empty!\n");
        return 0;
    }
    *weight = PreNode->weight;
    *i = PreNode->i;
    return 1;
}
/**销毁栈顶元素**/
void Destroy(LSnode *head)
{
    LSnode *CurNode;
    LSnode *PreNode;

    CurNode = head;
    while(CurNode != NULL)
    {
        PreNode = CurNode;
        CurNode = CurNode->next;
        free(PreNode);
    }
}

相应的头文件如下：

/**stack.h**/
#ifndef _STACK_H
#define _STACK_H
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
typedef struct snode
{
    int weight;    /**定义权值**/
    int i;         /**定义在数组中的位置**/
    struct snode *next;
}LSnode;
void StackInitiate(LSnode **head);
int StackNotEmpty(LSnode *head);
void StackPush(LSnode *head,int weight,int i);
int StackPop(LSnode *head,int *weight,int *i);
int StackTop(LSnode *head,int *weight,int *i);
void Destroy(LSnode *head);
#endif // _STACK_H

 背包设计函数分为，结构体初始化，信息查询函数，信息赋值函数，权值打印函数，找寻权值组合函数，相应的注释都标在代码中：

/**knapsack.c**/
#include "knapsack.h"
/**初始化函数**/
void PackInitiate(pack array[],int n)
{
    int i;
    for(i = 0;i < n;i++)
    {
        array[i].Location = -1;
        array[i].Choose_flag = 0;
        array[i].Pop_flag = 0;
    }
}
/**信息查询函数**/
void ServiceInformation(pack array[],int i,int n,int *Choose_flag,int *Pop_flag)
{
    int j;
    for(j=0;j<n;j++)
    {
        if(array[j].Location == i)
        {
            *Choose_flag = array[j].Choose_flag;
            *Pop_flag = array[j].Pop_flag;
             break;
        }
    }
    if(j == n)
    {
        *Choose_flag = 0;
        *Pop_flag = 0;
    }
}
/**信息赋值函数，将Pop_flag置为输入的值**/
void EndowedInformation(pack array[],int i,int n)
{
    int j;
    for(j=0;j<n;j++)
    {
        if(array[j].Location == i)
        {
            array[j].Pop_flag = 1;
            break;
        }
    }
}
/**得到权值函数**/
void GetWeight(int Weightarray[],int n,int *GoalWeight)
{
    int i;
    printf("请输入目标权重:\n");
    scanf("%d",GoalWeight);
    printf("请输入%d个数据：\n",n);
    for(i=0;i<n;i++)
    {
        scanf("%d",&Weightarray[i]);
    }
}
/**打印权值函数**/
void Printweight(LSnode *head)
{
    int weight,weight_i;
    printf("权值如下：\n");
    while(StackNotEmpty(head))
    {
        StackPop(head,&weight,&weight_i);
        printf("%d ",weight);
    }
    printf("\n");
}
/**找到相应权值组合函数**/
int FindWeightCombination(int Weightarray[],int *GoalWeight,int n)
{
    LSnode *head;
    int i = 0;
    int weight_i;
    int count = 0;
    int weight = 0;             /**定义出栈权值**/
    int GoalWeightTemp = 0;     /**定义目标权重寄存值**/
    int Choose_flag = 0;
    int Pop_flag = 0;
    int push_flag;
    pack array[n];          /**定义一个数组存储已在堆栈里面**/
    StackInitiate(&head);   /**初始化堆栈**/
    PackInitiate(array,n);  /**初始化结构体变量**/
    StackPush(head,Weightarray[i],i); /**将第0项压入结构体**/
    push_flag = 1;                  /**另push_flag = 1,防止第一个权值二次入栈**/
    while(StackNotEmpty(head))
    {
        ServiceInformation(array,i,n,&Choose_flag,&Pop_flag);
        if(!Choose_flag && !Pop_flag && i<n)  /**当前位置的值是否被访问过**/
            GoalWeightTemp = GoalWeightTemp + Weightarray[i];

        if(GoalWeightTemp == *GoalWeight)      /**当找到权值组合的时候我们结束循环**/
        {
            if(!push_flag)                       /**防止第一个权值二次入栈**/
                StackPush(head,Weightarray[i],i);

            printf("Finding Weight goal successfully!\n");
            break;
        }
        else if(GoalWeightTemp < *GoalWeight && i < n && !Choose_flag && !Pop_flag) /**当前权值小于目标权值的时候我们将当前元素入栈**/
        {
            if(!push_flag)
                StackPush(head,Weightarray[i],i);
            array[count].Location = i;
            array[count].Choose_flag = 1;
            count++;

        }
        else if(GoalWeightTemp > *GoalWeight && i < n && !Pop_flag && !Choose_flag)/**当前权值大于目标权值的时候我们减掉当前元素**/
        {
             GoalWeightTemp = GoalWeightTemp - Weightarray[i];
        }
        else if(i == n && GoalWeightTemp != *GoalWeight)        /**当一遍权值试过之后无法得到相应的权值，说明当前栈顶的元素不合适，出栈**/
        {
            StackPop(head,&weight,&weight_i);   /**出栈**/
            EndowedInformation(array,weight_i,n);   /**将Pop_flag置1**/
            GoalWeightTemp = GoalWeightTemp - weight;
            i = 0;
            continue;
        }
        if(i<n) /**当i<n时i++**/
          i++;
          push_flag = 0;
    }

    if(GoalWeightTemp != *GoalWeight)
    {
        printf("无法找到相应的组合!\n");
        return 0;
    }
    Printweight(head);
    Destroy(head);
    return 1;
}

相应的头文件如下：

/**knapsack.h**/
#ifndef _KNAPSACK_H
#define _KNAPSACK_H
#include "stack.h"
typedef struct knapsack
{
    int Location;         /**定义数组内的位置**/
    int Choose_flag;      /**定义是否在堆栈标志位**/
    int Pop_flag;         /**定义是否出栈标志位**/
}pack;

void PackInitiate(pack array[],int n);
void ServiceInformation(pack array[],int i,int n,int *Choose_flag,int *Pop_flag);
void EndowedInformation(pack array[],int i,int n);
void GetWeight(int Weightarray[],int n,int *GoalWeight);
void Printweight(LSnode *head);
int  FindWeightCombination(int Weightarray[],int *GoalWeight,int n);

#endif // _KNAPSACK_H

最终的主函数如下：

/**main.c**/
#include "stack.h"
#include "knapsack.h"
int main()
{
    int n;            /**定义个数**/
    int GoalWeight;   /**定义目标权值**/
    int i,j;
    int curtemp,pretemp;         /**定义缓存值**/
    printf("请输入物体个数：\n");
    scanf("%d",&n);
    if(n<0)
    {
        printf("输入错误！\n");
        exit(0);
    }
    int Weightarray[n];    /**定义权值数组**/
    GetWeight(Weightarray,n,&GoalWeight); /**输入相应信息**/
    for(i=0;i<n;i++)
    {
        printf("以权值%d为栈底时：\n",Weightarray[0]);
        FindWeightCombination(Weightarray,&GoalWeight,n);/**输出权值组合**/
        /**这里我们将每个输入的权值进行圆周循环，找到所有的权值集合**/
        for(j=0;j<n;j++)
        {
            if(j==0)
            {
                curtemp = Weightarray[j+1];
                Weightarray[j+1] = Weightarray[j];
            }
            else if(j<n-1)
            {
                pretemp = Weightarray[j+1];
                Weightarray[j+1] = curtemp;
                curtemp = pretemp;
            }
            else
            {
                Weightarray[0] = curtemp;
            }
        }
    }

    return 0;
}

最终运行结果如下图：

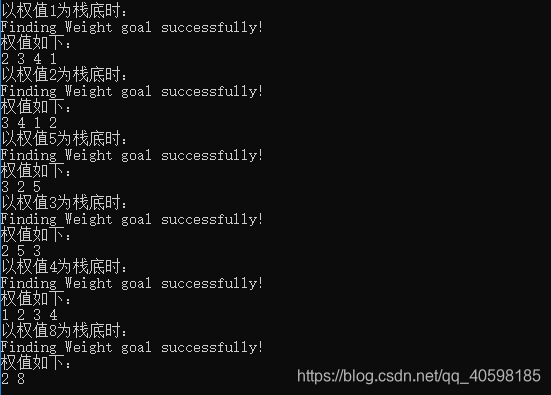
完。