排序之希尔排序

希尔排序思想

希尔排序对要排序的数字进行分组，在组内进行排序。排序完成需要进行多次分组，每次分组的个数是前一次分组个数的一半。

 

图示

以 [3  2  9  0  6  1  5  4  8  7] 该数组为例从小到大进行排序。

1. 首先将该组数字进行分组，首次分组的个数为数组长度除以2，即 10 / 2 = 5 组，下面相同颜色的为一组（即同一组内数字之间的下标的距离为组的个数）。

2. 将数字在各自组内进行排序，得到下面的结果

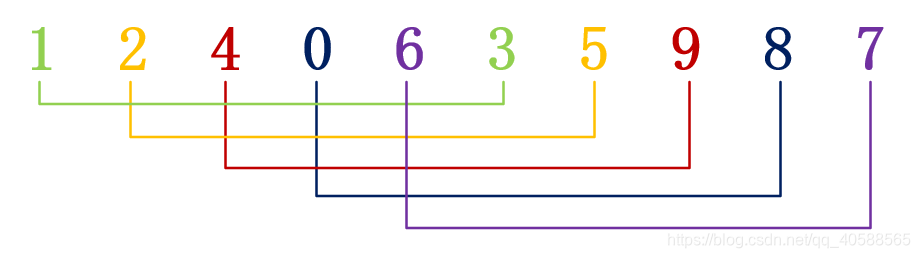
3.排序之后再次进行分组，分组的个数为前一次分组个数除以 2，即5 / 2 = 2组 （结果不为整数便向下取整）

4. 将数字在各自组内进行排序，得到下面的结果

5. 再次进行分组，分组的个数为前一次分组个数除以 2，即2 / 2 = 1组，分组个数为1也就是整个数组。对整个数组排序之后便得到最终的排序结果。

总结：

从以上步骤可以看出，采用希尔排序也就是把整个数组分成若干组，然后在组内进行排序。随着分组数目减小直到变为1时，便是对整个数组排序，也是该步骤后得到最后的排序结果。当然组内的排序可以使用交换法，或者插入法等。

希尔排序的出现主要是为了解决插入排序的缺陷，当使用插入排序时（从小到大排序），如果在一组数字中，小的数字都相对靠右边，这无疑增加了比较和移位的次数，使得耗费时间增加。从上述图示步骤中可以看出，采用希尔排序可以尽早的将靠在右边的小的数字挪到前面，这样可以极大的提高插入排序的效率。希尔排序主要还是搭配插入法来完成排序。

 

代码实现

希尔排序（交换法）

public static void shellSort(int[] array) {
        //定义临时变量，交换时使用
        int temp;
        //获取数组长度
        int num = array.length;
        //定义步长
        int step;

        while (num > 1) {
            num /= 2;
            //让步长等于每次分组的个数
            step = num;
            for (int i = 0; i < array.length - step; i++) {
                for (int j = i + step; j < array.length; j += step) {
                    if (array[j] < array[i]) {
                        temp = array[i];
                        array[i] = array[j];
                        array[j] = temp;
                    }
                }
            }
        }
    }

希尔排序（插入法）

public static void shellSort2(int[] array) {
        //获取数组长度
        int num = array.length;
        //定义步长
        int step;

        while (num > 1) {
            num /= 2;
            //让步长等于每次分组的个数
            step = num;
            for (int i = step; i < array.length; i++) {
                int insertValue = array[i];
                int compareIndex = i - step;
                while (compareIndex >= 0 && array[compareIndex] > insertValue) {
                    array[compareIndex + step] = array[compareIndex];
                    compareIndex -= step;
                }
                array[compareIndex + step] = insertValue;
            }
        }
    }