【中级软考—软件设计师】1计算机组成与体系结构1.1数据的表示【****】：1.1.3浮点数表示

教学链接
软考重点预知：
本章主考概念内容——掌握特点小节

浮点数的概念

【需掌握】：格式，各个组成部分的特点和意义，浮点数运算的逻辑过程(尤其是对接的过程)，
【了解】：实际的运算

浮点数的运算

浮点数表示：

几个数的表示形式：

• 指数(阶码)一般用移码来表示
• 基数在计算机中不需要存储的
• 尾数一般用补码来表示
  • 特殊情况：有一类特殊的标准IEEE 754——这一部分的尾数可以用原码来表示

阶码和尾数的意义存在

阶码：

• 用来判断数值的大小
  尾数：
  • 可以表示数值的有效精度，长度越大，位数越多，精度越准确

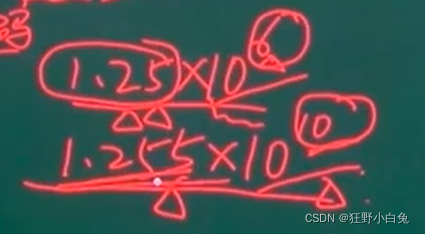
运算过程：

• 对阶——尾数计算——结果格式化【二进制当中的】

例：对上述浮点数做加法运算

步骤：

1、让他们的阶码对齐——称为对阶

注：对齐6——错的

• 一般都是小数向大数看齐
• 对阶是通过较小数的尾数右移实现的
  • 右移的过程当中，如果有符号位的话，符号位保持不变——这种称为算术右移
    

2、尾数计算

阶码扩大了一万倍，尾数就要缩小一万倍

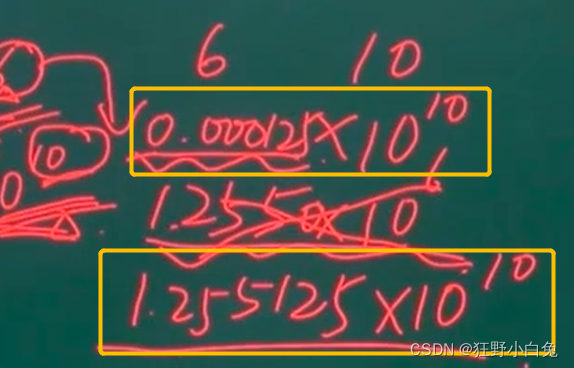
3、结果格式化【二进制当中】

我们在二进制当中，进行浮点数运算的时候，还需要对结果进行格式化

• 将我们的尾数限定在0.5-1之间

特点【重点掌握】

例题讲解

例1—考察：浮点数表示

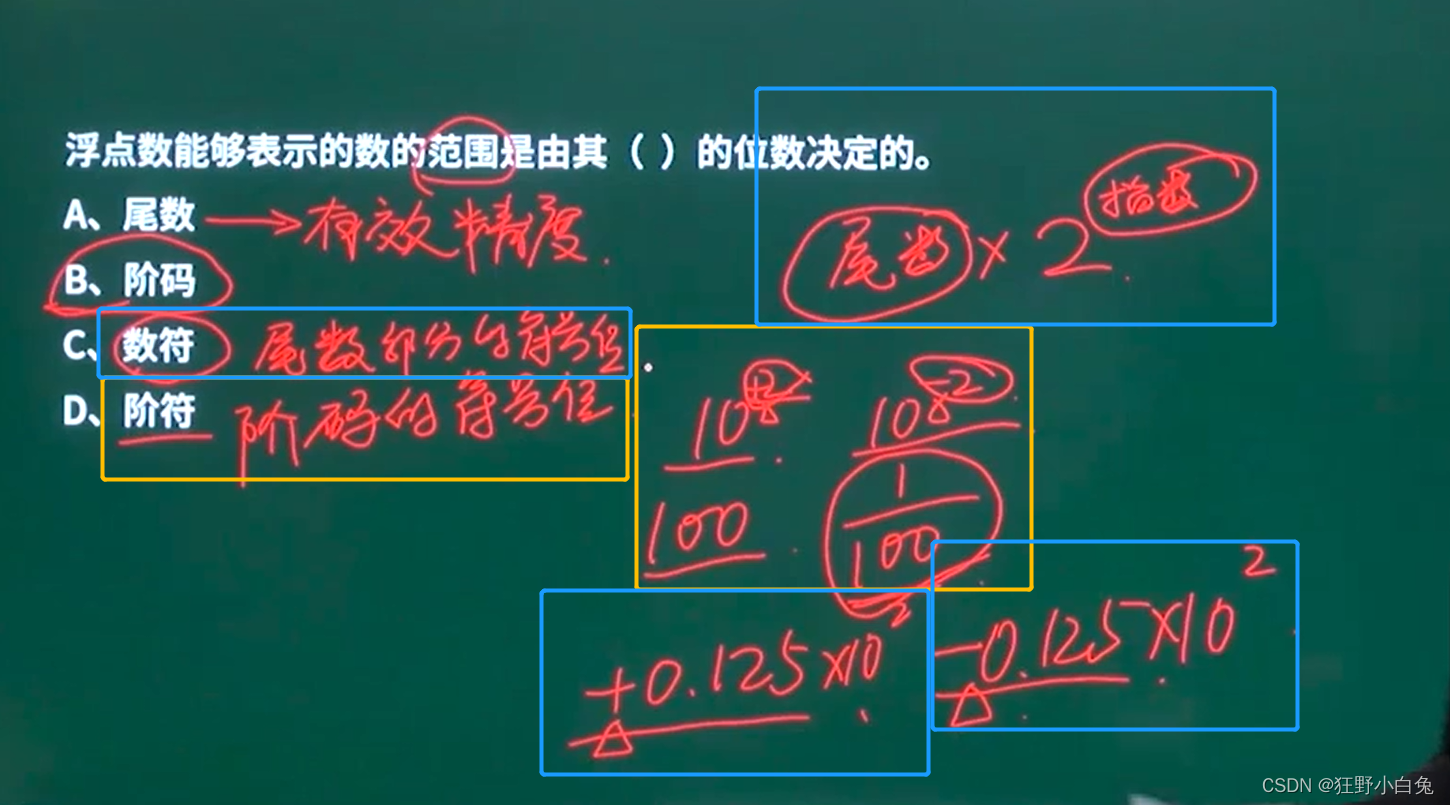
• 选B

例2—考察：运算过程

• 选B

例3—考察：浮点数结构，码制当中移码和补码数值的表示范围【定点小数】【难题】

• 选B
• 移码当中的【人为定义】
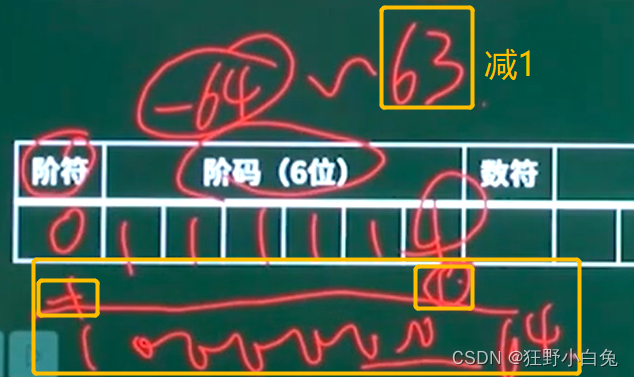
  • 最小范围：阶符取1，阶码全0—将-0的编码利用起来了得到-64【具体看教学链接】
    
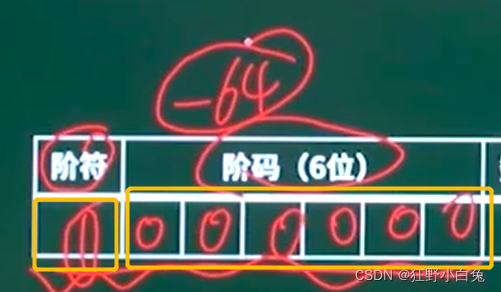
  • 最大范围：阶符取0，阶码全1—补正计算(先加1然后减1)得到：63
    
• 补码当中的【人为定义】
  • 补码表示，尾数可以用-1