【2024.8.17】【米哈游】【软开笔试】编程题三道

此为笔者朋友所做笔试，拿来复盘一下
整体并没有很复杂的数据结构使用

5.1 原石

贪心，具体来说

• 对于每个三十天，买月卡一定是最值的（因为月卡返现就1元10原石）
• 因此，画出状态树即可知道怎么做
  

#include<stdio.h>
#include<iostream>
using namespace std;
int main() {
	int n, m;
	cin >> n >> m;
	// 直接买满月卡（例如有32天只买一个月卡），所能获得的原石，以及其基础花费
	int cur = m / 30 * 300 + m/30*30 * 90; 
	int cost = m / 30 * 30;
	// 月卡原石不够
	if (n > cur) {
        // 直接花钱补足原石
		int plana = (n - cur) / 10;
        
        // 额外购买一张月卡之后的原石缺口
		int _ = (n - cur - 300 - m % 30 * 90);
        // 购买一张月卡正好补足原石缺口
		if (_ <= 0) {
			if (plana > 30) {
				cost += 30;
			}
			else {
				cost += plana;
			}
		}
        // 购买一张月卡不足以补足原石缺口，此时贪心做法直接用钱补足（因为每日90原石已经没法用了）
		else {
			int planb = _ / 10 + 30;
			cost += plana > planb ? planb : plana;
		}
	}
    // 月卡原石够了，考虑不买月卡的情况（实际上根本不用比较）
	else {
		int plana = n / 10;
		cost = cost < plana ? cost : plana;
	}

	cout << cost << endl;
	
}

5.2 区间

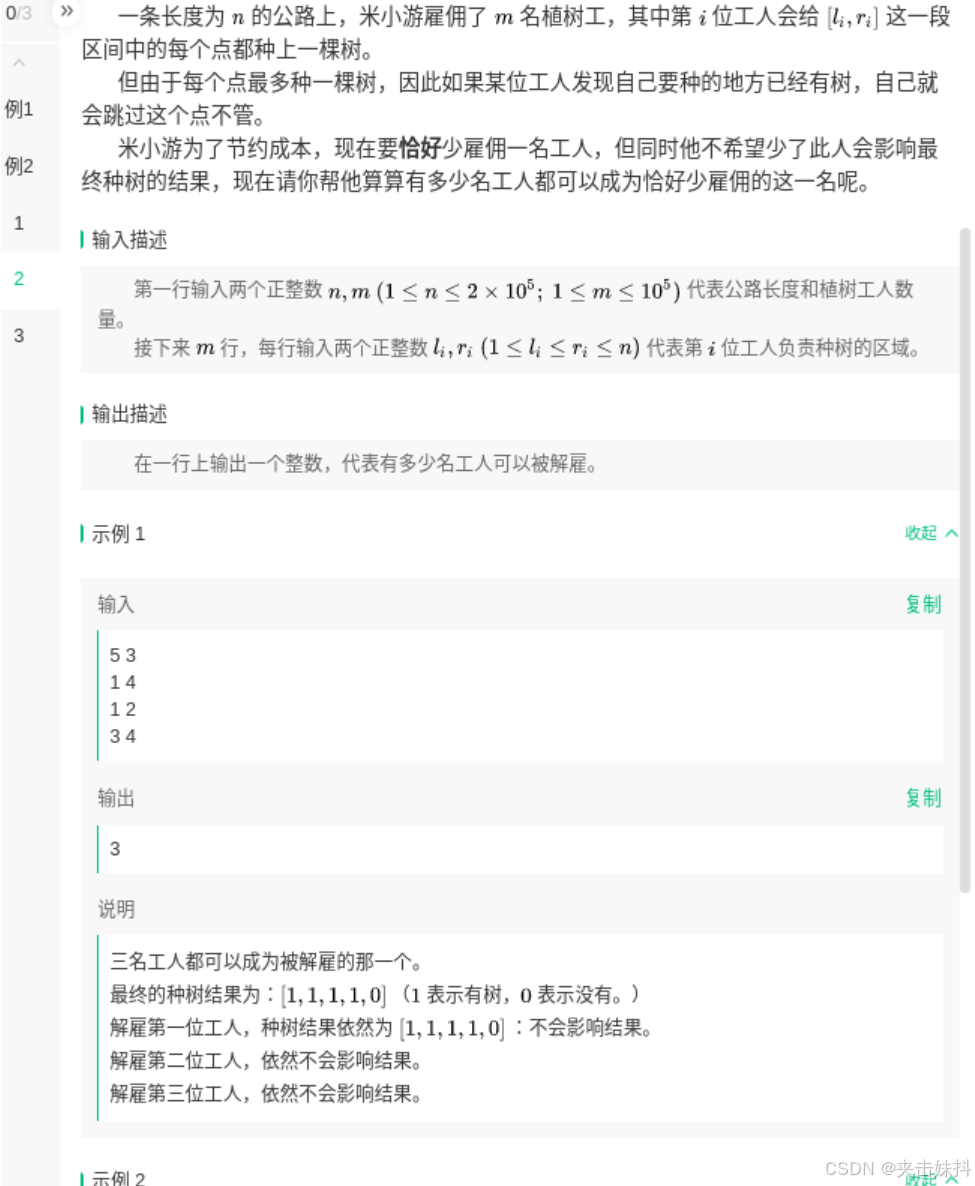
这道题目的第一想法就是，记录一个road数组，这个数组表示每个位置的树可能被栽种多少次，多于一次的必然是可以削减的，我们只需要寻找那些只被栽种了一次的情况即可。也就是，找到这些种树的位置，然后寻找对应的工人（看谁是负责这棵树的）

如果使用暴力，那么最坏情况就是1e5*2e5，超时。超时的主要点在于工人存储的是一个区间，也就是我们可能需要遍历知道哪个工人负责这一颗树（并且每个点都要查一遍）

例如，有n-1个工人，他们负责第一棵树，最后一个工人负责其他所有树

那么，就算使用二分法，也是log(1e5) * 2e5,实际上也是2e9应该会超时

因此，我们需要一个新的方法，使用这个点，以及找到对应的工人

换一个思路，我们能否查询每个工人管辖的区域内是否包含独苗(road=1)呢

显然是可以的，因为是访问数组，因此是1e5次O(1)操作

考虑到工人存储的是区间，能否有一个方法快速利用区间查询达到O(1)查询的效果呢

显然也是有的，因为是连续区间，第一时间就能想到前缀和。

不过road数组需要改变一下：road[i] == 1代表第i个位置为独苗，否则road[i] == 0

那么，前缀和数组的意义就在于，工人给出[r,l]的范围，如果其road[l]-road[r]==0，这就代表在这段区间内一定没有独苗，也就是这个工人是可替代的。

笔者一开始想通过对工人的区间排序（起始位置从小到大，终止位置从大到小），然后贪心的做。具体来说，维护一个到当前工人位置，最远的树苗在哪，然后在这个树苗位置被更新前，所有终止位置小于等于该树苗的工人都是可以被替代的（因为起始位置从小到大保证了这一点，在每个判断时刻，我们都能人为这段区间是都种的上树苗的）

这个问题有一个很大的漏洞，也就是题目所给的[1,2][3,4][1,4]，这个方法没有认为[1,4]是可替代的

因此，我也想过动态规划，但是没想出来

#include<stdio.h>
#include<iostream>
#include<vector>
#include<algorithm>
#include<unordered_map>
using namespace std;
int main() {
	int n, m;
	cin >> n >> m;

	vector<pair<int, int>> range(m);
	vector<int> road(n+1, 0);
    // 读取输入，并维护road
	for (int i = 0; i < m; i++) {
		cin >> range[i].first >> range[i].second;

		for (int j = range[i].first; j <= range[i].second; j++) {
			road[j]++;
		}
	}


	// 更新road为前缀和
	for (int i = 0; i <= n; i++) {
		if (road[i] > 1) road[i] = 0; else road[i] = 1;

		if(i > 0)
			road[i] += road[i - 1];

		//cout << road[i] << "\t";
	}
    // 判断每个工人，哪些工人是可替代的。
	int cnt = 0;
	for (int i = 0; i < range.size(); i++) {
		if (road[range[i].second] - road[range[i].first] == 0) {
			cnt++;
			//cout << cnt << endl;
		}
	}
	cout << cnt << endl;


}

5.3 子数组

这一题笔者来不及做了

一看很简单，如果不考虑超时

我们首先判断所给区间内所有符合的值的下标并记录到index数组中

我使用的是暴力，也就是遍历区间，实际上这很容易超时

我们可以维护一个map，map[value] = vector

这里的value是数组中的值，vector记录了他们的下标，这样应该会好很多

通过这些下标我们应该可以得到子数组的规律，对于每个值x分别是

• 以x为head，非x为tail的数组（长度必须大于1）

• 以x为tail，非x为head的数组（长度必须大于1）

  以上两个都可以根据此处查询区间的l,r和当前计算到的x所对应下标，以及后面拥有的x个数来判断

  

• 仅含有x自身的数组

• 同时以x为head和以x为tail的数组(其实就是首项加尾项乘项数除以2，(index.size()-1+1)*(index.size()-1)/2，比如你有四个值和x相同，下标分别是[1,3,5,7]，那么一共有[1,3][1,5][1,7][3,5][3,7][5,7]这么多种)

• 以非x为head，非x为tail但是包含x的数组

我们需要在遍历到index中每个x时，按顺序这样将可用的nonx组合，以避免重复子数组和非法子数组（指子数组中没有x）

这样做（x之前的每个和x之后的每个配对）保证了子数组一定含有x。

并且显然，不会遗漏

代码并没有很多用例测试，可能含有bug

#include<stdio.h>
#include<iostream>
#include<vector>
#include<algorithm>
#include<unordered_map>
using namespace std;
int main() {
	int n;
	cin >> n;

	vector<int> nums(n);

	for (int i = 0; i < n; i++) {
		cin >> nums[i];
	}



	int q;
	cin >> q;

	for (int i = 0; i < q; i++) {
		int l, r, x;
		cin >> l >> r >> x;
		l--;
		r--;
		bool find = false;
		vector<int> index;
		for (int j = l; j <= r; j++) {
			if (nums[j] == x) {
				find = true;
				index.push_back(j);
			}
		}
		int cnt = 0;
		int nonxbegin = 0;
		for (int j = 0; j < index.size(); j++) {
			// x as head and > 2 and nonx as tail
			cnt += r - index[j] - (index.size() - 1 - j);
			// x as tail and > 2 and nonx as head
			cnt += index[j] - l - j;

			// nonx as head and nonx as tail
			if (nonxbegin < index[j]) {
				int front = index[j] - nonxbegin;
				int back = r - index[j] - (index.size() - 1 - j);

				cnt += front * back;
			}
			nonxbegin = index[j] + 1;

		}

		// x as tail and as head
		cnt += (index.size() - 1 + 1) * (index.size() - 1) / 2;
		// only x
		cnt += index.size();




		cout << cnt << endl;
	}
	
	


}

总结

米哈游没有像华为和携程那样考动态规划和图论，而是都是可以通过找规律解答的题目，总体来说时间可能对于笔者有些紧凑，很好奇其他岗位是否也是这样考
此处前两题确定A，最后一题没来得及提交。