三、(数据分析)-数据清洗----缺失值处理

数据清洗之缺失值处理–拉格朗日插值法、牛顿插值法

在数据数据分析的工作中，数据清洗主要是删除原始数据集中的无关数据，重复数据，平滑噪声数据，筛选掉与挖掘主题无关的数据，处理缺失值，异常值等。

1、缺失值处理
处理缺失值的方法可以分为3类：删除记录，数据插补和不处理，其中常用的数据插补方法右以下几种。

插补方法	方法描述
均值/中位数/众数插补	根据属性值的类型，用该属性取值的平均数/中位数/众数进行插补
使用固定值	将缺失的属性值用一个常量进行替换，比如某地的基本工资可以用来作为插补值
最近插补	在记录中找到与缺失样本最接近的样本的该属性值进行插补
回归方法	对带有缺失值的变量，根据已有的数据和与其相关的其他变量的数据建立拟合模型来预测缺失值的属性值
插值法	插值法是利用已知点建立合适的插值函数，未知值由对应点xi求出的函数值f(xi)近似代替

如果通过简单的删除小部分记录达到既定的目标，那么删除含有缺失值的记录是最有效的方法，然而这种方法却有很大的局限性，它是以减少历史数据来换取数据的完备，会造成资源的大量浪费，将丢弃了大量隐藏在这些记录中的信息。尤其是在包含很少数据的情况下，删除少量的记录将会严重影响到分析结果的客观性和正确性，一些模型可以将缺失值视作一种特殊的取值，允许直接在含有缺失值的数据上进行建模。我们将介绍拉格朗日插值法和牛顿插值法。

2、拉格朗日插值法
根据数学公式可知，在一个平面上有n个点，那么可以找到一个n-1次的多项式，使得这个多项式过这n个点，我们可以根据这个原理去预测以下缺失值。

假设多项式：
$$y=a^0+a^{1}x+a^2{x}^2+.....+a^{n-1}{x}^{n-1}$$
将n个点的坐标(x1, y1),(x2, y2)…,(xn, yn)带入得：
$$y_1=a_0+a_1{x}_1+a_2{x}_1^2+.....+a_{n-1}{x}_1^{n-1}$$
$$y_2=a_0+a_1{x}_2+a_2{x}_2^2+......+a_{n-1}{x}_2^{n-1}$$
$$y_n=a_0+a_1{x}_{2}n+a_2{x}_n^2+......+a_{n-1}{x}_n^{n-1}$$

解出拉格朗日插值多项式：
$$L(x)=y_1\frac{(x-x2)(x-x3)...(x-x_n)}{(x_1-x_2)(x_1-x_3)...(x_1-x_n)}+y2\frac{(x-x_1)(x-x_3)...(x-x_n)}{(x_2-x_1)(x_2-x_3)...(x_2-x_n)}+......+y_n\frac{(x-x_1)(x-x_2)...(x-x_{n-1})}{(x_n-x_1)(x_n-x_2)...(x_n-x_{n-1})}$$
$$=\sum _{i=0}^n{y}_i\prod _{j=0,i!=i}^n\frac{x-x_j}{x_i-x_j}$$

将缺失的函数值对应的点x带入插值多项式得缺失值的近似值L(x)。

拉格朗日插值公式结构紧凑，在理论分析中很方便，但是当插值节点递减时，插值多项式就会随之变化，这在实际的计算中是很不方便的，为了克服这一缺点，于是提出了牛顿插值法。

3、牛顿插值法
求已知的n个点对$$(x^1,y^1),(x^2,y^2),(x^3,y^3),...(x^n,y^n)$$的所有阶差商公式：
$$f[x_1,x]=\frac{f[x]-f[x_1]}{x-x_1}=\frac{f(x)-f(x_1)}{x-x_1}$$
$$f[x_2,x_1,x]=\frac{f[x_1,x]-f[x_2,x_1]}{x-x_2}$$
$$f[x_3,x_2,x_1,x]=\frac{f[x_2,x_1,x]-f[x_3,x_2,x_1]}{x-x_3}$$
$$f[x_n,x_{n-1},...,x_1,x]=\frac{f[x_{n-1},...,x_1,x]-f[x_n,x_{n-1},...,x_1]}{x-x_n}$$

联立以上差商公式建立如下插值多项式f(x)
$$f(x)=f(x_1)+(x-x_1)f[x_2,x_1]+(x-x_1)(x-x_2)f[x_3,x_2,x_1]+(x-x_1),(x-x_2)(x-x_3)f[x_4,x_3,x_2,x_1]+...$$$$+(x-x_1)(x-x_2)...(x-x_n)f[x_n,x_{n-1},...,x_1,x]$$$$=P(x)+R(x)$$
其中
$$P(x)=f(x_1)+(x-x_1)f[x_2,x_1]+(x-x_1)(x-x_2)f[x_3,x_2,x_1]+$$$$(x-x_1)(x-x_2)(x-x_3)f[x_4,x_3,x_2,x_1]+...+(x-x_1)(x-x_2)...(x-x_{n-1})f[x_n,x_{n-1},...x_2,x_1]$$
$$R(x)=(x-x_1)(x-x_2)...(x-x_n)f[x_n,,x_{n-1},x_1,x]$$

R(x)是牛顿插值逼近函数，R(x)是误差函数
将缺失的函数值对应的点x带入插值多项式得到缺失值的近似值f(x)

牛顿插值法也是多项式插值，但采用了另一种构造插值多项式的方法， 与拉格朗日插值相比，具有承袭性和易于变动节点的特点，从本质上来说，两者给出的答案是一致的(相同的次数，相同系数的多项式)， 只不过表示的形式不同，因此，在Python中Scipy库中，只提供了拉格朗日插值法的函数的使用， 如果需要牛顿插值法，则需要自己编写函数的实现。

4、下面介绍案例实现拉格朗日插值的实现方法

在餐饮系统中的销售量可能会出现缺失值，我们使用拉格朗日插值法对缺失的数据进行填补。

时间	2015/2/25	2015/2/24	2015/2/23	2015/2/22	2015/2/21	2015/2/20
销售额	3442.1	3393.1	3136.6	3744.1	6607.4	4060.3

时间	2015/2/19	2015/2/18	2015/2/16	2015/2/15	2015/2/14	2015/2/13
销售额	3614.7	3295.5	2332.1	2699.3	空值	3036.8

import pandas as pd

from scipy.interpolate import lagrange

inputfile = '../data/catering_sal.xls'
outfile = '../tmp/sales.xls'

data = pd.read_excel(inputfile)
# 过滤异常值，将其变为空值
data['销量'][(data['销量'] < 400) | (data['销量'] > 5000)] = None

# 自定义列向量插值函数
# s为列向量， n为被插值的位置， k为取前后的数据个数，默认为5
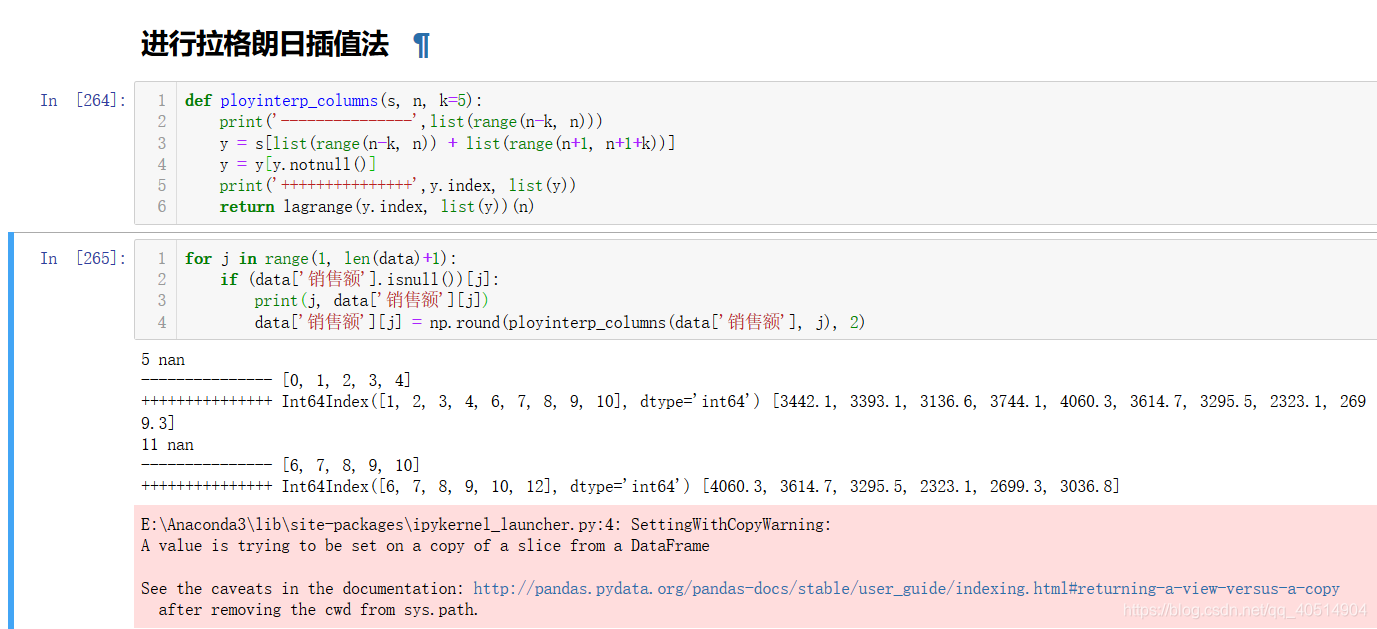
def ployinterp_columns(s, n, k=5 ):
	y = s[list(range(n-k, n)) + list[range(n+1, n+1+k)]] #取数
	y = y[y.notnull()] # 剔除空值
	return lagrange(y.index, list(y))(n) # 插值并返回插值结果

# 逐个元素判断是否需要插值
for i in data.columns:
	for j in range(len(data)):
		if (data[i].isnull())[j]: # 如果为空即插值
			data[i][j] = ployinterp_column(data[i], j)
data.to_excle(outputfile) # 输出结果，写入文件

使用拉格朗日插值法对缺失值进行插补，使用缺失值前后5个未缺失的数据参与建模，在进行插值之前，会对数据进行异常值检测，发现2015/2/21日的数据是异常的（数据大于5000）， 所以把该日期数据定义为空缺值，利用拉格朗日插值对2015/2/21， 2015/2/14的数据进行插补，结果是4275.255和4156.86， 这两天使周末，而周末的销售额一般要大于周一到周五的值，所以插值的结果比较符合实际情况。

---

望您：
“情深不寿，强极则辱，谦谦君子，温润如玉”。