递归DFS找出有向图中所有的环（Python）

借鉴：https://blog.youkuaiyun.com/iteye_8466/article/details/82440433

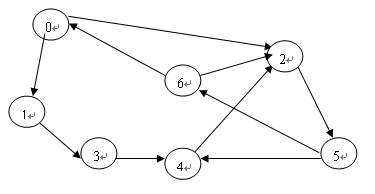
child_graph = {"0": "1#2", "1": "3", "2": "5", "3": "4",
                "4": "2", "5": "4#6", "6": "0#2"}

visited = []
trace = []
has_circle = False


def dfs(node_index):
    global has_circle
    if (node_index in visited):
        if (node_index in trace):
            has_circle = True
            trace_index = trace.index(node_index)
            for i in range(trace_index, len(trace)):
                print(trace[i] + ' ', end='')
            print('\n', end='')
            return
        return

    visited.append(node_index)
    trace.append(node_index)

    if(node_index != ''):
        children = child_graph[node_index].split('#')
        for child in children:
            dfs(child)
    trace.pop()


dfs("1")
if(has_circle == False):
    print("No Cycle.")

输出结果：

4 2 5 
1 3 4 2 5 6 0 
2 5 6 0 
2 5 6 

另外，该算法的结果与深度优先搜索的起始点有关，例如，在上例中，如果起始点为"0"，则只能找出3个环。不同起始点可能造成结果不同。

再看一个例子：

将上述代码中的child_graph改一下：

child_graph = {"0": "1#5", "1": "2", "2": "3#4", "3": "0",
                "4": "", "5": "6", "6": "0"}

然后起始点为"0"：

dfs("0")

输出结果为：

0 1 2 3 
0 5 6 

可见，结果正确。

但如果起始点为"4"：

dfs("4")

则结果为：

No Cycle.

由图中可以看出，"4"号点已经没有子节点，所以DFS以该点为起点的话，没有办法遍历整个图，所以没有办法找出环。

这也是为什么程序的运行结果与起始点有关。