c++深度寻路算法

最新推荐文章于 2023-03-25 14:43:54 发布

原创最新推荐文章于 2023-03-25 14:43:54 发布 · 248 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#深度寻路

c++笔记专栏收录该内容

29 篇文章

订阅专栏

本文介绍如何使用C++实现深度优先搜索（DFS）算法，通过栈来管理路径，并处理地图上的方向变化，同时避免重复走过的路线。深度优先搜索是一种在图形或树结构中寻找路径的有效方法。

通过栈来存储路径，辅助地图更改方向与记忆路是否走过

#include <iostream>
#include <stack>
#include <Windows.h>
using namespace std;
#define ROWS 12//x
#define COLS 12//y
struct MyPoint {
	int x;
	int y;
	//MyPoint(int xx, int yy) :x(xx), y(yy) {};
};
//辅助地图
enum dirent{p_up, p_left, p_down, p_right};
struct pathNode {
	int val;//
	dirent dir;	//方向
	bool	isFind;//是否走过
	
};

//打印地图
void printMap(int map[][12], MyPoint pos)
{
	system("cls");
	for (int i = 0; i < ROWS;i++)
	{
		for (int j = 0; j < COLS;j++)
		{
			if (i == pos.x && j == pos.y)
			{
				cout << "#";
			}
			else if (map[i][j])
			{
				cout << "*";
			}
			else
			{
				cout << " ";
			}
		}
		cout << endl;
	}
	Sleep(200);
}
int main()
{
	/*
	地图：  数组
	1墙  0路
	*/
	int map[ROWS][COLS] = {
		{1,1,1,1,1,1,1,1,1,1,1,1},
		{1,0,1,1,1,1,1,1,1,1,1,1},
		{1,0,1,1,0,1,1,1,1,1,1,1},
		{1,0,1,1,0,1,1,1,1,1,1,1},
		{1,0,1,1,0,1,1,0,0,0,0,1},
		{1,0,1,1,0,1,1,1,1,1,0,1},
		{1,0,0,0,0,0,0,0,1,1,0,1},
		{1,0,1,1,0,1,1,0,1,1,0,1},
		{1,0,1,1,0,1,1,0,1,1,0,1},
		{1,0,1,1,0,1,0,0,0,0,0,1},
		{1,0,1,1,0,1,0,1,1,1,0,1},
		{1,1,1,1,1,1,1,1,1,1,1,1}
	};
	MyPoint begPos = { 1,1 };
	MyPoint endPos = { 10,10 };
	//printMap(map,begPos);
	pathNode pathMap[ROWS][COLS] = { 0 };
	for(int i=0;i<ROWS;i++)
		for (int j = 0; j < COLS; j++)
		{
			pathMap[i][j].val = map[i][j];
		}
	MyPoint currentPos = begPos;
	MyPoint searchPos; //试探点
	stack<MyPoint> stack;
	stack.push(begPos);
	pathMap[begPos.x][begPos.y].isFind = true;//标记走过

	bool isFindEnd = false;
	while (!isFindEnd)
	{
		printMap(map,currentPos);
		//确定试探点
		searchPos = currentPos;
		switch (pathMap[currentPos.x][currentPos.y].dir)
		{
		case p_up:
			searchPos.x--;
			pathMap[currentPos.x][currentPos.y].dir = p_left;
			break;
		case p_left:
			searchPos.y--;
			pathMap[currentPos.x][currentPos.y].dir = p_down;
			break;
		case p_down:
			searchPos.x++;
			pathMap[currentPos.x][currentPos.y].dir = p_right;
			break;
		case p_right:
			searchPos.y++;
			if (pathMap[searchPos.x][searchPos.y].val != 0||	//不是路
				pathMap[searchPos.x][searchPos.y].isFind==true) //以前路过
			{
				stack.pop();
				currentPos = stack.top();
			}
			break;
		}
		//判断试探点
		if (pathMap[searchPos.x][searchPos.y].val==0&&	//路
			pathMap[searchPos.x][searchPos.y].isFind==0)	//未走过
		{
			
			currentPos = searchPos;
			//走
			//标记走过
			pathMap[currentPos.x][currentPos.y].isFind = true;
			//入栈
			stack.push(currentPos);
		}

		//判断是否终点
		if (currentPos.x == endPos.x &&
			currentPos.y == endPos.y)
			isFindEnd = true;
		//判断是否栈为空
		if (stack.empty())
		{
			cout << "未找到路径" << endl;
			break;
		}
	}
	//显示路径
	if (isFindEnd)
	{
		cout << "path:";
		while (!stack.empty())
		{
			cout << stack.top().x <<","<< stack.top().y << endl;
			stack.pop();
		}
	}
	return 0;
}

结果：

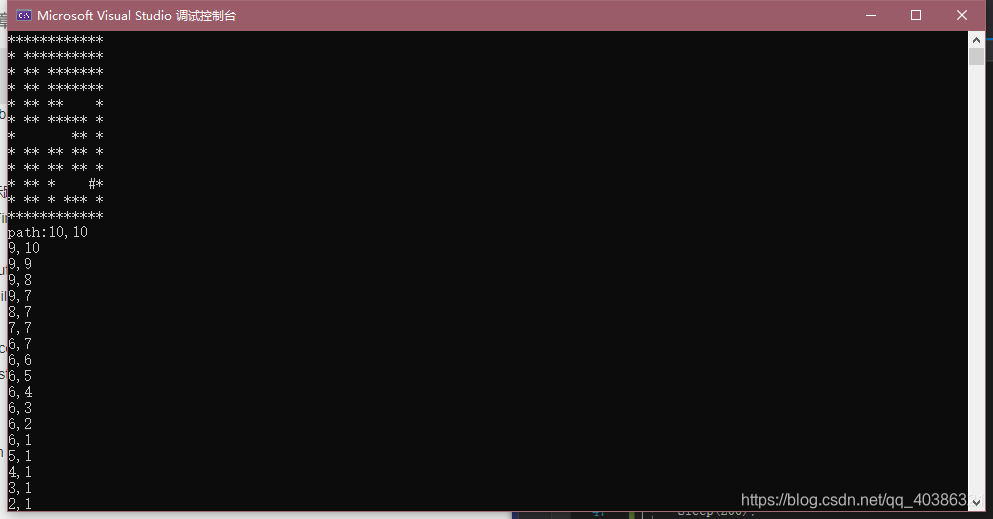
在这里插入图片描述