数据结构 - 树与二叉树 （C++）

一. 树的基本概念
 树（Tree）是n（n>=0）个结点的有限集。它有唯一的根（1结点）和若干颗互不相交的子树（如图上子树5、11、12等）组成。

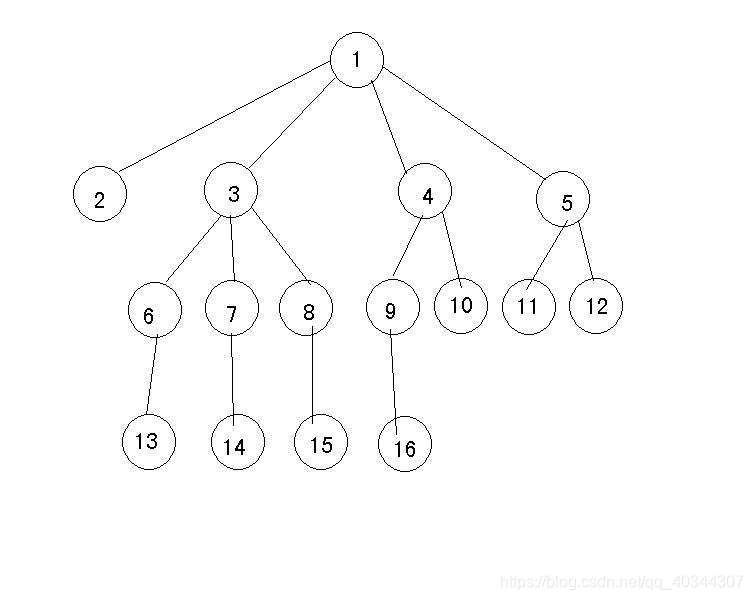
 接下来以上面树为例子介绍树的基本术语。

• 结点：1、2、3等都是结点，每个结点包含数据元素还有指向子树的分支。
• 结点的度：结点拥有的子树的数。（如：5结点的度为2）
• 树的度：树种各结点度的最大值。（如：上述树的度为3，即为3结点的度）
• 叶子结点：度为0的结点，也叫终端结点。（如：2、13、14等）
• 非终端结点：度不为0的结点，也叫分支结点。（如：3、7、9等）
• 孩子：结点子树的根。（如：1的孩子为2、3、4、5）
• 双亲：与孩子结点相对应。（如：2、3、4、5结点的双亲都是1结点）
• 兄弟：同一个双亲的孩子之间互为兄弟。（如：2、3、4、5互为兄弟）
• 祖先：从根到某一结点路径上的全部结点。（如：对路径1、5、11，1和5都是11的祖先）
• 子孙：以某结点为根的子树中的所有结点，都是该结点的子孙。（如：4的子孙是9、10、16）
• 层次：从根开始，每层子树算作一层。
• 树的高度（或深度）