深度学习笔记（三）

线性回归的简洁实现

在上一章的基础上，将介绍如何使用MXNet提供的Gluon接口方便实现线性回归

上一章： https://blog.youkuaiyun.com/qq_40318498/article/details/94716861

---

生成数据集

num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 4.2
features = nd.random.normal(scale=1,shape=(num_examples,num_inputs))
labels = true_w[0]*features[:,0] + true_w[1]*features[:,1] + true_b

读取数据集

Gluon提供data包来读取数据。特征数据和标签我们先生成好

from  mxnet.gluon import data as gdata
batch_size = 10
#将训练数据的特征和标签组合
dataset = gdata.ArrayDataset(features,labels)
#随机读取小批量,shuffle随机读取.入口参数（训练数据，一次性读取大小，随机）
data_iter = gdata.DataLoader(dataset,batch_size,shuffle=True)
for X,y in data_iter:
    print (X,y) #打印数据

定义模型

首先，导入nn模块(neural networks神经网络)，接着定义一个模型变量net,它是一个Sequential实例,Sequential实例可以看作一个串联各个层的容器。
当给定输入数据时，容器中的每一层将一次计算并将输出作为下次的输入。

from mxnet.gluon import nn
net = nn.Sequential()
net.add(nn.Dense(1))

在Gluon层中，全连接是一个Dense实例（线性回归中，两个输入层，一个输出层），我们定义该层输出个数是1,我们不需要指定每一层的输入的形状，因为模型会自动推断出每一层的输入个数。

初始化模型参数

我们需要从MXNet中导入init模块，通过init.Normal(sigma=0.01)指定权重参数每个元素将在初始化时随机采样于均值为0，标准差为0.01的正态分布。偏差默认初始化为0。**

from mxnet import init
net.initialize(init.Normal(sigma=0.01))

定义损失函数

在Gluon中，loss模块定义了各种损失函数，这里，我们使用平方损失函数

from mxnet.gluon import loss as gloss
loss = gloss.L2Loss() #平方损失又称为L2范数损失

定义优化算法

在导入Gluon后，我们创建一个Trainer实例，并指定学习率为0.03的小批量随机梯度下降(sgd)为优化算法，该优化算法用来迭代net实例所有通过add函数嵌套的层所包含的参数。这些参数可以通过collect_params函数获取

from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.03})

训练模型

通过调用Trainer实例的step函数来迭代模型参数，变量l是长度为batch_size的一维NDArray,执行l.backward()等价执行l.sum().backward()。

for epoch in range(num_epochs):
    #训练模型需要num_epochs个迭代周期
    #在每一个迭代周期，会使用训练数据集中所有样本一次
    #X和y分别是小批量样本的特征和标签
    for X,y in data_iter: 
    	with autograd.record(): #记录与梯度有关的计算, 
    		l = loss (net(X),y) # l是有关小批量X和y的损失 
    	l.backward() #小批量的损失对模型参数求梯度
    	trainer.step(batch_size)
    l = loss(net(features),labels)
   	print ('epoch %d,loss:%f'%(epoch,l.mean().asnumpy()))
	#先对小批量样本进行迭代和算法的优化，最后再对整体求平方损失。
[out]:
epoch 1,loss:0.040611
epoch 2,loss:0.000105
epoch 3,loss:0.000000

dense = net[0] #表示输入层
true_w,dense.weight.data()

([2, -3.4], 
 [[ 1.9999999 -3.3999996]]
 <NDArray 1x2 @cpu(0)>)

---

softmax回归

对于输出为连续值的情况，使用上述模型是可以的，但对于离散值预测问题，可以使用softmax回归在内的分类模型，softmax回归的输出单元从一个变成多个，且引入softmax运算使输出更适合离散值

分类问题

输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像的4像素记为x₁，x₂，x₃，x₄。
假设训练数据集中图像的真实标签位狗、猫或鸡，对应离散值y₁，y₂，y₃

softmax函数

在数学，尤其是概率论和相关领域中，Softmax函数，或称归一化指数函数，是逻辑函数的一种推广。
Softmax函数实际上是有限项离散概率分布的梯度对数归一化。

softmax回归模型

softmax回归和线性回归一样将输出特征与权重做线性叠加，这里假设输入为4像素（宽和高均为2的图像），分别记为x₁,x₂,x₃,x₄,输出有3个，表示真实标签狗、猫或鸡，记为y₁,y₂,y₃，因此权重包含12个标量（带下标的w），偏差有3个标量（带下标的b），有如下公式：

o1=x₁w₁₁+x₂w₂₁+x₃w₃₁+x₄w₄₁+b₁,

o2=x₁w₁₂+x₂w₂₂+x₃w₃₂+x₄w₄₂+b₂,

o3=x₁w₁₃+x₂w₂₃+x₃w₃₃+x₄w₄₃+b₃.

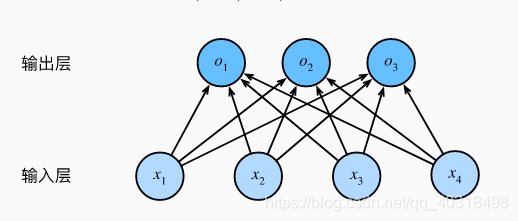
softmax运算

既然分类问题需要得到离散的预测输出，我们不能简单的按数字大小来作为预测输出，因此我们因此了softmax函数，softmax的输出为正且和为1，它是一个合法的概率分布。所以我们按概率大小来作为预测输出。softmax运算不改变预测类别的输出。

单样本分类的矢量计算表达式

softmax回归的权重和偏差为：

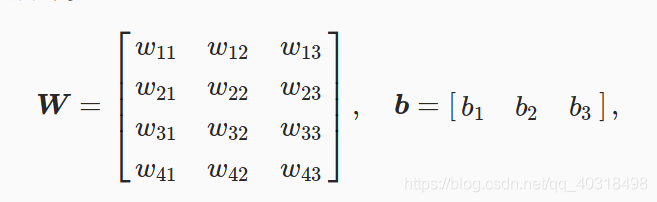
对于w的命名，前面是输入层第几个参数，后面是下一层输出的第几个参数。

---

交叉熵损失函数

• 注意，交叉熵刻画的是两个概率分布之间的距离，或可以说它刻画的是通过概率分布q来表达概率分布p的困难程度，p代表正确答案，q代表的是预测值，交叉熵越小，两个概率的分布约接近。
• 通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了

---

图像分类数据集(Fashion-MNIST)

图像分类数据集中最常用的是手写数字识别数据集MNIST，但大部分模型在MNIST上的分类精度都超过95%。为了更直观观察算法差距，使用图像内容更复杂的Fashion-MNIST

获取数据集

mnist_train = gdata.vision.FashionMNIST(train=True)
mnist_test = gdata.vision.FashionMNIST(train=False)
# 训练集和测试集中的每个类别的图像数分别为6000和1000,10个类别，总数60000和10000
feature,label = mnist_train[1]  # 访问图像和标签，标签就是属于的类别，这是是0-9
#feature对应高和宽均为28像素的图像，相当于28*28矩阵
#每个像素的值在0-255之间，最后一维是通道数，灰度图像，通道数是1
#feature.shape = 28*28*1，feature.dtype = numpy.uint8
# 图像的标签使用Numpy的标量表示，32位整数，label = 2

标签转换

def get_fashion_mnist_labels(labels):   #列表
    text_labels = ['t-shift','trouser','pullover','dress','coat','sandal',
                   'shirt','sneaker','bag','ankle boot']
    return [text_labels[int(i)] for i in labels]

显示图像

def show_fashion_mnist(images,labels):
    display.set_matplotlib_formats('svg')
    # _表示忽略，不使用的变量
    _,figs = d2l.plt.subplots(1,len((images)),figsize=(12,12))
    for f,img,lbl in zip(figs,images,labels):   #zip 转换成元组
        f.imshow(img.reshape((28,28)).asnumpy())    # 显示该图像,没有画出
        f.set_title(lbl)        #设置标题
        f.axes.get_xaxis().set_visible(False)  # 不显示x轴坐标
        f.axes.get_yaxis().set_visible(False)   # 不显示y轴坐标
X,y = mnist_train[0:9]      # 取0-9范围
show_fashion_mnist(X,get_fashion_mnist_labels(y))
d2l.plt.show()  #画出图形.

注意：源码没有使用函数d2l.plt.show()，因此是不会显示图像的

运行结果

---

小结

• Fashion-MNIST是一个10类服饰分类数据集
• 我们将高和宽分别为h和w像素的图像的形状记为h*w或(h,w)