单变量线性回归(LinearRegression with One Variable)
1模型表示
以之前的房屋交易问题为例,假使我们回归问题的训练集(Training Set)如下表所示:
||) |
| 房子的大小(feet^2) | 房子的价格(美元 |
|---|---|
| 2014 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| … | … |
我们将要用来描述这个回归问题的标记如下:
m 代表训练集中实例的数量
x 代表特征/输入变量
y 代表目标变量/输出变量
(x, y) 代表训练集中的实例
/xi,yi./x^i,y^i./xi,yi.代表第i个观察实例
ℎ 代表学习算法的解决方案或函数也称为假设(hypothesis)
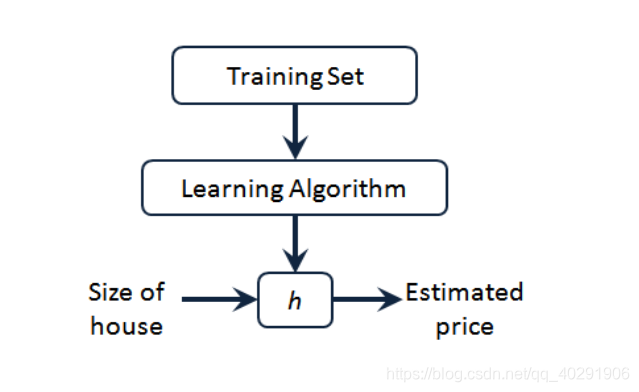
这就是一个监督学习算法的工作方式,我们可以看到这里有我们的训练集里房屋价格我们把它输入给我们的学习算法,学习算法的工作了,然后输出一个函数,通常表示为小写ℎ表示。ℎ代表 hypothesis(假设), ℎ表示一个函数,输入是房屋尺寸大小,就像你朋友想出售的房屋,因此ℎ根据输入的 x值来得出 y 值, y 值对应房子的价格 因此, ℎ 是一个从x到y 的函数映射。这里的h,就可以用一个简单的线性方程表示:
hθ(x)=θ0+θ1xh_\theta (x)=\theta_0+\theta_1xhθ(x)=θ0+θ1x
因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题
2.代价函数
在1中介绍了线性模型,我们现在要做的是为我们的模型选择合适的参数(parameters)θ0\theta_0θ0和θ1\theta_1θ1,在房价问题这个例子中便是直线的斜率和在� 轴上的截距。我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的值与训练集中实际值之间的差距(下图中蓝线所指)就是建模误差(modeling error).
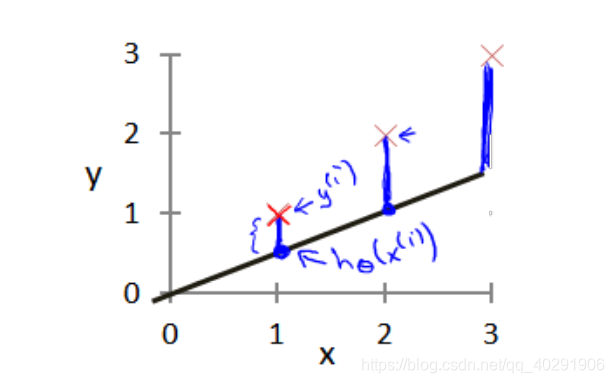
根据算法出
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价
函数 J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{i})-y^{i})^2J(θ0,θ1)=2m1∑i=1m(hθ(xi)−yi)2最小。
为了更好的理解 代价函数我们可以假设θ0=0\theta_0=0θ0=0那么hθ(x)h_\theta(x)hθ(x)的图像为
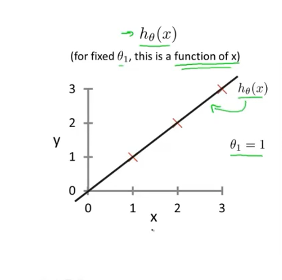
经过计算J(θ1)J(\theta_1)J(θ1)得出一维图像
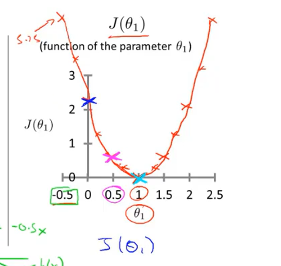
那么图中的最低点为最优解
如果θ0\theta_0θ0不为0的话将此函数映射到三维曲线图中可以得到:
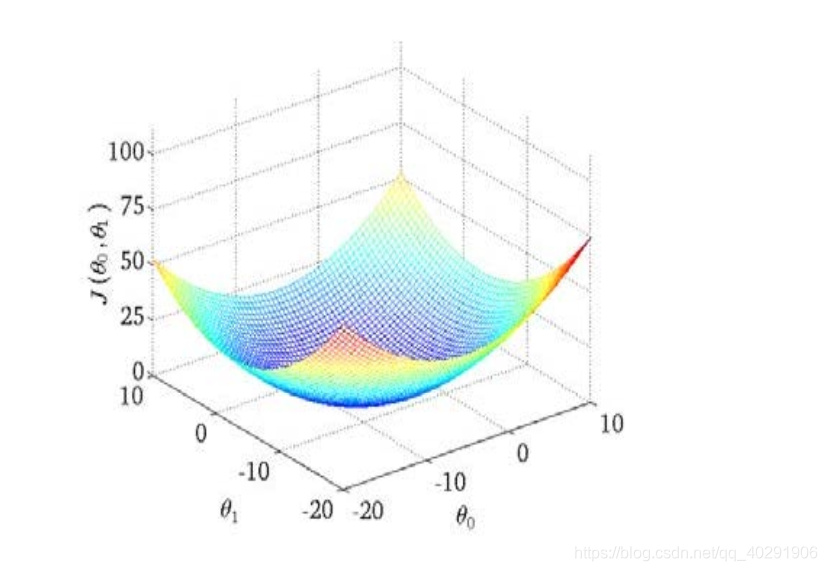
很明显的看出三维图中存在一个点使得J(θ0,θ1)J(\theta_0,\theta_1)J(θ0,θ1)最小;
代价函数也被称作平方误差函数对于大多数问题,特别是回归问题,都是一个合理的选择。还有其他的代价函数也能很好地发挥作用,但是平方误差代价函数可能是解决回归问题最常用的手段了。








 博客围绕单变量线性回归展开,先以房屋交易问题为例介绍模型表示,明确相关标记含义,指出单变量线性回归问题可由简单线性方程表示。接着阐述代价函数,说明要为模型选合适参数使建模误差平方和最小,平方误差代价函数是解决回归问题常用手段。
博客围绕单变量线性回归展开,先以房屋交易问题为例介绍模型表示,明确相关标记含义,指出单变量线性回归问题可由简单线性方程表示。接着阐述代价函数,说明要为模型选合适参数使建模误差平方和最小,平方误差代价函数是解决回归问题常用手段。
















 2723
2723

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








