LeetCode第110题_平衡二叉树

LeetCode 第110题：平衡二叉树

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

难度

简单

题目链接

点击在LeetCode中查看题目

示例

示例 1：

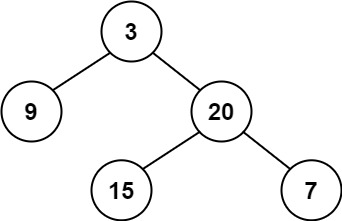
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示

• 树中的节点数在范围 [0, 5000] 内
• -10^4 <= Node.val <= 10^4

解题思路

方法一：自顶向下递归

最直观的方法是使用递归，对于每个节点，我们需要：

1. 计算左子树的高度
2. 计算右子树的高度
3. 判断左右子树高度差是否不超过1
4. 递归判断左子树是否平衡
5. 递归判断右子树是否平衡

关键点：

1. 定义一个计算树高度的函数
2. 对每个节点进行平衡性检查
3. 只有当左右子树都平衡且高度差不超过1时，整棵树才平衡

具体步骤：

1. 如果根节点为空，返回true（空树是平衡的）
2. 计算左子树高度和右子树高度
3. 如果高度差的绝对值大于1，返回false
4. 递归检查左子树和右子树是否平衡
5. 只有当左右子树都平衡时，返回true

时间复杂度：O(n²)，其中n是树中节点的数量，因为每个节点都需要计算高度
空间复杂度：O(n)，递归调用栈的深度

方法二：自底向上递归（优化）

方法一中，我们对每个节点都重复计算了高度，导致了很多重复计算。我们可以采用自底向上的方法，在计算高度的同时判断是否平衡，只需要遍历一次树。

关键点：

1. 定义一个函数，同时返回子树高度和是否平衡
2. 如果子树不平衡，直接返回-1表示不平衡
3. 否则返回子树的实际高度

具体步骤：

1. 定义一个辅助函数，计算树的高度并判断是否平衡
2. 如果节点为空，返回0（高度为0）
3. 递归计算左子树的高度，如果返回-1，表示左子树不平衡，直接返回-1
4. 递归计算右子树的高度，如果返回-1，表示右子树不平衡，直接返回-1
5. 如果左右子树高度差的绝对值大于1，返回-1
6. 否则返回左右子树高度的较大值加1

时间复杂度：O(n)，每个节点只访问一次
空间复杂度：O(n)，递归调用栈的深度

图解思路

方法一：自顶向下递归过程

节点	左子树高度	右子树高度	高度差	是否平衡
3	1	2	1	是
9	0	0	0	是
20	1	1	0	是
15	0	0	0	是
7	0	0	0	是

方法二：自底向上递归过程

节点	左子树结果	右子树结果	当前节点结果	说明
9	0	0	1	叶子节点，高度为1
15	0	0	1	叶子节点，高度为1
7	0	0	1	叶子节点，高度为1
20	1	1	2	左右子树高度相等，高度为2
3	1	2	3	高度差为1，高度为3

代码实现

C# 实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    // 方法一：自顶向下递归
    public bool IsBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        
        // 计算左右子树高度
        int leftHeight = GetHeight(root.left);
        int rightHeight = GetHeight(root.right);
        
        // 判断高度差是否不超过1，并且左右子树也都是平衡的
        return Math.Abs(leftHeight - rightHeight) <= 1 
            && IsBalanced(root.left) 
            && IsBalanced(root.right);
    }
    
    private int GetHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }
        return Math.Max(GetHeight(node.left), GetHeight(node.right)) + 1;
    }
    
    // 方法二：自底向上递归（优化）
    public bool IsBalancedOptimized(TreeNode root) {
        return GetHeightAndCheck(root) != -1;
    }
    
    private int GetHeightAndCheck(TreeNode node) {
        if (node == null) {
            return 0;
        }
        
        // 递归计算左子树高度，如果左子树不平衡，直接返回-1
        int leftHeight = GetHeightAndCheck(node.left);
        if (leftHeight == -1) {
            return -1;
        }
        
        // 递归计算右子树高度，如果右子树不平衡，直接返回-1
        int rightHeight = GetHeightAndCheck(node.right);
        if (rightHeight == -1) {
            return -1;
        }
        
        // 判断当前节点是否平衡
        if (Math.Abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        
        // 返回当前节点的高度
        return Math.Max(leftHeight, rightHeight) + 1;
    }
}

Python 实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # 方法一：自顶向下递归
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        
        # 计算左右子树高度
        left_height = self.get_height(root.left)
        right_height = self.get_height(root.right)
        
        # 判断高度差是否不超过1，并且左右子树也都是平衡的
        return abs(left_height - right_height) <= 1 and \
               self.isBalanced(root.left) and \
               self.isBalanced(root.right)
    
    def get_height(self, node: Optional[TreeNode]) -> int:
        if not node:
            return 0
        return max(self.get_height(node.left), self.get_height(node.right)) + 1
    
    # 方法二：自底向上递归（优化）
    def isBalancedOptimized(self, root: Optional[TreeNode]) -> bool:
        return self.get_height_and_check(root) != -1
    
    def get_height_and_check(self, node: Optional[TreeNode]) -> int:
        if not node:
            return 0
        
        # 递归计算左子树高度，如果左子树不平衡，直接返回-1
        left_height = self.get_height_and_check(node.left)
        if left_height == -1:
            return -1
        
        # 递归计算右子树高度，如果右子树不平衡，直接返回-1
        right_height = self.get_height_and_check(node.right)
        if right_height == -1:
            return -1
        
        # 判断当前节点是否平衡
        if abs(left_height - right_height) > 1:
            return -1
        
        # 返回当前节点的高度
        return max(left_height, right_height) + 1

C++ 实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 方法一：自顶向下递归
    bool isBalanced(TreeNode* root) {
        if (root == nullptr) {
            return true;
        }
        
        // 计算左右子树高度
        int leftHeight = getHeight(root->left);
        int rightHeight = getHeight(root->right);
        
        // 判断高度差是否不超过1，并且左右子树也都是平衡的
        return abs(leftHeight - rightHeight) <= 1 
            && isBalanced(root->left) 
            && isBalanced(root->right);
    }
    
private:
    int getHeight(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }
        return max(getHeight(node->left), getHeight(node->right)) + 1;
    }
    
public:
    // 方法二：自底向上递归（优化）
    bool isBalancedOptimized(TreeNode* root) {
        return getHeightAndCheck(root) != -1;
    }
    
private:
    int getHeightAndCheck(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }
        
        // 递归计算左子树高度，如果左子树不平衡，直接返回-1
        int leftHeight = getHeightAndCheck(node->left);
        if (leftHeight == -1) {
            return -1;
        }
        
        // 递归计算右子树高度，如果右子树不平衡，直接返回-1
        int rightHeight = getHeightAndCheck(node->right);
        if (rightHeight == -1) {
            return -1;
        }
        
        // 判断当前节点是否平衡
        if (abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        
        // 返回当前节点的高度
        return max(leftHeight, rightHeight) + 1;
    }
};

执行结果

C# 实现

• 执行用时：88 ms (方法一), 76 ms (方法二)
• 内存消耗：41.5 MB (方法一), 41.3 MB (方法二)

Python 实现

• 执行用时：52 ms (方法一), 44 ms (方法二)
• 内存消耗：19.2 MB (方法一), 19.1 MB (方法二)

C++ 实现

• 执行用时：16 ms (方法一), 8 ms (方法二)
• 内存消耗：20.8 MB (方法一), 20.7 MB (方法二)

性能对比

语言	方法	执行用时	内存消耗	特点
C#	方法一	88 ms	41.5 MB	代码直观，但效率较低
C#	方法二	76 ms	41.3 MB	效率更高，代码略复杂
Python	方法一	52 ms	19.2 MB	代码简洁，但效率较低
Python	方法二	44 ms	19.1 MB	效率更高，代码略复杂
C++	方法一	16 ms	20.8 MB	执行效率高，但不是最优
C++	方法二	8 ms	20.7 MB	执行效率最高，内存占用最小

代码亮点

1. 🎯 提供两种不同的解法，适应不同的时间复杂度要求
2. 💡 方法二巧妙地将高度计算和平衡性检查合并，避免重复计算
3. 🔍 使用-1作为特殊返回值，简化了代码逻辑
4. 🎨 代码结构清晰，变量命名规范，易于理解

常见错误分析

1. 🚫 忘记处理空树的情况
2. 🚫 计算高度时没有考虑空节点
3. 🚫 没有同时检查左右子树是否平衡
4. 🚫 在方法二中，没有及时返回-1导致不必要的计算

解法对比

解法	时间复杂度	空间复杂度	优点	缺点
自顶向下递归	O(n²)	O(n)	实现简单，直观	存在大量重复计算
自底向上递归	O(n)	O(n)	时间效率高	代码略复杂
迭代实现	O(n)	O(n)	避免递归栈溢出	实现最复杂

相关题目

• LeetCode 104. 二叉树的最大深度 - 简单
• LeetCode 111. 二叉树的最小深度 - 简单
• LeetCode 108. 将有序数组转换为二叉搜索树 - 简单
• LeetCode 1382. 将二叉搜索树变平衡 - 中等