NND今天终于把KD树弄懂了，花了劳资两个小时的有效时间

kd树

kd树的作用：
数据量大时快速找到临近的k点
避免每次重新计算距离，算法会把距离信息保存在一棵树里，需要时直接调用

kd树原理：

kd树核心:

1.树的建⽴；

建立kd树的核心原理：⼩于等于就进⼊左⼦树分⽀，⼤于就进⼊右⼦树分 ⽀直到叶⼦结点


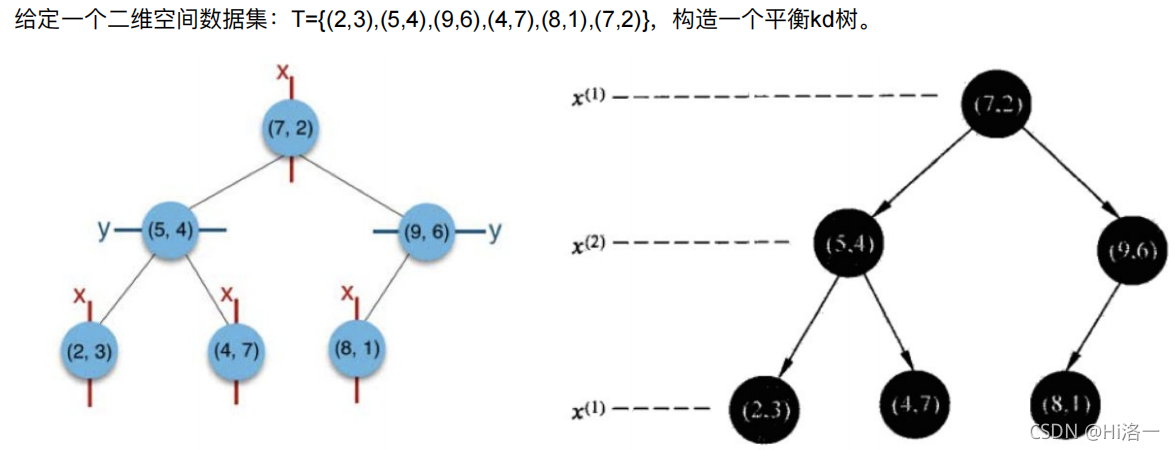
取数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)} x轴按顺序排列选出中位数（x选出来后因为是二维向量坐标所以y也出来了（7,2））
1.在根节点先比较x坐标，比较完后，在下个坐标点比较y坐标
此处的作用是根据二分法的原理不断缩小范围来减少比较次数

最终把各个范围距离缩短绘画出这样的图形：

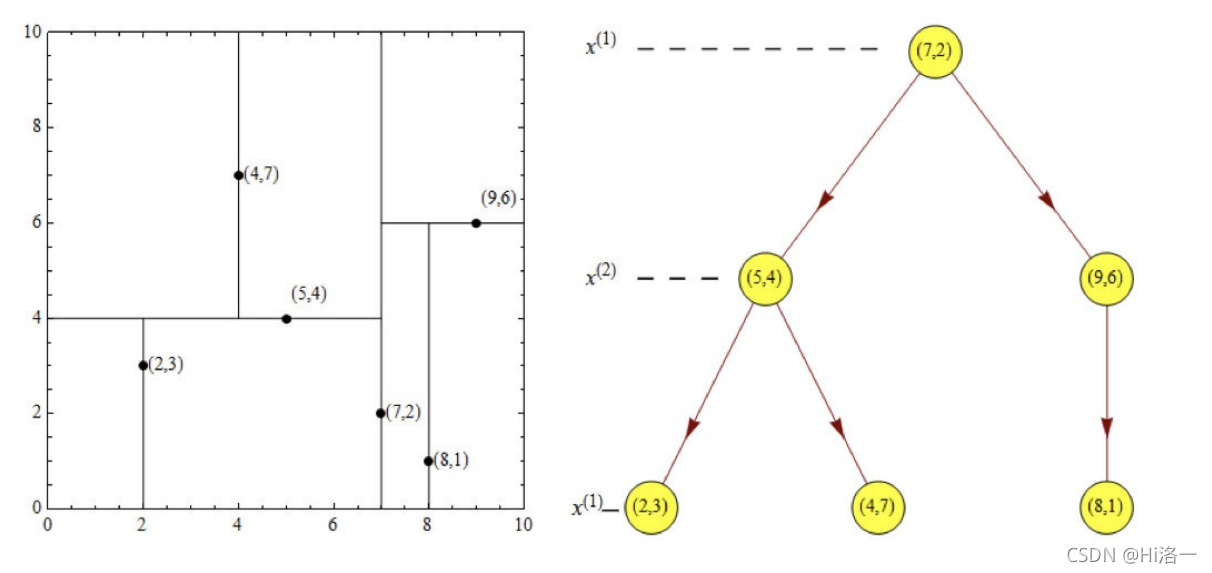
2.最近邻域搜索（Nearest-Neighbor Lookup）

样本集{(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)}

重点来了，重点是运用最临近域搜索找出下面的这两个点，这两个点找出来你就完全弄懂了！

查找点(2.1,3.1)

在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2),(5,4), (2,3)>，从search_path中 取出(2,3)作为当前最佳结点nearest, dist为0.141；
然后回溯⾄(5,4)，以(2.1,3.1)为圆⼼，以dist=0.141为半径画⼀个圆，并不和超平⾯y=4相交，如上图，所以不必跳到结 点(5,4)的右⼦空间去搜索，因为右⼦空间中不可能有更近样本点了。
于是再回溯⾄(7,2)，同理，以(2.1,3.1)为圆⼼，以dist=0.141为半径画⼀个圆并不和超平⾯x=7相交，所以也不⽤跳到结 点(7,2)的右⼦空间去搜索。
⾄此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

查找点(2,4.5)

核心：运用两点之间的距离公式找到最终距离查找点最小的点 与超平面轴对比如果圆半径小于到轴的距离，相当于到了二分法的有用范围的这边，另一边就不用看了

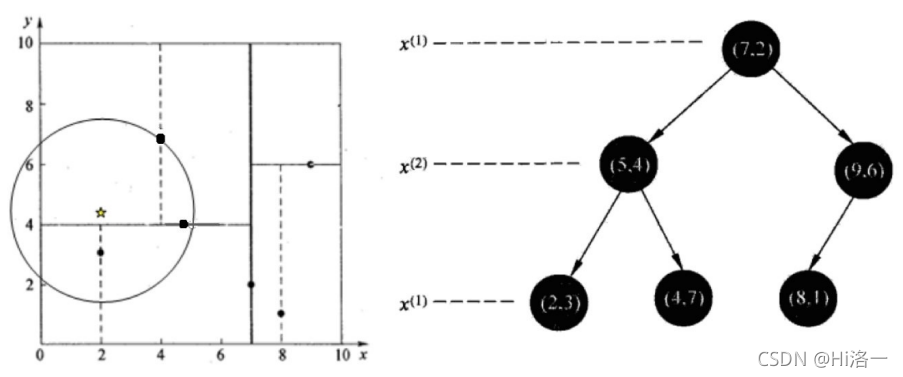
在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)【优先选择在本域搜索】，然后search_path中的结点为<(7,2),(5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；
然后回溯⾄(5,4)，以(2,4.5)为圆⼼，以dist=3.202为半径画⼀个圆与超平⾯y=4相交，所以需要跳到(5,4)的左⼦空间去 搜索。所以要将(2,3)加⼊到search_path中，现在search_path中的结点为<(7,2),(2, 3)>；另外，(5,4)与(2,4.5)的距离为 3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
回溯⾄(2,3)，(2,3)是叶⼦节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)， dist更新为(1.5) 回溯⾄(7,2)，同理，以(2,4.5)为圆⼼，以dist=1.5为半径画⼀个圆并不和超平⾯x=7相交, 所以不⽤跳到结点(7,2)的右⼦ 空间去搜索。
⾄此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

总结：

一. 总结kd树的构建过程
1.构造根节点
2.通过递归的⽅法，不断地对k维空间进⾏切分，⽣成⼦节点
3.重复第⼆步骤，直到⼦区域中没有示例时终⽌ 需要关注细节：a.选择向量的哪⼀维进⾏划分；b.如何划分数据
二. kd树的搜索过程【知道】
1.⼆叉树搜索⽐较待查询节点和分裂节点的分裂维的值，（⼩于等于就进⼊左⼦树分⽀，⼤于就进⼊右⼦树分 ⽀直到叶⼦结点）
2.顺着“搜索路径”找到最近邻的近似点
3.回溯搜索路径，并判断搜索路径上的结点的其他⼦结点空间中是否可能有距离查询点更近的数据点，如果有 可能，则需要跳到其他⼦结点空间中去搜索
4.重复这个过程直到搜索路径为空