论文笔记 Enhancing the Locality and Breaking the MemoryBottleneck of Transformer on Time Series Forecas

最新推荐文章于 2025-06-05 16:53:26 发布

UQI-LIUWJ

最新推荐文章于 2025-06-05 16:53:26 发布

阅读量3.3k

点赞数 4

分类专栏：论文笔记文章标签： transformer 深度学习人工智能

本文链接：https://blog.youkuaiyun.com/qq_40206371/article/details/126369053

版权

论文笔记专栏收录该内容

398 篇文章

订阅专栏

NIPS 2019

1 简介

相比于RNN，Transformer可以更好地建模长时间序列
- RNN 训练起来比较困难（梯度消失/梯度爆炸）
- RNN对于捕捉长期依赖关系比较困难
但是Transformer也有一定的问题：
- 局部性不可感知
- 存储空间瓶颈
  - 传统Transformer的空间和时间复杂度是 $O(n^2)$
  - 这篇论文提出来的LogSparse Transformer 的内存消耗是 $O(N(logN)^2)$

2 背景知识

2.1 问题定义

假设有N个相关的时间序列 $\{Z_{I,1:t_0}\}^N_{t=1}$ ，其中每个 $z_{i,1:t_0}$ 是时间序列i $[z_{i,1},\cdots,z_{i,t_0}]$
任务是希望预测之后所有时间序列的τ时间步 $\{z_{i,{t_0+1}:{t_0+\tau}}\}$
与此同时，令 $\{x_{i,1:t_{0+\tau}}\}^N_{i=1}$ 表示和时间序列相关联的向量（比如一周的哪一天，一天的哪个小时等）
计划是通过X和Z预测未来时间步的z

对于等式右侧各个条件概率，问题可以简化为： $p(z_t|z_{1:t-1},x_{i,1:t};\Phi )$
方便起见，我们把z和x合并成一个增广矩阵Y

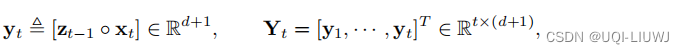
2.2 Transformer

机器学习笔记：Transformer_UQI-LIUWJ的博客-优快云博客

预测时间序列的时候，我们是不能看到未来时间序列的信息的，所以这里的attention矩阵，上三角矩阵全是-∞

3 方法

3.1 提升Transformer可以看到的局部性

传统的Transformer中，我们是对每个点单独进行Q,K,V的投影计算的。
这导致的一个问题是，比如图(a)中的两个红点，他们尽管在时间序列上的特征不同（一个是陡增一个是缓趋势），但是由于绝对数值一样，所以算出来的两个attention是很接近的
而(c）中框起来的两块区域，他们的局部特征是很类似的，但是由于他们的绝对数值不一样，所以算出来的两个attention不大（但理论上应该是比较大的）

为了让Transformer的Q,K可以看到一定时间序列的局部特征，这里引入了卷积自注意力。

这里使用stride为1，kernel大小为k的因果卷积来计算Q和K。通过因果卷积，Q和K可以更好地知晓当前时刻的局部时间序列信息
传统Transformer可以看成这种情况的特例，即k=1的情况

3.2 解决Transformer 内存瓶颈的问题

3.2.1 局部attention实验

作者首先做了实验，可视化了传统Transformer各层学到的attention究竟来自哪个时刻

可以看到，在第二层的时候，attention可能还来自于很远处的时间片；但是到了第10层的时候，attention基本上就来自于局部的时间片了。

——>所以在进行attention的时候，一定的稀疏性可能不会很显著地影响结果

3.2.2 LogSparse Transformer

于是这篇论文提出了LogSparse Transformer
- 每一层的每一个单元只需要计算O(logL)次内积
- 最多迭代O(logL)层
- ——>所以总的空间复杂度是 $O(L*logL*logL)=O(L(logL)^2)$
记为l时刻的单元从第k层到第k+1层所能看到的其他时间序列单元的集合
- 传统Transformer中 $I_l^k=\{j:j\le l\}$
- 在这里，作者希望 $I_l^k \subset \{j:j\le l\}, |I_l^k| \propto logL$
记表示第k层第l个单元可以看到的所有时间序列单元的集合
- 如果最后一层，每一个l单元的 $S_l^{k}$ 都包含了所有在它前面的时刻单元，那么就是一个有效的全局attention
- 换言之，任取单元l，和一个在l前面的时刻单元j，都有一条路径 $P_{jl}=(j,p_1,p_2,\cdots,l), j \in I^1_{p_1},p_1 \in I^2_{p2}, \cdots, p_{k-1} \in I_l^{k}$
LogSparse 自注意力的设计是， $I^k_l=\{l-2^{\lfloor log_2l \rfloor},l-2^{\lfloor log_2l \rfloor-1},l-2^{\lfloor log_2l \rfloor-2},\cdots,l-2^{0},l\}$