递归与回溯：算法解析及实例-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_40185047/article/details/122813736

递归

程序调用自身的编程技巧称为递归（ recursion）。 

为了描述问题的某一状态，必须用到该状态的上一个状态；而如果要描述上一个状态，又必须用到上一个状态的上一个状态…… 这样用自己来定义自己的方法就是递归。

递归生成斐波那契数列

fibonacci(n):       // n 表示求数列中第 n 个位置上的数的值
    if n == 1:        // 设置结束递归的限制条件
        return 1
    if n == 2:        // 设置结束递归的限制条件
        return 1
    return fibonacci(n-1) + fibonacci(n-2)    // F(n) = F(n-1) + F(n-2)

递归只需要一味的重复你写的函数，在上次调用为起点，反复调用自身来达到计算的目的。在大规模状态是灵活的数据中，它得出的数据不一定是正确的。

回溯

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步，还原状态，重新选择，这种走不通就退回再走就是回溯法。

使用回溯法遍历图中节点

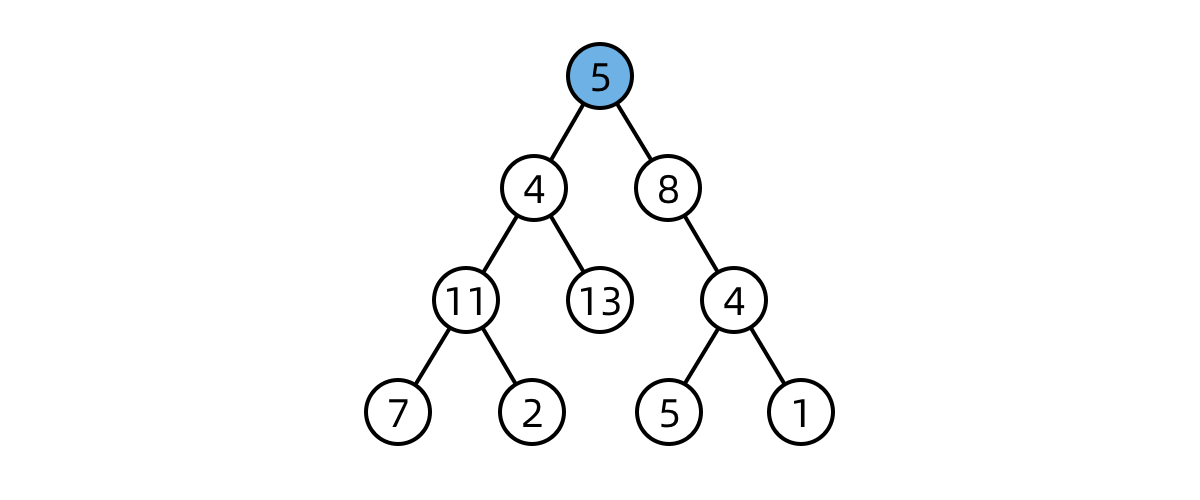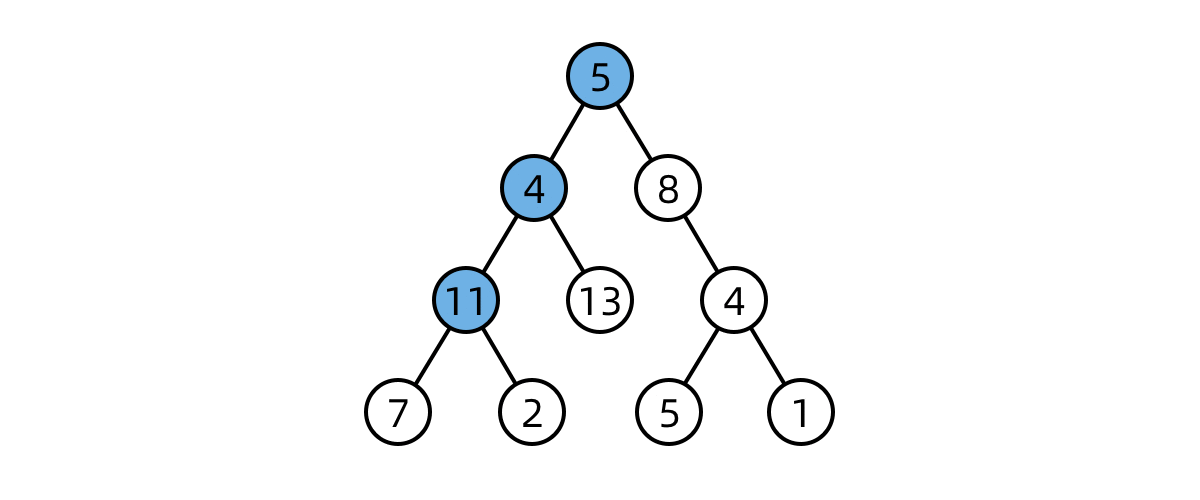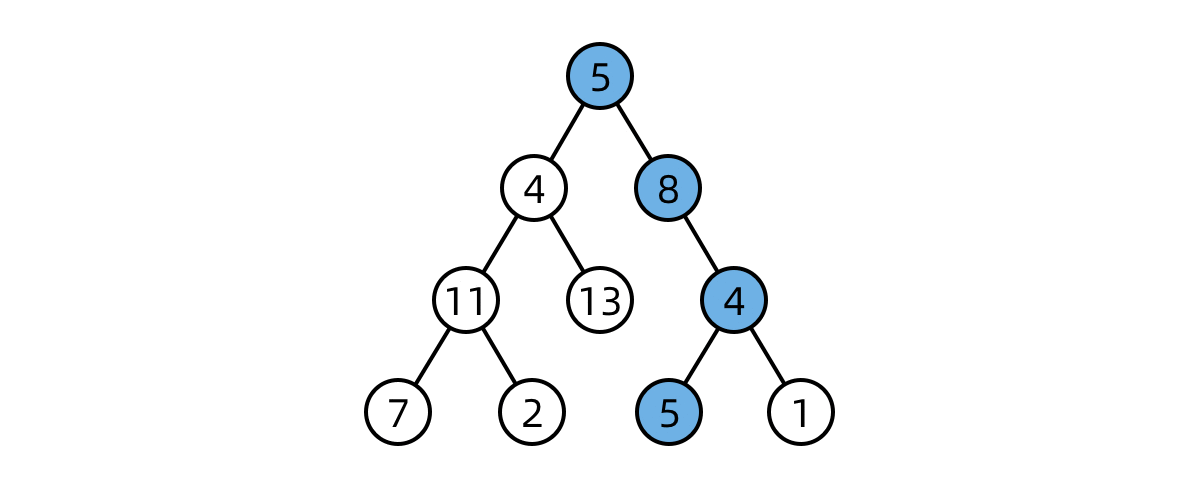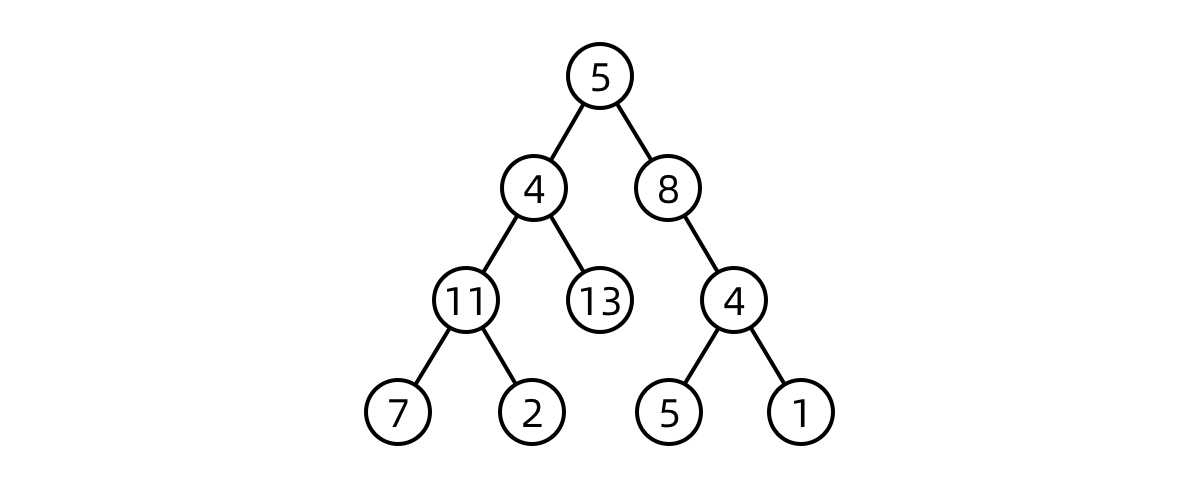
图像大致意思：当面临多个方向选择时，优先选择左边。当执行完毕后回溯，走向另一个选择。

递归与回溯的区别

我们在路上走着，前面是一个多岔路口，因为我们并不知道应该走哪条路，所以我们需要尝试。

我们选择了一个方向，后来发现又有一个多岔路口，这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上，再做一次尝试，即在函数内部再调用一次函数，这就是递归的过程。

这样重复了若干次之后，发现这次选择的这条路走不通，这时候我们知道我们上一个路口选错了，所以我们要回到上一个路口，把脚印抹干净，重新选择其他路，这就是回溯的思想。

最经典的全排列（回溯思想）

package 排列数;
 
import java.util.ArrayList;
 
import java.util.Scanner;
 
public class Main {
	static int n;
	static ArrayList<Integer> list = new ArrayList<Integer>();
	static int[] arr = {0,1,2,3,4,5,6,7,8,9};
	static boolean[] check = new boolean[arr.length];
	static int count = 0;
public static void main(String[] args) {
	Scanner sr = new Scanner(System.in);
	n = sr.nextInt();
	sr.close();
	//进入递归
	f(0);
}
private static void f(int length) {
	if (length == 10) {
		//System.out.println(list);
		count++;//计数器,第count个全排列
		if (count == n) {
			for (Integer item : list) {
				System.out.print(item);
			}
			System.exit(0);//结束程序
		}
	}else {
		for (int i = 0; i < 10; i++) {
			if (!check[i]) {
                //状态标记
				check[i] = true;
				list.add(arr[i]);
                //进入递归
				f(length+1);
                //状态还原
				check[i]= false;
				list.remove(list.size()-1);
			}
		}
	}
}
}

记住还原状态就是回溯啦！