常用排序算法

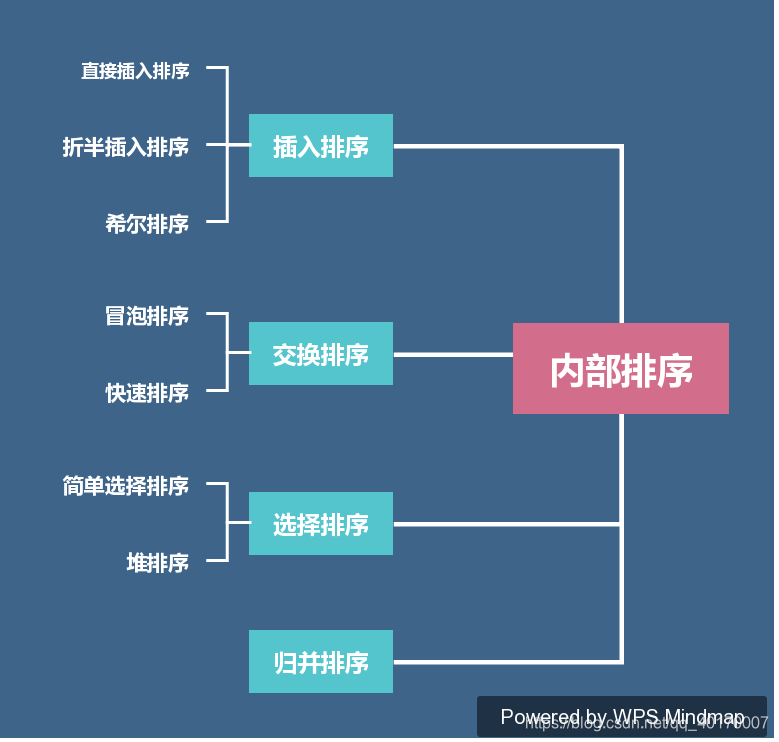
常用的七大排序算法如下：

1、直接插入排序

void insert_Sort(int *a,int n){
	for(int i=0;i<n;i++){
	//key:a[i]
		int temp=a[i];//temp在这里相当于哨兵的作用
		int j;
		for(j=i-1;temp<a[j];j--)
       {//从后向前寻找插入的位置，边找边后移
		a[j+1]=a[j];
       }
        a[j+1]=temp;
	}
}

时间复杂度：O（n^2）当数据基本有序时，可达到O（n）

空间复杂度：O（1）

属于稳定的排序算法

 2、折半插入排序

直接插入算法中，总是边比较边移动元素，而折半插入排序则是将比较和移动的操作分离出来，即先折半查找出元素的待插入位置，然后再统一的移动待插入位置后的所有元素，

void insert_Sort2(int a[],int n){
    int i,j,low,high,mid,temp;
	for(i=0;i<n;i++)
	{temp=a[i];//暂存，哨兵
	    low=0;
		high=i-1;
		while(low<=high){//折半查找元素的位置
		 mid=(low+high)/2;
		 if(a[mid]>a[tmp])
			 high=mid-1;
		 else
			 low=mid+1;
		}
	for(j=i-1;j>=high+1;j--)
		a[j+1]=a[j];
	a[high+1]=temp;}
}      

虽然减少了比较的次数，但时间复杂度仍与直接插入排序相同

3、希尔排序

希尔排序是一种插入排序算法，又称为“缩小增量的排序”，思想是将待排序列分割成若干的字序列，对这些子序列分别进行直接插入排序，当表中元素已经基本有序时，再对全体进行直接插入排序。

（1）当序列已经基本有序时，效率较高

（2）当元素个数较少时，效率较高

步长的设置为：d1=2,d{i+1}=d{i}/2(向下取整)

void ShellSort(int a[],int size)
{
   int step,i,j;//控制步长的变量
   for(step=size/2;step>=1;step=step/2){//控制步长，每次step/2
      for(i=step;i<size;i++)//从第一组的第二个元素开始，依次向后，
		  //比较其与同组的前一个元素的大小，开始进行直接插入排序
	  {
		  if(a[i]<a[i-step]){
			int temp=a[i];//temp为哨兵
			for(j=i-step;temp<a[j];j=j-step){//同组的元素如果前一个元素大于后面的元素，则后移，
			   a[j+step]=a[j];
			}
			a[j+step]=temp;
		  }
	  }
   }
}

时间复杂度：约为O(n^1.3),最坏情况下为O(n^2)

空间复杂度：O(1)

4、冒泡排序

void BubbleSort(int a[],int n){
	if(a==NULL||n==0)
		return;
	for(int i=0;i<n;i++){
		for(int j=n-1;j>i;j--){
		  if(a[j]<a[j-1])
			  swap(a[j],a[j+1]);
		}
	}

}

时间复杂度：O(N^2)  当序列基本有序时，为O（n）

空间复杂度：O（1）

5、快速排序

快速排序的基本思想是基于分治法的，在待排序的元素列表中，取第一个元素作为基准，通过一趟排序可以将该序列划分为两部分，基准前面的元素比他小，基准后的元素比他大，这称为一趟快速排序

int Partition(int arr[],int low,int high){//划分算法
     int pivot=arr[low];//设置第一个元素为枢轴值
	 while(low<high){
		 while(low<high&&arr[high]>=pivot){//从后向前，将比枢轴小的元素移到左边
		  high--;
		 }
		 arr[low]=arr[high];
		 while(low<high&&arr[low]<=pivot){//从前向后，将比枢轴大的元素移到右边
		  low++;
		 }
		 arr[high]=arr[low];
	 }
	 arr[low]=pivot;
	 return low;
}
void QuickSort(int arr[],int low,int high){//利用递归进行快速排序
	if(low<high){
	int pos=Partition(arr,low,high);
	QuickSort(arr,low,pos-1);
	QuickSort(arr,pos+1,high);
	}
}

时间复杂度：O（nlog2n）    最坏情况下数列基本有序时，为O（n^2）

空间复杂度：O(log2n) 

6、简单选择排序

排序思想：

每一趟（例如第i趟排序）在后面的待排序元素中选取关键字最小的元素，作为有序序列的第i个元素，直到第n-1趟做完，待排序元素只剩下一个时。

void SelectSort(int arr[],int n){
	for(int i=0;i<n;i++){
	  int min=i;//用于定位最小元素的下标
	   for(int j=i+1; j<n;j++){//从第i各元素开始找到最小的元素，把下标赋值给min
	     if(arr[j]<arr[min])
			 min=j;
		 
	   }
	   if(min!=i) swap(arr[i],arr[min]);
}

时间复杂度：O（n^2）

空间复杂度：O（1） 

7、归并排序

采用分治的思想，先对每个子序列进行排序，再合并有序的子序列

#include<stdio.h> 
#include<stdlib.h>
void Merge(int *R,int low,int m,int high)  
{  
    int i=low,j=m+1,k=0;                //置初始值  
    int *p;                        //R1是局部向量  
    p=(int*)malloc((high-low+1)*sizeof(int));  
    if(!p)  
    {  
        return;                         //申请空间失败  
    }  
  
    while(i<=m&&j<=high)                //两子文件非空时取其小者输出到R1[p]上  
    {  
        p[k++]=(R[i]<=R[j])?R[i++]:R[j++];  
    }  
  
    while(i<=m)                         //若第1个子文件非空，则复制剩余记录到R1中  
    {  
        p[k++]=R[i++];  
    }  
    while(j<=high)                      //若第2个子文件非空，则复制剩余记录到R1中  
    {  
        p[k++]=R[j++];  
    }  
  
    for(k=0,i=low;i<=high;)  
    {  
        R[i++]=p[k++];                     //归并完成后将结果复制回R[low..high]  
    }  
}  
  
void MergeSort(int R[],int low,int high)  
{     
    //用分治法对R[low..high]进行二路归并排序  
    int mid;  
    if(low<high)  
    {   //区间长度大于1   
        mid=(low+high)/2;               //分解  
        MergeSort(R,low,mid);           //递归地对R[low..mid]排序  
        MergeSort(R,mid+1,high);        //递归地对R[mid+1..high]排序  
        Merge(R,low,mid,high);          //组合，将两个有序区归并为一个有序区  
    }  
}  
void main()  
{  
    int a[7]={49,38,65,97,76,13,27}; //这里对8个元素进行排序  
    int low=0,high=6;                   //初始化low和high的值  
    int i;
    printf("Before merge sort: ");  
    for(i=low;i<=high;i++)  
    {  
        printf("%d ",a[i]);             //输出测试  
    }  
    printf("\n");  
  
    MergeSort(a,low,high);  
  
    printf("After merge sort:  ");  
    for( i=low;i<=high;i++)  
    {  
        printf("%d ",a[i]);             //输出测试  
    }  
    printf("\n");  
}   

时间复杂度：O（nlog2n）

空间复杂度：O(N)

排序算法中不稳定的排序算法：快速排序，希尔排序，堆排序，简单选择排序

时间复杂度可达到nlog2n的：快速排序，堆排序，归并排序