贪心算法之最优装载问题

14天阅读挑战赛

贪心本质

一个贪心算法总是做出当前最好的选择，也就是说，它期望通过局部最优选择得到全局最优的解决方案。

                                                                                                                —— 《算法导论》

贪心算法在解决问题的策略上“目光短浅”。贪心算法只根据当前信息做出选择，而且一旦做出选择，则不管将来有什么结果，这个选择都不会改变。换言之，贪心算法并不是从整体上做最优考虑，它所做出的选择只是某种意义上的局部最优。在实际应用中，很多问题都可以通过贪心算法得到最优解或最优解的近似解。

对于贪心算法，需要注意以下几个问题。

（1）一旦做出选择，就不可以回溯。

（2）有可能得不到最优解，而是得到最优解的近似解。

（3）选择什么样的贪心策略直接决定算法的好坏。

那么，贪心算法需要遵循什么样的原则呢？

贪亦有道

        “君子爱财，取之有道”，在贪心算法中，“贪亦有道”。在遇到具体问题时，怎么选择要不要用贪心算法呢？如果该问题满足贪心选择和最优子结构这两个性质，就可以使用贪心算法。

   1、贪心选择

        贪心选择是指原问题的整体最优解可以通过一系列局部最优的选择得到：先做出当前最优的选择，将原 问题变为一个相似却规模更小的子问题，而后的每一步都是当前最优的选择。这种选择依赖于已做出的选 择，但不依赖于未做出的选择。

   2、最优子结构

        最优子结构是指原问题的最优解包含子问题的最优解。贪心算法通过一系列的局部最优解（子问题的最 优解）得到全局最优解（原问题的最优解），如果原问题的最优解和子问题的最优解没有关系，则求解子问 题没有任何意义，无法采用贪心算法。例如，对于原问题S={a ，a ，…，a，…，a }，可以在通过贪心选择得到一个当前最优解{a }之后，转换为求解子问题S−{a }，继续求解该子问题，最后对所有子问题的最优解进行合并，即可得到原问题的最优解，如图2-1所示 。

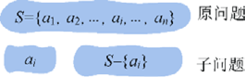
              图2-1 原问题和子问题

最优装载问题

        海盗们截获一艘装满各种各样古董的货船，每一件古董都价值连城，但一旦打碎就会失去其原有的价值。海盗船虽然足够大，但载重量是有限的。海盗船的载重量为W，每件古董的重量为w ，如何才能把尽可能多的古董装上海盗船呢？

问题分析

        问题要求装载的古董尽可能多，在载重量有限的情况下，优先把重量小的古董装进去，装的古董最多。 可以采用重量最小者先装的贪心策略，从局部最优达到全局最优，从而得到最优装载问题的最优解。

完美图解        

        每个古董的重量如表2-1所示，海盗船的载重量W为30，在不打碎古董且不超出载重量的情况下，怎样 才能装入最多的古董呢？

表2-1 古董重量清单

重量w[i]

4

10

7

11

3

5

14

2

（1）贪心策略是每次选择重量最小的古董装入海盗船，因此对表2-1按照古董重量进行非递减排序，排 序结果如表2-2所示。

表2-2 排序后的古董重量清单

重量w[i]

2

3

4

5

7

10

11

14

（2）按照贪心策略，每次选择重量最小的古董装入海盗船（tmp 代表已装入的古董重量，ans代表已装 入的古董数量）。

        ● 选择排序后的第1个古董，装入重量tmp=2，没有超出载重量，ans=1；

        ● 选择排序后的第2个古董，装入重量tmp=2+3=5，没有超出载重量，ans=2；

        ● 选择排序后的第3个古董，装入重量tmp=5+4=9，没有超出载重量，ans=3； 

        ● 选择排序后的第4个古董，装入重量tmp=9+5=14，没有超出载重量，ans=4；

        ● 选择排序后的第5个古董，装入重量tmp=14+7=21，没有超出载重量，ans=5；

        ● 选择排序后的第6个古董，装入重量tmp=21+10=31，超出载重量，算法结束。

        由此可以看出，能够装入海盗船的古董最多为ans=5个。

算法详解

（1）确定合适的数据结构。

用一维数组存储古董的重量：

double[] arras = new double[]{4.0, 10.0, 7.0, 11.0, 3.0, 5.0, 14.0, 2.0};

（2）对古董的重量进行排序。

使用 Arrays.sort() 对古董重量进行降序排序

Arrays.sort(arras);
System.out.println("arras：" + Arrays.toString(arras));
//输出日志：arras：[2.0, 3.0, 4.0, 5.0, 7.0, 10.0, 11.0, 14.0]

（3）按照贪心算法找出最优解

        首先使用变量ans记录装入海盗船的古董数量，并使用变量tmp暂存装入海盗船的古董重量。然后依次检 查每个古董，对tmp加上该古董的重量，如果小于或等于载重量W，则令ans++，否则退出。

private static int solve1(double[] arras) {
    double W = 30;      //海盗船的载重量
    double tmp = 0.0;   //tmp为已装入海盗船的古董重量
    int ans = 0;        //ans为已装入海盗船的古董数量，初始化为0
    for (int i = 0; i < arras.length; i++) {
        tmp += arras[i];
        if (tmp <= W)
            ans++;
        else
            break;
    }
    return ans;
}

//海盗船最多可装的古董数量
int count = solve1(arras);
System.out.println("count:" + count);
//输出日志：count:5

优化拓展

        “算法详解”的第3步“按照贪心策略找出最优解”是否可以优化？实际上，不需要在每次判断是否超出载重量时执行ans++，而是可以初始化ans=n。如果已装入海盗船的古董重量tmp大于或等于载重量 W，则判断是否刚好等于载重量W并令ans=i+1，否则令ans=i并退出。这样就只有最后一次才满足条件，ans 只需要赋值一次即可，或者所有古董都被装入。

private static int solve2(double[] arras) {     //优化算法
    double W = 30;      //海盗船的载重量
    double tmp = 0.0;   //tmp为已装入海盗船的古董重量
    int ans = 0;        //ans为已装入海盗船的古董数量，初始化为0
    for (int i = 0; i < arras.length; i++) {
        tmp += arras[i];
        if (tmp >= W) {
            if (tmp == W)
                ans = i + 1;
            else
                ans = i;
            break;
        }
    }
    return ans;
}