课程7 干涉装置与光场时空相干性、激光 (一) （视频 P21-P24）

干涉装置与光场时空相干性、激光

分波前干涉装置

分波前干涉装置可统归于 “双象系统”。

相干光源的实现----------一分为二，再合二更迭--------目的：消除场点相位差的不稳定性--------------通常可分为两大类：分波前，分振幅。
分波前干涉装置可概括为

分别到达P点的相位差是稳定的，仅取决于几何上的光程差。
交迭区中，场点P的光强取决于相位差δ（p）
光程差 △L（p）=L1（p） - L2（p）
相位差 δ（p）= 2π/λ0 △L（p），稳定，与t无关。

但是，“成像” 不是必要条件，只要实现了分波前再交迭，则有干涉条纹出现在交迭区。不过，一旦归纳为 双象系统，其条纹具体性质便直接作用“杨氏干涉”的结论。
条纹间距
$$\Delta x=\frac{D\lambda }{d}$$
针对具体装置，去确定 等效D，等效d。

在边缘处，直射光程等于反射光程，即表现光程差为零。于是，此处是亮纹或是暗纹，就成为反射时是否发生半波损的实验判据，结果是边缘处出现了暗纹。这就表明在 掠入射时介质界面反射产生相位突变π，这与菲涅尔公式导出的结果一致。但是，这不能证明 光与屏幕无职的相互作用（散射）过程中，光场中的电矢量扮演着主要角色。

对切玻璃、牛顿环示例

条纹的变动

条纹的静态分布；条纹的动态变化-----尝尝联系着 干涉的应用
概述：
光程差 发生变动，条纹发生变动。
三种因素：介质变化、结构发生变化、光源移动
定量关系：若 δ（△L）=N λ0，则此处光强I（p）变化N次。或移动N根条纹（视场印象中）
判断条纹变化的一般方法（或一般原则）：
或固定空间点。看光程差 △L（p）的变化；
或固定光程差值，看空间点的变化------------通常跟踪零级条纹（如果允许的话）----------当情况变动后，零级出现在何处？

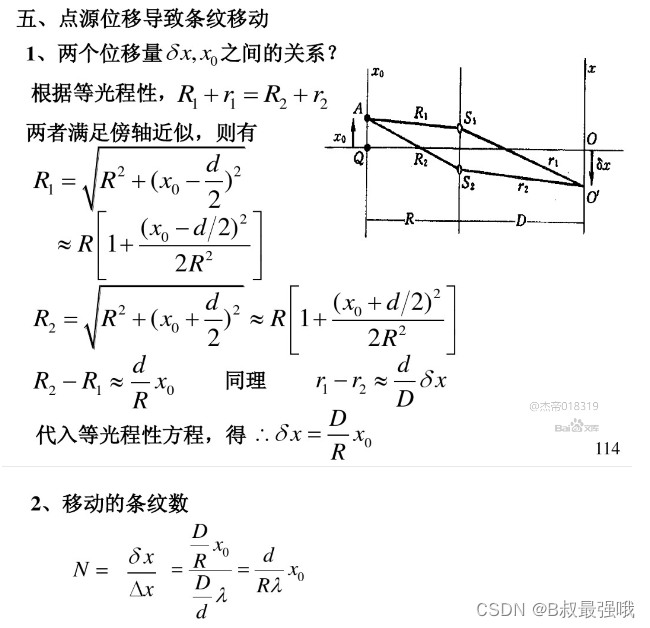
扩展光源对干涉条纹反衬度的影响

概述：
非相干光源，多套条纹非相干叠加，结束；
一般情况，条纹彼此错开，故反衬度下降；
特殊情况下，条纹分布完全一致，维持反衬度不变，且增加条纹亮度。

两个分离点源照射下的部分相干场

反衬度Υ 随着 δx 或 x0的递增而有周期性变化

非相干线光源照明空间中的部分相干场

条纹间距
$$\Delta x=\frac{D\lambda }{d}$$
0极位移
$$\delta x=\frac{D{x}_0}{R}$$
在线光源坐标轴上，取线元 x0 → x0+ △x0，产生干涉强度分布
$$dI(x)\infty (1+cos(2\pi fx+2\pi f_0{x}_0))dx$$
其中，空间频率
$$f=\frac{1}{\Delta x}=\frac{d}{D\lambda },f_0=\frac{d}{R\lambda }$$
改写相移
$$\varphi (x_0)=\frac{2\pi }{\Delta x}\cdot \delta x=2\pi \frac{d}{R\lambda }{x}_0=2\pi f_0{x}_0$$
于是，引入比例常数B，设光源为均匀发光体，则有
$$I(x)={\int }_{\frac{-b}{2}}^{\frac{b}{2}}dI(x)={\int }_{\frac{-b}{2}}^{\frac{b}{2}}B(1+cos(2\pi fx+2\pi f_0{x}_0))d{x}_0$$
积分结束，第一项 Bb = I0 (直流部分)
第二项 B (sinxf0b/πf0) cos2πfx （交变成分）
即
$$I(x)=I_0(1+\frac{sin\pi f_{0}b}{\pi f_{0}b}cos2\pi fx)$$
可见，反衬度
$$\gamma =|\frac{sin\pi f_{0}b}{\pi f_{0}b}|$$

即可知
光源受限宽度 b0 = Rλ/d，当d已知时；
双孔受限间隔 d0 = Rλ/b , 当b给定时。

值得注意的是：
(1) 当b0 成立时，此时线光源的两端点A与B，有两套条纹，彼此错开 N = d/Rλ b0 = 1条，而整体反衬度 γ = 0；
(2) 当b0/2 成立时，此时两套条纹彼此错开，N=0.5条，整体 γ = 0.64.

这些结论可有一个直观图像予以说明。由此引出一个判据（估算）: 用非相干扩展光源，当其边缘点源的光程差之差为 一个波长 λ0时，则考察区域中的γ = 0---------------以此估算极限值。

光场的空间相干性

两个点---------两个次波源(S1、S2) 相干性
S1 点的总扰动
$${\text{U}}_1(t)=(U_A+...+U_O+....+U_B)=\Sigma U_i(t)$$
S2点的总扰动
$${\text{U}}_1(t)=(U_A^{\prime }+...+U_O^{\prime }+....+U_B^{\prime })=\Sigma U_i^{\prime }(t)$$
可见，其中含 完全相干成分 与完全非相干成分，总效果，既非完全相干，又非完全不相干，而是 部分相干，虽然光源是完全非相干的。
相干程度可由双孔干涉实验中的观察屏上 光强分布的反衬度γ值，作为 S1、S2相干度的一种量度。

反映光场空间相干性的反比律公式

引用前面公式，当光源线度b给定，则双孔的极限宽度 d0 = Rλ/b 。
引入角量 △θ0 = d0/R 极限角范围，相干孔径角，
于是
$$b\Delta {\theta }_0\approx \lambda$$
其意义是
(1) 实际双孔的张角 △θ = △θ0，则γ ≈0;△θ < △θ0，则γ >0，部分相干。
(2) 光源线度 b越小，则 △θ0越大；
(3) 由反比律面规划了一个角范围，（S1、S2）处于 △θ0之外，则γ≈0，它俩几乎不相干；（S1、S2）处于 △θ0之内，则γ>0，它俩部分相干；（S1、S2）处于 △θ0 内部越深，则γ越高，相干性越好。

相干面积

由 b· △θ0 ≈ λ ，得 △θ0 ≈ λ/b
距离R 远处的面积（相干面积）
$$\Delta S_0=\frac{\pi }{4}(R\cdot \Delta {\theta }_0{)}^2=(\frac{R\lambda }{b}{)}^2$$
空间相干性反比律公式中的系数
$$b\Delta {\theta }_0=N\lambda$$
针对不同光源 N不一致，线光源 N=1；环形光源 N=0.78；圆盘光源 N=1.22（1节贝塞尔函数确认）
有意思的是 系数的平均值 1/2（0.78+1.22） = 1

利用γ值的变化(下降)，可以精测遥远星体的角径-------化"消极"为"积极"
当d接近d0，γ由1下降至0(干涉条纹消失)，于是 △θ’= λ/d0 d0取1m时，△θ’=5.5*10^-7 rad
这只是一个设想，技术上的实现有问题
（1）可调范围在m量级的双孔，在实验上有诸多分辨（眼睛无法分辨条纹间距）
迈克尔孙星体干涉仪解决了这个矛盾。

评论
(1) 它巧妙地解决了测角高精度与条纹宽间隔之间的矛盾。 短 d → △x = fλ/d, d mm; 长基线 h → △θ’ =λ/h0 ， h0 10³mm；
(2) 在光源与双孔位置不变的条件下，它通过镜面的移动面改变场点(S1、S2)的相关程度，并予以探测。史无前例，这使它成为现代光学相关实验的先导。 虽然这里设计的是 相位型干涉仪中的空间相干性的概念，那里设计的是强度干涉仪。

薄膜干涉

薄膜干涉定域问题
(1) 点光源照明时干涉区---------广延性
(2) 扩展光源照明时干涉区------局限性

通常关注两处干涉场
(1) 表面的----------------------------------------------等厚干涉条纹
(2) 膜厚均匀时远处的干涉场----------------------等倾干涉条纹

因为理论分析简单，实际应用广泛。

等厚条纹
1、理论说明-------------表面条纹的等厚性
2、表面条纹偏离等厚线情形
大倾角时
厚膜层时
薄膜的第一种意义
3、扩展光源将降低表面条纹的反衬度 ------------薄膜的第二种意义

光程差近似公式
$$\Delta L_0(P)=2n{h}_{p}cos{i}_p$$
i p内折射角，n hp 该处播磨光学原膜越薄，则 △θ越小，从而 △L0§ 上述表达式近似程度。
可见 影响光程差的 ，既有厚度h因素，又有倾角 i 因素。
获得等厚条纹的实验条件
(1) 平行光近乎垂直照明
(2) 球面波傍轴销倾角照明(窄光束)
总之，设法实现 ip≈0 << 1, 有 cos ip =1。
于是
$$\Delta L_0(p)=2n{h}_p$$
等厚条纹的性质
(1) 表面条纹形貌与 播磨几何等厚络一致
(2) 当 2nh = k λ0，有亮纹(或暗纹)
当 2nh = (k+1/2) λ0，有暗纹(或亮纹)
(3) 相邻条纹对应的厚度差 λ/2，或条纹变动1次，对应厚度变化 λ/2

楔形薄膜的等厚条纹

可利用该点进行精密测量(劈尖干涉)，测定平面的平直度，若标准件板某处凹起，则出现乙图；若某处凸起，则出现丙图；

牛顿环及其变动

中心点膜厚h0，出现一连串同心干涉环。
(1) 紧密接触，h0= 0。中心–零级暗斑，则 K级暗环半径
$$r_K=\sqrt{KR\lambda }\propto \sqrt{K}，$$
即，
KaTeX parse error: Expected 'EOF', got '}' at position 27: …r_K^2}[K\lambda}̲
该公式意义在于 通过干涉的办法求出平凸透镜的曲率半径
(2) 常见 h0 ≠ 0 ，中心可亮可暗。有
$$R=\frac{r_{K+m}^2-r_K^2}{m\lambda }=\frac{d_{K+m}^2-d_K^2}{4m\lambda }$$

利用牛顿环在光学冷加工车间判断光学透镜是否合乎要求，当对上方G验规施加压力，若牛顿环扩大如a所示，则待测光学透镜L为中心曲率半径待研磨；若牛顿环收缩如b，则待测光学透镜为边缘待研磨

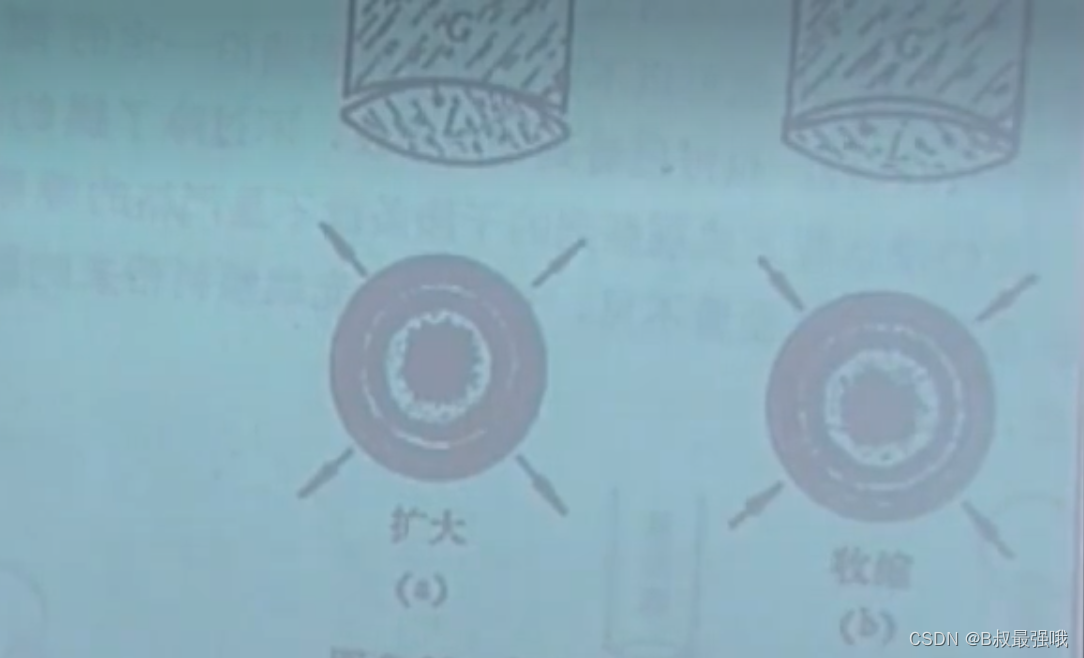
等厚条纹用于精密测量，可用于测量角度、微厚度、相关物理量，精度可达到100nm。

表面条纹偏离等厚线的情况

傍轴小倾角光束 ，则出现的是平直干涉条纹，如左侧图。如光阑打开，照明光束变为大倾角，则干涉条纹变弯，且弯曲方向朝向0点(棱边夹角交点) 如中侧 图。若膜层厚度增加，则弯曲更明显，如图右。
定性说明：
考察条纹上，两点 p p’，要满足等光程差。
$$2n{h}_{p}cos{i}_p=2n{h}_p^{\prime }cos{i}_p^{\prime }$$
因为 ip’ >ip，cos ip’ < cos ip，因此 hp’ >hp，弯曲凸向棱边。

粗略数学描写
h变化-i变化 有确定关系，以维持
$$2nhcosi=con△t$$
全微分 d（2nhcosi） = 0
考虑到
$$\frac{dh}{di}=htani。\propto tani倾角因素；\propto h膜厚因素$$
说明
大倾角或厚膜层 → dh/di越大，条纹弯曲(偏离等厚线)越明显。

薄膜的意义：
(1)薄膜越薄，条纹形貌等厚线的一致性越好，因而精测的准确性越高。

扩展光源照明，表面条纹的反衬度下降，因为 各点源生成的各套条纹，彼此错位；或者说不同电源有着不同的光程差(相对于同一场点P)

数学粗略描述
与接收光瞳对应的光源边缘两点 AB产生的光程差之差
$$\delta (\Delta L)=-2nhsini\delta i$$
令 δ(△L) < λ0，取 δ(△L) = λ0/2，方有 γ>=0.6的干涉场，可供观测。
为此，确定光源的极限角宽 △iM
有
$$-2nhsini\Delta i_M={\lambda }_0，\Delta i_M=\frac{\lambda }{2hsini}\propto \frac{1}{h}$$
可见，膜层越薄，所允许的光源线度越大，这是薄膜干涉的又一种意义。

如上图所示，虽然线光场 A‘B’，眼睛接收光瞳仅仅只接收了AB两点的光场。

薄膜光学，增透膜，增反膜。

低膜-----消反射膜，即增透膜，光程差 △L = △L0 = λ0/2，相干相消
高膜-----消透射膜，即 增反膜，光程差△L = △L0 + λ0/2 = λ0，相干相长

重要意义：
(1) 为了完全消反射，还需满足振幅相等，由
$$n_2=\sqrt{n_1{n}_g}$$
予以保证。
(2) 镀膜是针对某一波长 λ0，不能对所有波长成分进行增透增反；
干涉滤光片-------其透射光有了谱线宽度 λ

激光器内谐振器就镀了多层介质膜高反膜，反射率高达99.99%。

---

参考内容

1、http://www.icourses.cn/sCourse/course_3571.html
2、https://wenku.baidu.com/view/280ca23943323968001c9207.html?fr=aladdin664466&ind=1&aigcsid=39662&qtype=0&lcid=1&queryKey=%E7%8E%B0%E4%BB%A3%E5%85%89%E5%AD%A6%E5%9F%BA%E7%A1%80&wkts=1708349418827&bdQuery=%E7%8E%B0%E4%BB%A3%E5%85%89%E5%AD%A6%E5%9F%BA%E7%A1%80
3、https://baike.baidu.com/item/%E5%8A%88%E5%B0%96%E5%B9%B2%E6%B6%89/4736392?fr=ge_ala
4、https://baike.baidu.com/item/%E7%89%9B%E9%A1%BF%E7%8E%AF/906788?fr=ge_ala