最近公共子序列（LCA，DFS序，RMQ-ST）

 

解题思路

1、建树

2、用 dfs 将树转换为一维数组

3、rmq(st算法) 预处理 查找

 

第1步 vector建树，这步不难理解，看代码可以看懂。 

 

第2步 dfs转换过程

记录规则就是假设在走路，不管走没走过的地方，只要经过就记录。

记录下 dfs 的序列，还有 dfs 过程中每一个点的深度(即辈分)。还需要记录一个在 dfs 中每一个节点首次出现的位置。

例1

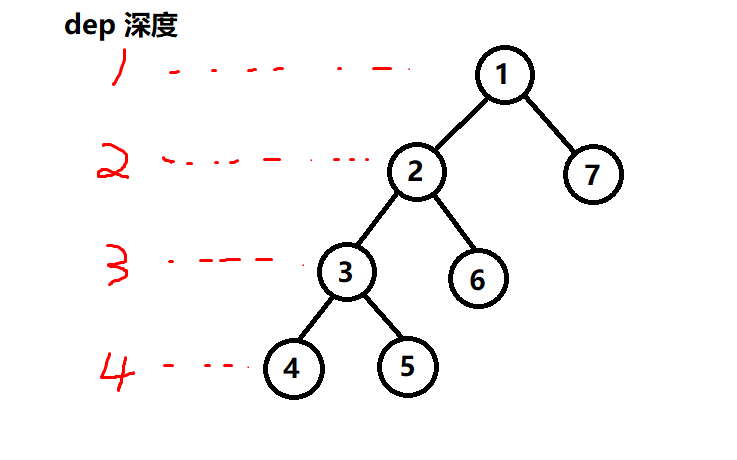
不停地 走左下，回溯，走右下，则：

数组 f 表示经过的序号

与f序号对应的深度(辈分)数组命名为dep

则上图对应的：

f      1 2 3 4 3 5 3 2 6 2 1 7 1

dep 1 2 3 4 3 4 3 2 3 2 1 2 1

 

pos数组表示图中1-7每个点在f数组第一次出现的位置：1 2 3 4 6 9 12

查询两点间的最小公共祖先，即第3步的查找，就是在f数组中两个点第一次出现的位置(即pos)中间的点中找辈分最小的。

比如要找点4和点5的公共祖先，pos[4] = 4(第一次出现的位置为f数组的第四位)，pos[5] = 6(同理)。那么在f数组的第四位和第六位中间只有一个3，所以3就是最小公共祖先，如果中间有很多，则需要找到辈分最小的(即dep最大的)，就是最小公共祖先。

 

第3步 rmq(st算法) 预处理，查找

RMQ (Range Minimum/Maximum Query) 问题是指：对于长度为 n 的数列 A，回答若干询问 RMQ(A,i,j)(i,j<=n)，返回数列 A 中下标在 i,j 里的最小 (大）值，也就是说，RMQ 问题是指求区间最值的问题。

这里我们查找的是i到j区间中深度dep的最大值(即辈分最小)

然后输出深度最大值(即辈分最小)对应的名字即可

以上来自：https://www.cnblogs.com/cuimama/p/9446570.html（为了防止忘了，就赶紧转载过来了 - -） 

模板链接