说到排序,一定离不开这张图
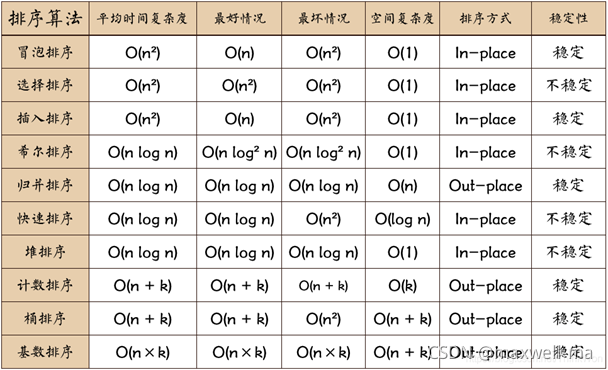
简单排序O(n2)O(n^2)O(n2)
冒泡排序
选择一个最大的数(最小的数)放到最后面的位置,然后选择次大的数(次小的数)放到倒数第二个位置,依次类推,直到所有的数字为止。由冒泡排序衍生出了鸡尾酒排序,听起来很高大上,它是一种双端冒泡,先选一个最小的数,放到第一位,然后选一个最大的数放到最后一位,以此类推。
冒泡排序代码:
//降序排列
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
//交换arr的i和j位置上的值
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
鸡尾酒排序
public static int[] cocktailSort(int[] src){
int len = src.length;
//将最小值排到队尾
for(int i = 0 ; i < len/2 ; i++){
for(int j = i ; j < len-i-1 ; j++){
if(src[j] < src[j+1]){
int temp = src[j];
src[j] = src[j+1];
src[j+1] = temp;
}
System.out.println("交换小"+Arrays.toString(src));
}
//将最大值排到队头
for(int j = len-1-(i+1); j > i ; j--){
if(src[j] > src[j-1]){
int temp = src[j];
src[j] = src[j-1];
src[j-1] = temp;
}
System.out.println("交换大"+Arrays.toString(src));
}
System.out.println("第"+i+"次排序结果:"+Arrays.toString(src));
}
return src;
}
选择排序
每次选择一个数依次放到从左到右的合适位置
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 0 ~ N-1 找到最小值,在哪,放到0位置上
// 1 ~ n-1 找到最小值,在哪,放到1 位置上
// 2 ~ n-1 找到最小值,在哪,放到2 位置上
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
插入排序
将第i个数放到数组左边已经排好序的合适位置
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//0~0有序的
//0~i 想有序
//0~i做到有序
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
O(nlogn)的排序算法
归并排序
顾名思义,将两个有序数组归并成一个有序数组,归并排序算法思想可以应用到求最小和和逆序对等问题上
// 递归方法实现
public static void mergeSort1(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
// 请把arr[L..R]排有序
// l...r N
// T(N) = 2 * T(N / 2) + O(N)
// O(N * logN)
public static void process(int[] arr, int L, int R) {
if (L == R) { // base case
return;
}
int mid = L + ((R - L) >> 1);
process(arr, L, mid);
process(arr, mid + 1, R);
merge(arr, L, mid, R);
}
public static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 要么p1越界了,要么p2越界了
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}
// 非递归方法实现
public static void mergeSort2(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int N = arr.length;
// 步长
int mergeSize = 1;
while (mergeSize < N) { // log N
// 当前左组的,第一个位置
int L = 0;
while (L < N) {
if (mergeSize >= N - L) {
break;
}
int M = L + mergeSize - 1;
int R = M + Math.min(mergeSize, N - M - 1);
merge(arr, L, M, R);
L = R + 1;
}
// 防止溢出
if (mergeSize > N / 2) {
break;
}
mergeSize <<= 1;
}
}
快速排序
随机选择一个数,将数组分成三部分,左边部分小于选择的数,右边部分大于选择的数,中间部分等于选择的数(荷兰国旗问题)
public static void quickSort(int[] arr){
if (arr==null||arr.length<2){
return ;
}
quickSort(arr,0,arr.length-1);
}
//arr[1..r]排好序
public static void quickSort(int[] arr,int L,int R){
if (L<R){
swap(arr,L+(int)(Math.random()*(R-L+1)),R);
int[] p=partition(arr,L,R);
quickSort(arr,L,p[0]-1);
quickSort(arr,p[1]+1,R);
}
}
//这是一个处理arr[1..r]的函数
//默认以arr[r]做划分,arr[r]->p <p ==p >p
//返回等于区域(左边界,右边界),所以返回一个长度为2的数组res,res[0],res[1]
public static int[] partition(int[] arr,int L,int R){
int less=L-1;
int more=R;
while(L<more){
if (arr[L]<arr[R]){
swap(arr,++less,L++);
}else if (arr[L]>arr[R]){
swap(arr,--more,L);
}else{
L++;
}
}
swap(arr,more,R);
return new int[] {less+1,more};
}
//交换arr的i和j位置上的值
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
堆排序
利用堆进行排序的算法,堆有大顶堆和小顶堆
// 堆排序额外空间复杂度O(1)
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// O(N*logN)
// for (int i = 0; i < arr.length; i++) { // O(N)
// heapInsert(arr, i); // O(logN)
// }
// O(N)
for (int i = arr.length - 1; i >= 0; i--) {
heapify(arr, i, arr.length);
}
int heapSize = arr.length;
swap(arr, 0, --heapSize);
// O(N*logN)
while (heapSize > 0) { // O(N)
heapify(arr, 0, heapSize); // O(logN)
swap(arr, 0, --heapSize); // O(1)
}
}
// arr[index]刚来的数,往上
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
// arr[index]位置的数,能否往下移动
public static void heapify(int[] arr, int index, int heapSize) {
int left = index * 2 + 1; // 左孩子的下标
while (left < heapSize) { // 下方还有孩子的时候
// 两个孩子中,谁的值大,把下标给largest
// 1)只有左孩子,left -> largest
// 2) 同时有左孩子和右孩子,右孩子的值<= 左孩子的值,left -> largest
// 3) 同时有左孩子和右孩子并且右孩子的值> 左孩子的值, right -> largest
int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
// 父和较大的孩子之间,谁的值大,把下标给largest
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
希尔排序
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
shellSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description: 希尔排序
*
* @param array
* @return void
* @author JourWon
* @date 2019/7/11 23:34
*/
public static void shellSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int length = array.length;
// temp为临时变量,gap增量默认是长度的一半,每次变为之前的一半,直到最终数组有序
int temp, gap = length / 2;
while (gap > 0) {
for (int i = gap; i < length; i++) {
// 将当前的数与减去增量之后位置的数进行比较,如果大于当前数,将它后移
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
// 将当前数放到空出来的位置
array[preIndex + gap] = temp;
}
gap /= 2;
}
}
非比较排序
计数排序
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
countingSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description: 计数排序
*
* @param array
* @return void
* @author JourWon
* @date 2019/7/11 23:42
*/
public static void countingSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int length = array.length;
int max = array[0];
int min = array[0];
for (int i = 0; i < length; i++) {
if (max < array[i]) {
max = array[i];
}
if (min > array[i]) {
min = array[i];
}
}
// 最大最小元素之间范围[min, max]的长度
int offset = max - min + 1;
// 1. 计算频率,在需要的数组长度上额外加1
int[] count = new int[offset + 1];
for (int i = 0; i < length; i++) {
// 使用加1后的索引,有重复的该位置就自增
count[array[i] - min + 1]++;
}
// 2. 频率 -> 元素的开始索引
for (int i = 0; i < offset; i++) {
count[i + 1] += count[i];
}
// 3. 元素按照开始索引分类,用到一个和待排数组一样大临时数组存放数据
int[] aux = new int[length];
for (int i = 0; i < length; i++) {
// 填充一个数据后,自增,以便相同的数据可以填到下一个空位
aux[count[array[i] - min]++] = array[i];
}
// 4. 数据回写
for (int i = 0; i < length; i++) {
array[i] = aux[i];
}
}
桶排序
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
bucketSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description: 桶排序
*
* @param array
* @return void
* @author JourWon
* @date 2019/7/11 23:43
*/
public static void bucketSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
// 建立桶,个数和待排序数组长度一样
int length = array.length;
LinkedList<Integer>[] bucket = (LinkedList<Integer>[]) new LinkedList[length];
// 待排序数组中的最大值
int maxValue = Arrays.stream(array).max().getAsInt();
// 根据每个元素的值,分配到对应范围的桶中
for (int i = 0; i < array.length; i++) {
int index = toBucketIndex(array[i], maxValue, length);
// 没有桶才建立桶(延时)
if (bucket[index] == null) {
bucket[index] = new LinkedList<>();
}
// 有桶直接使用
bucket[index].add(array[i]);
}
// 对每个非空的桶排序,排序后顺便存入临时的List,则list中已经有序)
List<Integer> temp = new ArrayList<>();
for (int i = 0; i < length; i++) {
if (bucket[i] != null) {
Collections.sort(bucket[i]);
temp.addAll(bucket[i]);
}
}
// 将temp中的数据写入原数组
for (int i = 0; i < length; i++) {
array[i] = temp.get(i);
}
}
/**
* Description: 映射函数,将值转换为应存放到的桶数组的索引
*
* @param value
* @param maxValue
* @param length
* @return int
* @author JourWon
* @date 2019/7/11 23:44
*/
private static int toBucketIndex(int value, int maxValue, int length) {
return (value * length) / (maxValue + 1);
}
基数排序
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
radixSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description: 基数排序
*
* @param array
* @return void
* @author JourWon
* @date 2019/7/11 23:45
*/
public static void radixSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int length = array.length;
// 每位数字范围0~9,基为10
int radix = 10;
int[] aux = new int[length];
int[] count = new int[radix + 1];
// 以关键字来排序的轮数,由位数最多的数字决定,其余位数少的数字在比较高位时,自动用0进行比较
// 将数字转换成字符串,字符串的长度就是数字的位数,字符串最长的那个数字也拥有最多的位数
int x = Arrays.stream(array).map(s -> String.valueOf(s).length()).max().getAsInt();
// 共需要d轮计数排序, 从d = 0开始,说明是从个位开始比较,符合从右到左的顺序
for (int d = 0; d < x; d++) {
// 1. 计算频率,在需要的数组长度上额外加1
for (int i = 0; i < length; i++) {
// 使用加1后的索引,有重复的该位置就自增
count[digitAt(array[i], d) + 1]++;
}
// 2. 频率 -> 元素的开始索引
for (int i = 0; i < radix; i++) {
count[i + 1] += count[i];
}
// 3. 元素按照开始索引分类,用到一个和待排数组一样大临时数组存放数据
for (int i = 0; i < length; i++) {
// 填充一个数据后,自增,以便相同的数据可以填到下一个空位
aux[count[digitAt(array[i], d)]++] = array[i];
}
// 4. 数据回写
for (int i = 0; i < length; i++) {
array[i] = aux[i];
}
// 重置count[],以便下一轮统计使用
for (int i = 0; i < count.length; i++) {
count[i] = 0;
}
}
}
/**
* Description: 根据d,获取某个值的个位、十位、百位等,d = 0取出个位,d = 1取出十位,以此类推。对于不存在的高位,用0补
*
* @param value
* @param d
* @return int
* @author JourWon
* @date 2019/7/11 23:46
*/
private static int digitAt(int value, int d) {
return (value / (int) Math.pow(10, d)) % 10;
}








 本文详细介绍了各种排序算法,包括简单的冒泡排序、选择排序、插入排序,到高效的归并排序、快速排序、堆排序,以及非比较排序如计数排序、桶排序和基数排序。通过代码实现和解析,帮助读者理解每种排序算法的原理和应用场景。
本文详细介绍了各种排序算法,包括简单的冒泡排序、选择排序、插入排序,到高效的归并排序、快速排序、堆排序,以及非比较排序如计数排序、桶排序和基数排序。通过代码实现和解析,帮助读者理解每种排序算法的原理和应用场景。
















 1086
1086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








