插入排序的测试及优化

最新推荐文章于 2025-06-06 13:16:02 发布

ChrisNotMe

最新推荐文章于 2025-06-06 13:16:02 发布

阅读量774

点赞数

CC 4.0 BY-SA版权

分类专栏： JAVA 文章标签： java 排序算法优化

本文链接：https://blog.youkuaiyun.com/qq_40006051/article/details/80618985

JAVA 专栏收录该内容

4 篇文章

订阅专栏

本文探讨了插入排序算法的原理和实现，通过代码示例展示了原始插入排序的执行过程。文章指出，虽然插入排序在某些特定情况下（如近似有序数组）比高级排序算法更快，但其平均时间复杂度为O(n^2)。为了优化，作者提出了一种减少交换和赋值次数的策略，实测显示优化后的算法性能提升了约30%。此外，插入排序在处理大量重复数据时表现出较高的效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

关于O（n^2）的排序算法中，插入排序是不得不提的一种。相比较于冒泡排序，选择排序这些真正的O（n^2）算法，插入算法在一些情况下的性能会比一些高级排序算法如归并排序，快速排序更加高效，而这些情况我们会在下面的一些情况中进行讨论。

首先，既然要写一个插入排序算法，我们第一个要做的自然是理解插入排序的过程是怎么样的。

第一步，给定一个随机产生的数组，从第二个数进行遍历；

第二步，将遍历到的数与前一个数进行比较，如果这个数小于前一个数，则进行交换，再与前面的数进行比较，若小于，则再交换，一直比较到第一个数；

第三步，如果遍历的数大于前一个数，不交换，继续向后遍历；

代码示例：

public class insertionSort {//插入排序

public static  void sort(Comparable[] arr){
    int n = arr.length;
    for(int i=1; i<n; i++){
        for(int j=i; j>0; j--){
            if(arr[j].compareTo(arr[j-1])<0){//如果arr[j]<arr[j-1]
                swap(arr, j , j-1);//交换两者
            }
            else
                break;
        }
    }
}

public static void swap(Object arr[], int x, int y){
    Object temp = arr[y];
    arr[y] = arr[x];
    arr[x] = temp;
}

可能有同学要问了，你那个sort(Comparable[] arr)是什么意思呢？

其实，这里是可以写成sort(int [] arr)，这样就好理解了，就是一个int类型的数组嘛。

但是，我们排序的不可能永远是一个int类型的数组，有可能我们需要排序浮点型的数组，有可能我们需要根据学生的成绩来对学生进行排名......

所以，我们就不能使用普通的比较arr[j]<arr[j-1]这种方法，来对学生的成绩进行排序，这里使用了compareTo()这种方法，我们将具体的比较方法放在了compareTo()方法中，而Comparable[] 则表示这里引用的是一个实现了Comparable接口的类，里面实现了compareTo()方法，下面是一个例子：

class Student implements Comparable<Student>{
    private String name;
    private int score;

    public Student(String name, int score){
        this.name = name;
        this.score = score;
    }

    @Override
    public int compareTo(Student o) {
        if(this.score < o.score)
            return 1;
        else if(this.score > o.score)
            return -1;
        else
            return 0;
    }

}

这样的话，我们写的排序算法就可以用来比较学生的成绩了，这里我们就不用关心comparaTo()里面具体的方法是什么，反正我们知道里面是排序的规则，而这里的规则就是学生的成绩直接的比较。

注意：这样的话，我们如果要比较一个int类型的数组，就不能直接用int类型，而要用Integer（int的包装类）类型的数组，因为只有Integer类型实现了Comparable接口，可以用compareTo()方法。

这样一来，原版的插入排序就写完了。这里我们用来写一个testSort()方法，和一个辅助类来创建一个10000条数据的随机数组，看看对这个数组进行排序需要多长的时间。

public static void testSort(Comparable[] arr){
    long startTime = System.currentTimeMillis();
    sort(arr);
    long endTime = System.currentTimeMillis();
    System.out.println("insertionSort uesTime:" + (endTime - startTime));
}

System.currentTimeMillis()用来获取当前时间，单位为ms。在运行程序的前后获取，再相减，则得到了程序运行的具体时间。

创建一个辅助类来创建随机数组：

public class sortTestHelper {
    public static Integer[] generateRandomArray(int n, int rangL, int rangR){
        assert rangR-rangL >= 0;
        Integer[] arr = new Integer[n];
        for(int i=0; i<n; i++){
            arr[i] = new Integer((int)( Math.random() * (rangR-rangL+1) )+ rangL);
        }
        return arr;
    }


    public static void printArray(Object arr[]){
        for(Object i:arr){
            System.out.print(i + " ");
        }
        System.out.println();
    }
}

generateRandomArray(int n, int L, int R) : n是数组的长度，[L , R]是数据的取值范围。我们用这个方法来创建数组。

完整的程序如下：

public class insertionSort {
    public static  void sort(Comparable[] arr){
        int n = arr.length;
        for(int i=1; i<n; i++){
            for(int j=i; j>0; j--){
                if(arr[j].compareTo(arr[j-1])<0){
                    swap(arr, j , j-1);
                }
                else
                    break;
            }
        }
    }

    public static void sort(Comparable[] arr, int l, int r){
        for(int i=l; i<=r; i++){
            Comparable e = arr[i];
            int j = i;
            for(; j>l&&e.compareTo(arr[j-1])<0; j--){
                arr[j] = arr[j-1];
            }
            arr[j] = e;
        }
    }

    public static void main(String[] args) {
        int n = 100000;
        Integer arr[] = sortTestHelper.generateRandomArray(n,1,1000);
        testSort(arr);
    }

    public static void testSort(Comparable[] arr){
        long startTime = System.currentTimeMillis();
        sort(arr);
        long endTime = System.currentTimeMillis();
        System.out.println("insertionSort uesTime:" + (endTime - startTime));
    }

    public static void swap(Object arr[], int x, int y){
        Object temp = arr[y];
        arr[y] = arr[x];
        arr[x] = temp;
    }
}

运行结果如下：

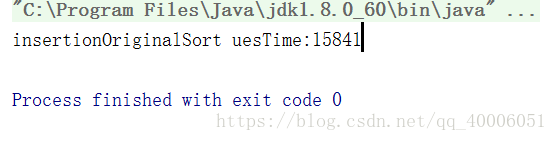
我们可以看到，仅仅是10000条数据，我们就用了15.841s。这简直是不可忍受的，我们仅仅是10000条数据，数据范围在[1,1000]，就让插入排序花了16秒的时间，简直是灾难。

自然的，我们就会生出这样一种想法，能不能让插入排序进行优化呢？让他更加快速呢？

答案是肯定的。

public static void sort(Comparable[] arr, int l, int r){
    for(int i=l; i<=r; i++){
        Comparable e = arr[i];
        int j = i;
        for(; j>l&&e.compareTo(arr[j-1])<0; j--){
            arr[j] = arr[j-1];
        }
        arr[j] = e;
    }
}

这种优化的思想就是争取让交换的次数降低，让赋值的次数降低。每次找到较小的数时，并不将他与前面的数交换，而是记录下来，将前一位的值赋值给他，一直到遇见了比他小的数或者是第一位数，则将遍历的数赋值为较小的数。

我们再看看这种优化后的算法需要的时间：

降低了一些，需要10.831秒，比原来的算法优化了30%左右。

而值得一提的是，插入算法在进行大量相同数字排序和近似有序数字排序时，其耗费的时间会大大降低，让我们来做个测试，首先在我们的辅助类中添加一个近似有序数组：

public static Integer[] generateNearlyOrderArray(int n, int swapTimes){
    Integer[] arr = new Integer[n];
    for(int i=0; i<n; i++){
        arr[i] = new Integer(i);
    }
    for(int i=0; i<swapTimes; i++){
        int posx = (int)Math.random()*n;
        int posy = (int)Math.random()*n;
        Integer temp = arr[posy];
        arr[posy] = arr[posx];
        arr[posx] = temp;
    }
    return arr;
}

进行测试：

public static void main(String[] args) {
    int n = 100000;
    Integer arr[] = sortTestHelper.generateNearlyOrderArray(n ,100);
    testSort(arr);
}

惊呆了有没有，这次只花了0.004s。这说明在近似有序数组进行排序时，插入排序的效率比起O（nlogn）的高级算法还要高效，而关于大量重复数据的排序同学们也可以自己去进行测试。

注意：原本插入排序的效率要比选择排序的效率高效，无论何种情况下都是如此，但是用java写的插入排序在一般情况下要比选择排序效率低，而用C写的话就是效率高些，如果有知道为什么的童鞋请在下方留言。