2018 Multi-University Training Contest 5——Everything Has Changed（平面几何）

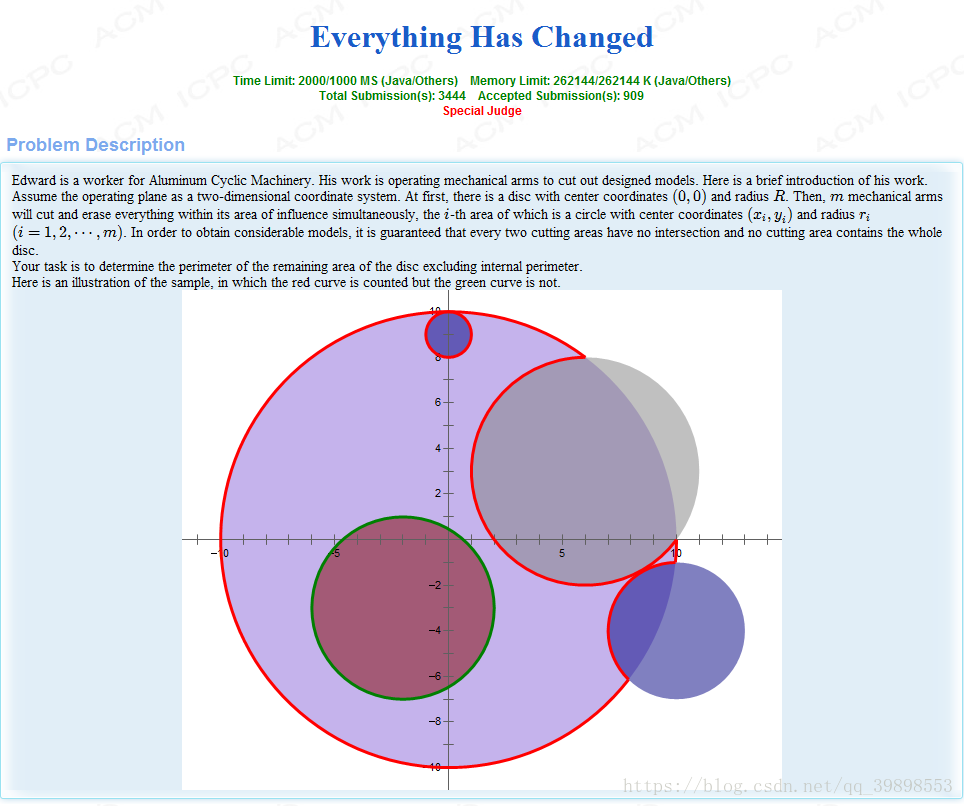
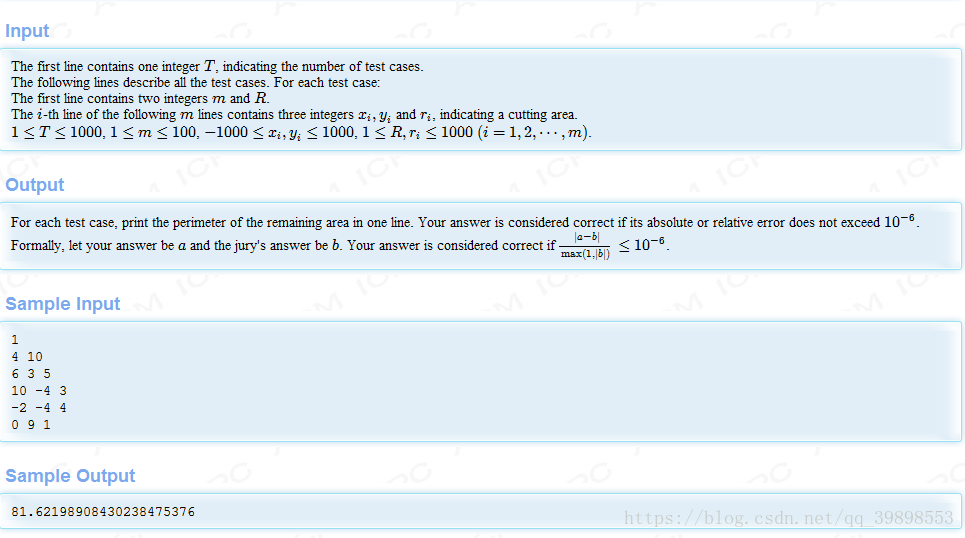
题解：

求相交圆的弧长。本题理解清楚题意后套用公式就可以了。公式推导过程如下：

1、先求出相交弦长D
假设两圆半径分别为r₁、r₂，圆心距离为d，于是r₁、r₂和d构成一个三角形，所求弦长为这个三角形d边上的高h的2倍，根据海伦公式，三角形的面积：
S＝√[p(p-r₁)(p-r₂)(p-d)]， 其中: p＝(r₁+r₂+d)/2
高h＝2S/d＝2√[p(p-r₁)(p-r₂)(p-d)] / d
弦长D＝4√[p(p-r₁)(p-r₂)(p-d)] / d
2、根据弦长求到弧长
两个圆的对应的弧长是不同的，可利用反正弦函数求得。
圆1上的弧长： C1 ＝ r₁ * arcsin { 2√[p(p-r₁)(p-r₂)(p-d)] /(dr₁) }
圆2上的弧长： C2 ＝ r₂ * arcsin { 2√[p(p-r₁)(p-r₂)(p-d)] /(dr₂) }
其中： p＝(r₁+r₂+d)/2

标程C++代码

#include <bits/stdc++.h>
using namespace std;
typedef double DB;
const DB pi = acos(-1.0);
int main() 
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        int m,R;
        scanf("%d%d", &m, &R);
        DB ans = 0, rem = pi;
        for(int i = 1; i <= m; ++i) 
        {
            int x, y, r;
            scanf("%d%d%d", &x, &y, &r);
            int dis2 = x * x + y * y;
            if(dis2 < (R - r) * (R - r) || dis2 > (R + r) * (R + r))
                continue;
            DB dis = sqrtl(dis2);//精度要求非常高时用sqrtl
            DB ang1 = acos(min(max((dis2 + R * R - r * r) / (2 * R * dis), -1.0), 1.0));
            DB ang2 = acos(min(max((dis2 - R * R + r * r) / (2 * r * dis), -1.0), 1.0));
            rem -= ang1;
            ans += 2 * r * ang2;
        }
        ans += 2 * R * rem;
        printf("%.20f\n", ans);
    }
    return 0;
}