辗转相除法(嵌套调用)
其算法过程为: 前提:设两数为a,b设其中a 做被除数,b做除数,temp为余数
1、大数放a中、小数放b中;
2、求a/b的余数;
3、若temp=0则b为最大公约数;
4、如果temp!=0则把b的值给a、temp的值给a;
5、返回第二步;
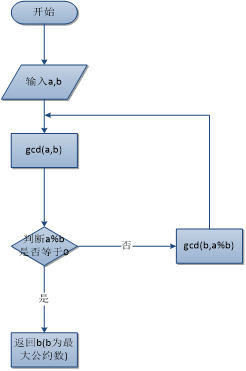
代码:
int gcd(int a, int b)
{
if (b==0)
return a;
else
return gcd(b, a % b);
}
辗转相除法(嵌套调用)
其算法过程为: 前提:设两数为a,b设其中a 做被除数,b做除数,temp为余数
1、大数放a中、小数放b中;
2、求a/b的余数;
3、若temp=0则b为最大公约数;
4、如果temp!=0则把b的值给a、temp的值给a;
5、返回第二步;

代码:
int gcd(int a, int b)
{
if (b==0)
return a;
else
return gcd(b, a % b);
}

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


