python稀疏矩阵scipy.sparse中的csr_matrix及astype('category')

1、python astype(‘category’), 编码和标签对应，categories 和 code 映射为字典

import pandas as pd
 
# 创建数据集
df = pd.DataFrame.from_dict(
            {
            'col1': ['A', 'B', 'C', 'B', 'A', 'D'],
            'col2': ['aa', 'bb', 'bb', 'aa', 'dd', 'dd'],
            'col3': ['yes', 'yes','no','no','yes','yes']
            }
            ,orient='columns')
# df 
#   col1 col2 col3
# 0    A   aa  yes
# 1    B   bb  yes
# 2    C   bb   no
# 3    B   aa   no
# 4    A   dd  yes
# 5    D   dd  yes
 
# 转换为分类数据
df = df.astype('category') # 可以指定特定的列转为分类数据 df['col1'] = df['col1'].astype('category')
 
# 将标签数据转换为编码
df_code = pd.DataFrame({col: df[col].cat.codes for col in df}, index=df.index)
 
# df_code 
#    col1  col2  col3
# 0     0     0     1
# 1     1     1     1
# 2     2     1     0
# 3     1     0     0
# 4     0     2     1
# 5     3     2     1
 
# 将编码和标签一一对应，转为字典，方便查询
df_code_dict = {col: {code: category for code, category in enumerate(df[col].cat.categories)} for col in df}
# df_code_dict 
# {'col1': {0: 'A', 1: 'B', 2: 'C', 3: 'D'},
#  'col2': {0: 'aa', 1: 'bb', 2: 'dd'},
#  'col3': {0: 'no', 1: 'yes'}}

2.1、csr_matrix索引方式1

这种方式百度介绍的较多
indptr = np.array([0, 2, 3, 6])
indices = np.array([0, 2, 2, 0, 1, 2])
data = np.array([1, 2, 3, 4, 5, 6])
csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()

输出：
array([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]])
csr中的r表示row，即为行优先。

indptr中的元素两个两个的看，前两个为0和2,表示第一行有2-0=2个元素，再在indices中选前两个元素，得到在列上的位置为0和2，填充data的元素为1和2。接在是indptr中的2和3，所以第二行有3-2=1个元素，要填充的列位置是indices 中的2，元素从data中找为3. 在接下来是indptr中的3和6，表示第三行有6-3=3个元素，要填充的位置是indices 中的0、1、2，元素从data中找为4,5,6.

2.1、csr_matrix索引方式2

根据矩阵值进行索引

df = pd.DataFrame.from_dict(
            {
            'col1': [1, 0, 2, 3, 2, 1],
            'col2': [1, 0, 1, 2, 3, 4],
            'col3': [14, 15, 10, 20, 30, 40]
            }
            ,orient='columns')
df

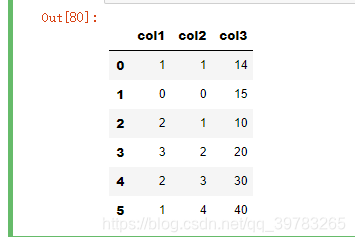
sparse_item_user = sparse.csr_matrix((df['col3'], (df['col1'], df['col2'])))
sparse_item_user.toarray()