【算法】【链表模块】二叉树空间复杂度为O(1)的遍历方法（Morris算法）

前言

当前所有算法都使用测试用例运行过，但是不保证100%的测试用例，如果存在问题务必联系批评指正~

在此感谢左大神让我对算法有了新的感悟认识！

问题介绍

原问题
遍历二叉树，空间复杂度O（1）

解决方案

1、利用二叉树的null指针进行上一个状态的保存即可
公共逻辑框架：
首先将树的现状变成

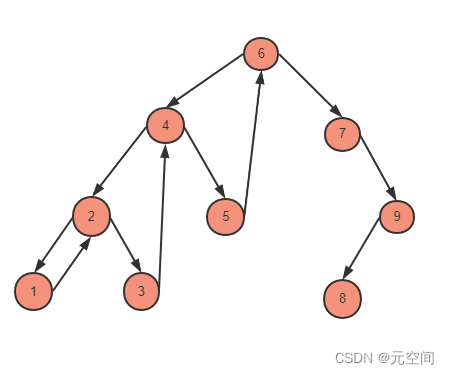
也就是每一个节点的左孩子的最右边的孩子指向该节点的父节点
先序遍历：
1、如上图，从6-4-2-1开始每一个节点都进行一次遍历链接形成上图，在遍历过程中输出每一个开头节点，也就是6421
2、当遍历到1节点时，从1节点回到2节点，并指向2的右节点3，将1节点右节点清空为null，继续遍历
中序遍历：
1、如上图，从6-4-2-1开始每一个节点都进行一次遍历链接形成上图，在遍历过程中不输出开头节点
2、当遍历到1节点时，输出1节点，从1节点回到2节点，输出2节点并到3节点，继续循环
后续遍历：
1、如上图，从6-4-2-1开始每一个节点都进行一次遍历链接形成上图，在遍历过程中不输出开头节点
2、在回到上一个节点2时，将1节点以及1节点的所有右子节点全部倒序输出，如1,32,54
3、最后将根节点以及根节点的所有右子节点输出即可

代码编写

java语言版本

public class MorrisTree {
	// 先序遍历
    public static void myMorris(MyTreeNode root){
        if (root == null){
            return;
        }
        MyTreeNode cur = root;
        while (cur != null){
            MyTreeNode left = cur.getLeft();
            if (left != null){
                while (left.getRight() != null && left.getRight() != cur){
                    left = left.getRight();
                }
                if (left.getRight() == null){
                    System.out.print(cur.getData());
                    left.setRight(cur);
                    cur = cur.getLeft();
                    continue;
                }
                // left == cur
                left.setRight(null);
                cur = cur.getRight();
            }else {
                System.out.print(cur.getData());
                cur = cur.getRight();
            }
        }
    }

	// 中序遍历
    public static void myMirrisMid(MyTreeNode root){
        if (root == null){
            return;
        }
        MyTreeNode cur = root;
        while (cur != null){
            MyTreeNode left = cur.getLeft();
            if (left != null){
                while (left.getRight() != null && left.getRight() != cur){
                    left = left.getRight();
                }
                if (left.getRight() == null){
                    left.setRight(cur);
                    cur = cur.getLeft();
                    continue;
                }
                System.out.print(cur.getData());
                left.setRight(null);
                cur = cur.getRight();
            }else {
                System.out.print(cur.getData());
                cur = cur.getRight();
            }
        }
    }
	// 后续遍历：有点麻烦
    public static void myMirrisPos(MyTreeNode root){
        if (root == null){
            return;
        }
        MyTreeNode cur = root;
        while (cur != null){
            MyTreeNode left = cur.getLeft();
            if (left != null){
                // 辅助栈，这里不通过翻转降低空间复杂度了麻烦
                Stack<MyTreeNode> stack = new Stack<>();
                stack.push(left);
                while (left.getRight() != null && left.getRight() != cur){
                    left = left.getRight();
                    stack.push(left);
                }
                if (left.getRight() == null){
                    left.setRight(cur);
                    cur = cur.getLeft();
                    continue;
                }
                // 走到这里说明left到了回到上一层的地方
                while (!stack.isEmpty()){
                    System.out.print(stack.pop().getData());
                }
                cur = left.getRight();
                left.setRight(null);
                //if (cur.getLeft() != null && cur.getLeft() != left){
                //    System.out.print(cur.getLeft().getData());
                //}
                cur = cur.getRight();
            }else {
                //System.out.print(cur.getData());
                cur = cur.getRight();
            }
        }
        cur = root;
        Stack<MyTreeNode> helper = new Stack<>();
        while (cur != null){
            helper.push(cur);
            cur = cur.getRight();
        }
        while (!helper.isEmpty()){
            System.out.print(helper.pop().getData());
        }
    }
    public static void main(String[] args) {
        MyTreeNode head = CommonUtils.getSearchMyTreeNode();
        PrintTreeDirect.myPrint(head);
        TreeUtils.printPosOrder(head);
        System.out.print("\n");
        myMirrisPos(head);
    }
 
}

c语言版本

正在学习中

c++语言版本

正在学习中

思考感悟

这道题其实很典型的利用了二叉树的无用空间来保存能够返回上一层的指针，nb的就是一个循环解决了两个问题，第一，解决了二叉树的变形，也就是右节点指向上一层。第二，解决了二叉树的恢复。可以说这个方法将二叉树的遍历转了两圈，一圈变形，一圈恢复，先中后序遍历也分别利用了两圈中的各个时机输出节点，比如先序遍历利用了变形过程中的每一个变量将父节点们都打印出来，之后将左右孩子节点分别在恢复的过程中打印出来，非常巧妙。
这道题其实需要掌握一个框架那就是“两圈框架“，首先要手写出两圈框架，变形和恢复之后，再思考应该将输出的语句填入什么时机即可。

写在最后

方案和代码仅提供学习和思考使用，切勿随意滥用！如有错误和不合理的地方，务必批评指正~
如果需要git源码可邮件给2260755767@qq.com
再次感谢左大神对我算法的指点迷津！