LeetCode#面试题 01.07.旋转矩阵自己的一点解题思路分享

本文链接：https://blog.youkuaiyun.com/qq_39668155/article/details/105365672

本文介绍了一种90°顺时针旋转矩阵的算法思路，通过分区块轮换的方式，实现了矩阵的高效旋转。代码示例清晰，详细解释了变量设置和逻辑流程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

对应LeetCode题目面试题 01.07.旋转矩阵
看了一圈大家提出的题解方案，思路都非常的有意思。我的这种思路类似于风车式的代换，但是可能理解起来会比较好一些，编码难度也可能会低上一些。

正文

首先我们要先理解这次问题的核心点，也就是90°顺时针旋转到底是什么含义？
我们通过一张图先来简单理解一下思路：
！渣图警告⚠，能力有限还望原谅
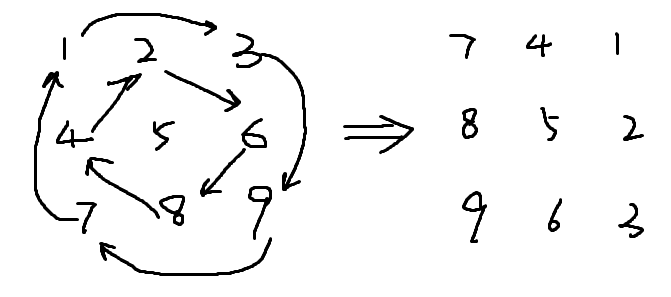
可以看到的的是其实轮换的过程是分区块的。以这个矩阵为例，就能看出来1、3、7、9是一组，2、4、6、8又是一组，这也是很多题解的初识思路是相同的。那么我们先总结一下这种轮转的通式，没有通式我们也不可能简化对吧。
$假设轮换起始点坐标为(i,j),矩阵的长度（姑且称其为长度）为length\\ 下一个轮转点的坐标为(j,length - i - 1)$
好的有了这一点前置条件后，我们再来看一张图：
这张图是一个4阶矩阵的实例，我们可以看到按照上述的分离方案，会有4组不同的轮转组存在对吧。然后我们将轮转本身归纳为一种操作，具体来说就是我们拿到一个点就能保证，这个轮转组中的数都能正确轮转了。
这一点很关键，这样我们就能看到如图中右边框中的点，只要对这些点进行轮转操作之后，就能保证整个矩阵正确转换了吧。

先说到这里，概念的东西就只有这么多了，我们先上代码，之后的细节我在后面补充：

public void rotate(int[][] matrix) {
    if(matrix == null || matrix.length < 2){
        return; 
    }
    int tempValue = 0, length = matrix.length, depth = (length + 1) >> 1, newRow = 0, newCol = 0;

    for(int i = 0; i < depth; i++){
        for(int j = i; j < length - 1 - i; j++){
            int preValue = matrix[i][j], tempRow = 0;
            newRow = j;
            newCol = length - i - 1;
            while(newRow != i || newCol != j){
                tempValue = matrix[newRow][newCol];
                matrix[newRow][newCol] = preValue;
                preValue = tempValue;
                tempRow = newRow;
                newRow = newCol;
                newCol = length - tempRow - 1;
            }
            matrix[i][j] = preValue;
        }
    }
}

给出具体的代码后，相信不少人已经明白了我的用意，之后我就大致细化一下逻辑和一些变量的设置的理由。
首先depth = （length + 1） >> 1，当然右移1其实就是除以2啦。这个变量主要是用来限制行遍历的，这个是我归纳出来的，灵感就是第二张图的右边部分的方框区域，还没有具体的证明方法，如果大家证明思路可以在评论中提出！
然后j < length - i - 1，这一点和上面一样，也是通过归纳出来的，主要是用来限制列遍历的。
内部的一个循环while(newRow != i || newCol != j)这段循环也就是为了满足轮转操作的，preValue表示前一个坐标的值，tempValue是用来临时存储这一坐标的值，newRow是下一坐标的行Index,newCol是下一坐标的列Index。
需要注意的是当前(i,j)始终是指的是最开始的坐标位置，所以matrix[i][j] = preValue是为了将这个点的值变为轮转后的值。