参考:https://blog.youkuaiyun.com/zuzhiang/article/details/78134247
单调栈,顾名思义,是栈内元素保持一定单调性(单调递增或单调递减或是其他性质)的栈。
我们假如有这样一个问题(poj3250):给定一组数,针对每个数,寻找它和它右边第一个比它大的数之间有多少个数。
如果用朴素的解法就会是双层for循环遍历,时间复杂度达到O(n^2),利用单调栈思想的解法则会降至限行时间O(n)
给一个序列10,3,7,4,12,我们将他们看作是一站好队的人,将问题看作每个人看看自己右边比自己高的人离自己有多远
最开始,10先站到一边(进栈),等待比他高的人被发现(被遍历到),接下来轮到3,他显然不比站到一边的人(10)高,那就也和10一起站(进
栈),来等比他高的人被发现.接下来到了7,这时候栈顶(3)大喊:教官,我找到右边比我高的人了,3完成了任务,高高兴兴出栈走了
(也就是说,在遍历过程中,比栈顶元素小的可以直接进栈,作为新的栈顶,它一定比栈里其它元素更早的发现比它大的右边元素).
栈里就剩下了10,10和7一比较,发现7还没自己高,没办法,还得继续等,7也顺势站到一边(进栈),等待比自己高的人...循环往复
ac代码
#include<iostream>
#include<stdio.h>
#include<stack>
#include<string.h>
const int inf = 0x3f3f3f3f;
typedef long long ll;
using namespace std;
//单调栈设置
//位置进栈,输入输出
//最后放置一个哨兵
//记录位置数组
int main()
{
int a[80010];
ll ans = 0;
int n;scanf("%d",&n);
stack<int> st;
for(int i=0; i<n; i++)
{
scanf("%d",&a[i]);
}
a[n] = inf;
//放空栈
//位置进栈
for(int bj=0; bj<=n; bj++)
{
if( st.empty() || a[bj] < a[st.top()] ) //如果栈为空或者栈顶元素比新到元素小
{
st.push(bj);//直接进栈
}
else
{
while( !st.empty() && a[bj] >= a[st.top()])
{//出栈出到栈顶元素比目标元素大。
ans = ans + bj - st.top() - 1;
st.pop();
}
st.push(bj);
}
}
printf("%lld",ans);
return 0;
}
描述
给定一个n个整数的序列以及一个非负整数d,请你输出这个序列中有多少个连续子序列(长度大于1),满足该子序列的最大值最小值之差不大于d。
连续子序列:序列1 2 3中长度大于1的连续子序列有:
-
1 2 -
2 3 -
1 2 3
输入
第一行包含两个整数n,d。
接下来一行包含n个整数。
输出
输出一个整数,表示满足条件的连续子序列个数。
样例1输入
-
8 5 -
5 5 4 8 -10 10 0 1
样例1输出
7
样例1解释
满足条件的连续子序列有:
-
5 5 -
5 5 4 -
5 5 4 8 -
5 4 -
5 4 8 -
4 8 -
0 1
这道题被提示用单调栈的时候,我是一脸懵逼的,想维护一个单调递增或者单调递减的单调栈,仔细思考思考发现都很难行通.
这是一开头对单调栈的解释: 单调栈,顾名思义,是栈内元素保持一定单调性(单调递增或单调递减或是其他性质)的栈。
那么这道题,非单调递增也不是单调递减,于是它便一定是满足其它性质的栈.
这个性质就是栈里的元素可以满足题目的条件:满足该子序列的最大值最小值之差不大于d。
用做例子,我们有下面的一个序列a,求满足最大值最小值的差不超过5的子序列个数
5 5 4 8 -7 -10 10 0 1
算法的一开始自然是5先进栈,然后整个栈的最大值最小值自然先都更新成为5,然后开始遍历整个序列,轮到第二个5,它的数值
在整个栈的最大值和最小值相差都不大于5,因此他可以进栈,同样的,4和8也都统统进入,整个栈的最小值为4,最大值为8,每一个
将要进栈的元素,都可以和栈里的元素组成连续的满足条件的子序列.
具体来说,每一个元素如果能满足条件进栈,满足条件的子序列
总数会再加上栈中的元素个数.(比如8进栈的时候,栈中已经有5 5 4, 于是满足条件的子序列总数就会+3 (4 8) (5 4 8) (5 5 4 8) )
到了-7,他不满足和栈中最大值最小值相差不大于5这个条件,于是栈清空,停! 不能急着清空,我们需要多一个判断,我们考察这样一种情况
栈中元素(20 15),当前元素为10,这时,20是要丢掉的,但是15是要保留的.
也就是说,从栈顶向下,和当前元素差不大于5的还是可以保留的,直到碰到第一个破坏了这种性质的元素停止,保留的方法是引入了一个辅助栈(具体看代码吧)
经过判断,-7的确会让栈中元素都清空,清空结束后,-7进入栈中. 接下来是-10进栈,10清空了栈进栈....循环往复
代码(笔记本连不上网了,只能这样了.代码也懒得精简了,嘿嘿嘿):

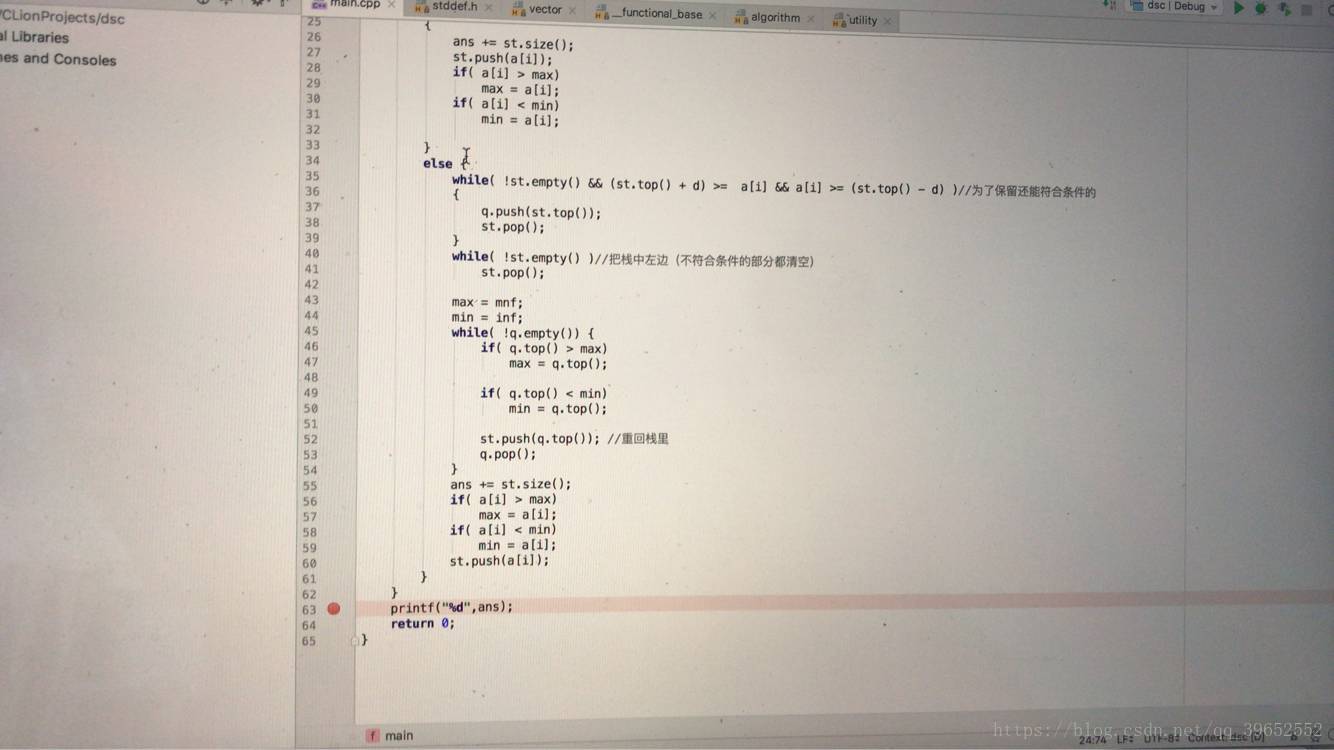
最后废话一句,类似这种序列组合的题目,都可以想想能不能用单调栈做










 本文深入讲解单调栈算法,探讨其在解决特定问题如寻找最近更大数、子序列计数等应用,通过实例演示如何利用单调栈优化算法效率。
本文深入讲解单调栈算法,探讨其在解决特定问题如寻找最近更大数、子序列计数等应用,通过实例演示如何利用单调栈优化算法效率。
















 339
339

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








