第七讲--训练神经网络下--课时16--更好的优化

归一化的作用：

当分割超平面改变时，预测分数变化较小。这样，神经网络容易训练。

-------------------------------

当各个超参数的作用不一样大（神经网络就是这样），random search 理论上更有优势。

------------------------------

sgd的问题：

（1）由于各个参数量级不一致，迭代呈之字形，很慢

（2）在接近局部极值的地方，梯度很慢，可能卡住（实际由于参数空间维度高，不会，但是慢）

（3）sgd一次一个样本，不能反映整体训练集，具有噪声。

-----------------------------------------------------------------------------------------

momentum:

(1)积累动量，在极值点附件梯度不会太小，可以冲过极值点

(2)无关方向的梯度被平均抵消了，有关方向的梯度变大了。

------------------------------------------------------------------------------------------------

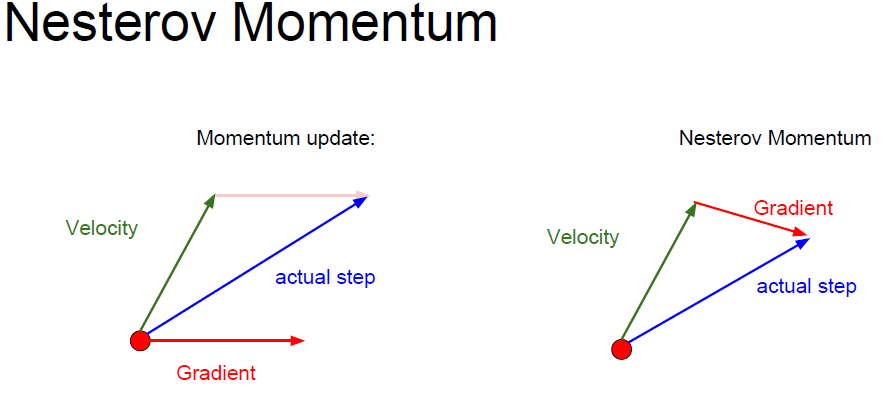
Nesterov momentum  

已知velocity，估计gradient,求和

与momentum顺序相反

-------------------------------------------------------------------------------------------

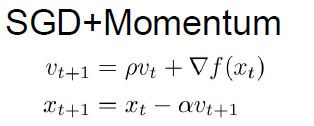
RMS是在AdaGrad基础上得到的

AdaGrad的梯度会越来越小，如果是凸优化问题，那么这样ok。但如果不是凸优化，很容易掉进局部极值里面去。

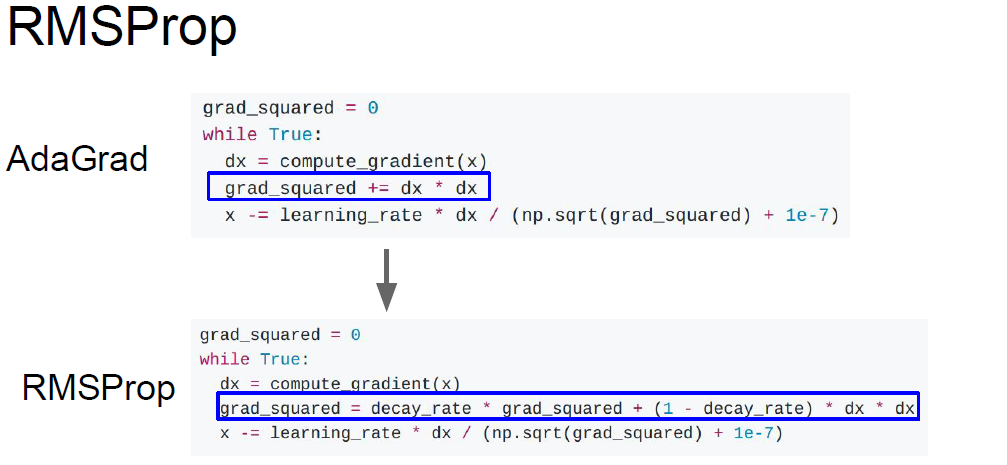
/(1-beta**t) 是为了避免最初几次迭代时，moment太小了，从而使得更新的梯度太大了，不符合实际

---------------------------------------------------------------------------------------------------

momentum 更新时容易绕路，它的更新方向大致限定在某一方向

RMS则较平滑

Adam结合了momentum和RMS，几乎是默认选择。

----------------------------------------------------------------------------------------------------

牛顿法二阶逼近（甚至不需要学习速率）海森矩阵求逆计算量大，o(N3)

拟牛顿法BFGS,LBFGS         对于mini batch效果不好，对于非凸优化问题不好（神经网络的损失函数就是非凸的） 对噪声敏感，鲁棒性差

深度学习不经常使用二阶逼近，毕竟参数太多了。

如果计算资源足够，可以试试full batch的LBGGS，一定要注意剔除noise

----------------------------------------------------------------------------------------------------------

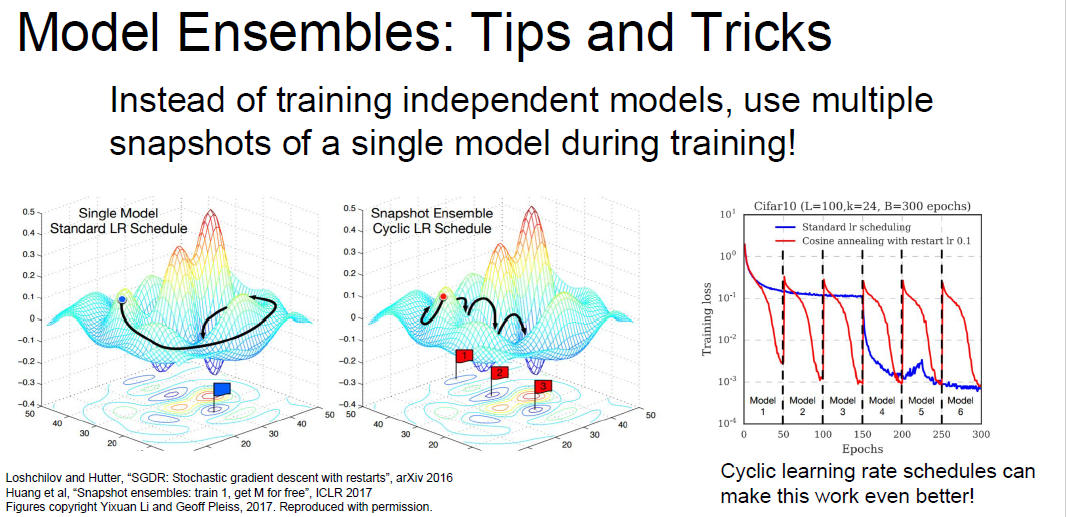
model ensembles

使用不同的初始值，不同的超参数，训练出多个网络，集成起来，一般会提高几个百分点的正确率。在数据竞赛中经常使用，但是不适合工业。

还可以记录一个模型在训练过程中不同时刻的参数，将这些集成起来。

--------------------------------------------------------------------------------------------

polyak averaging

对于一个网络训练过程中不同时期的参数做平均，然后使用平均参数作为test时候的参数。这个平均参数是集成的结果。