《动手学深度学习》第三十二天---动量法

最新推荐文章于 2025-02-11 16:34:30 发布

原创最新推荐文章于 2025-02-11 16:34:30 发布 · 397 阅读

0 ·

CC 4.0 BY-SA版权

《动手学深度学习》专栏收录该内容

37 篇文章

订阅专栏

探讨了梯度下降算法中学习率过大会导致的不收敛问题，介绍了动量法如何通过引入动量超参数来解决这一问题，使自变量能以较大步长向最优解移动，同时保持稳定性。

在梯度下降中可能存在的问题是，学习率过大，会导致不收敛。回顾一下我们使用近似的前提是：找到一个常数η（学习率）＞0，使得|??′(?)|足够小，然后通过
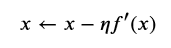
在这里插入图片描述
来迭代x，从让f(x)不断下降。但是当我们使用过大的学习率时，|??′(?)|可能会过大从而使一阶泰勒展开不再成立，这个时候无法保证迭代?会降低?(?)的值，那么x就有可能越过最优解而逐渐发散。
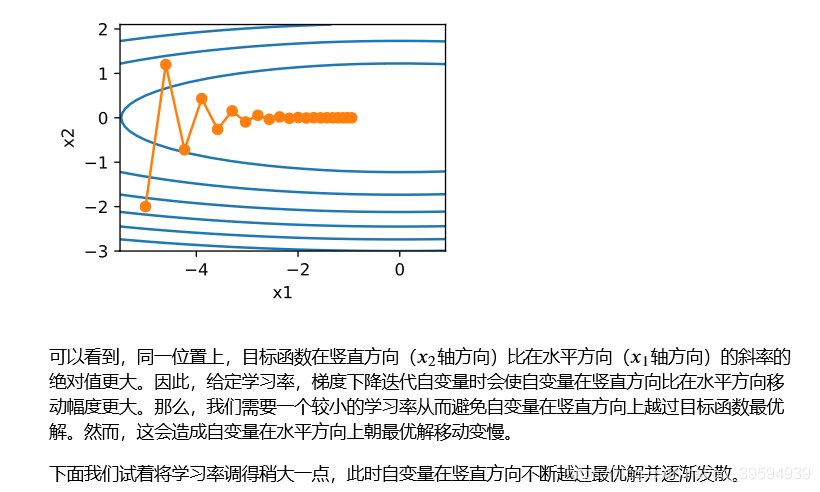
在一个二维向量的目标函数中，就可能出现在相同的学习率下，一个方向比另一个方向移动幅度更大，从而在一个方向越过最优解。
在这里插入图片描述

动量法

动量法对每次迭代的步骤做如下修改：
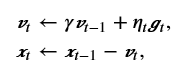
在这里插入图片描述
其中，动量超参数γ满足0<γ<1。当γ=0时，动量法等价于小批量随机梯度下降。
在动量法中，自变量在各个方向上的移动幅度不仅取决当前梯度，还取决于过去的各个梯度在各个方向上是否一致。这样，我们就可以使用较大的学习率，从而使自变量向最优解更快移动。
动量法的代码实现：

def momentum_2d(x1, x2, v1, v2):
    v1 = gamma * v1 + eta * 0.2 * x1
    v2 = gamma * v2 + eta * 4 * x2
    return x1 - v1, x2 - v2, v1, v2

eta, gamma = 0.4, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

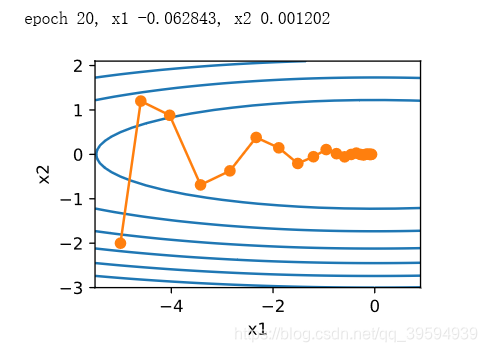
在这里插入图片描述

有梯度在水平方向上为正（向右），而在竖直方向上时正（向上）时负（向下）。这样动量法在竖直方向上的移动更加平滑，且在水平方向上更快逼近最优解。

从零开始实现

features, labels = d2l.get_data_ch7()

def init_momentum_states():
    v_w = nd.zeros((features.shape[1], 1))
    v_b = nd.zeros(1)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        v[:] = hyperparams['momentum'] * v + hyperparams['lr'] * p.grad
        p[:] -= v

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.5}, features, labels)  # 超参数中多了动量超参数

简洁实现

d2l.train_gluon_ch7('sgd', {'learning_rate': 0.004, 'momentum': 0.9},
                    features, labels)
                    # 只需要在Trainer实例中通过momentum来指定动量超参数即可使用动量法。