一.非(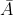 )
)
非就是相反的.
| A | |
| 1 | 0 |
| 0 | 1 |
电路图:

![]()
二.与(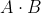 )
)
A与B就是只有A,B同时为1,结果才为1(下表粉色所示),其余为0.
| A | B | R |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
由上图中蓝色可见:
与遵守 1.交换律
另外与还遵守
2.结合律
3.互补律
4.幂等律
5.狄摩根定律
电路图:

三.或(A+B)
A或B只有A,B同时为0,结果才为0(下表粉色所示),否则为1;
| A | B | R |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
同样上图中蓝色可见
"或"也遵守 1.交换律 A+B=B+A
2. 结合律 A+(B+C)=(A+B)+C
3.互补律 A+
=1
4.幂等律 A+A=A
5.狄摩根定律
以上"或"的运算规律可与"与"的对比
除此之外,"与"和"或"还遵守如下规律:
1.吸收律 A·(A+B)=A 和
A+A·B=A
证明 A·(A+B)=A A B S 1 1 1 1 0 1 0 1 0 0 0 0 A始终等于S
证明A+A·B=A A B S 1 1 1 1 0 1 0 1 0 0 0 0 A始终等于S
2.分配律 A·(B+C)=A·B+A·C 和
A+ (B·C)=(A+B)·(A+C)
A·(B+C)=R A B C R 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1
A·B+A·C=R A B C R 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 所以 A·(B+C)=A·B+A·C
3. 重叠律
同理
电路图:

四.异或
我们先列出异或的真值表
| A | B | R |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
找其中R = 1 行(图中绿色)
把这里的A和B写成逻辑与,如果是0写成"非"
得
再把它们逻辑或连接
得R =
电路图:

![]()
其实上图中的或门可以去掉,直接将两电路并联.







 本文详细介绍了逻辑门的基本概念,包括非、与、或、异或等逻辑运算的真值表及其电路实现方式,并探讨了这些逻辑运算所遵循的重要规律如交换律、结合律、互补律等。
本文详细介绍了逻辑门的基本概念,包括非、与、或、异或等逻辑运算的真值表及其电路实现方式,并探讨了这些逻辑运算所遵循的重要规律如交换律、结合律、互补律等。
















 2830
2830

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








