哈希查找算法，结构的定义，初始化，闭散列和开散列如何增加，删除，查找数据。

哈希查找算法

最普通的查找方法就是遍历整个数据，然后找到所查找的数，它的时间复杂度一般为O(n)。而哈希查找是用一个结构体数组存储所有数据，然后对所要查找的数，求它的哈希地址（一般就是数组的下标，求下标的方式是哈希函数，将输入数据（本例是字符串）转化为整型数字），从而直接找到此数，哈希查找的时间复杂度是O(1)。

闭散列

图解，结合文字再进行理解：

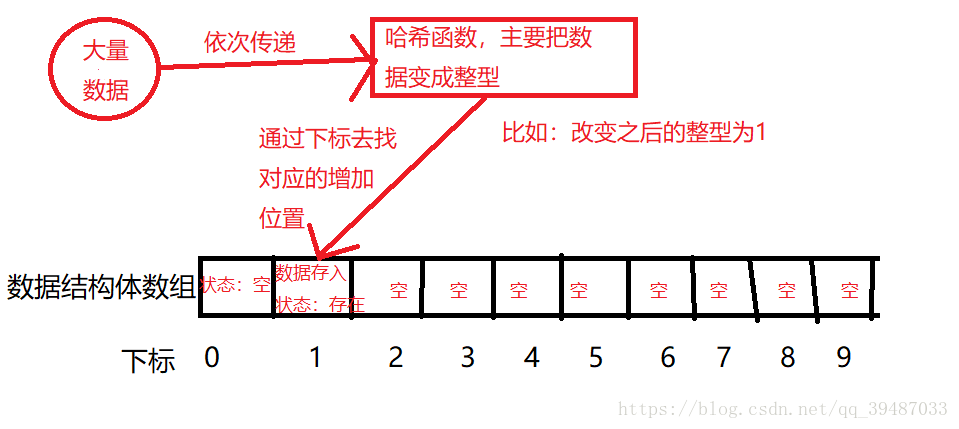
哈希结构的定义

一般哈希查找的存储结构体如下定义：

typedef int (*STINT)(const char * str);    //这是一个函数指针类型的重命名

typedef char* Type;
typedef enum {EXIST,DELETE,EMPTY}State;

typedef struct DataState
{
	Type data;
	State state;
}DataState;


typedef struct HashStruct
{
	DataState* Dasa;    //哈希数组
	int Size;              //记录已经添加的数据量
	int capacity;      //哈希数组的容量大小
	int tatol;       	//记录除了空位置剩余的位置数量
	STINT _STInt;   //创建函数指针，函数为哈希函数
}HashStruct,*pHashStruct;

哈希冲突

哈希地址的函数做不到让所有的数据都得到不同的哈希地址，所以可能会有不同的数得到相同的哈希地址，这叫做哈希冲突。
由于哈希冲突的存在，并且数组对应的下标只能保存一个数据，那么就必须让每个下标附带一个状态，来表示它是否已经储存数据。所以用一个结构体数组来保存数据。

哈希结构的初始化

哈希结构的初始化比较简单，就是给所有成员赋初值。数据值因为还没增加不用管，每个数组下标对应的状态是空，容量初值赋为10。代码如下：

void InitHashSearch(pHashStruct phs,STINT STInt)
{
	int i = 0;
	assert(phs);
	phs->capacity = 10;
	phs->Dasa = (DataState*)malloc(sizeof(DataState)*phs->capacity);
	for(i=0 ;i<phs->capacity ;i++)
		phs->Dasa[i].state = EMPTY;
	phs->Size = 0;
	phs->tatol = 0;
	phs->_STInt = STInt;    // 给哈希函数赋值，看第二个形参
}

哈希结构的增加数据

增加数据就得借助哈希函数了，将我们所输入的数据（本例是字符串）转化为整型作为下标，从而直接存入到哈希结构体的数组中去，具体看代码和注释：

int InsertHashSearch(pHashStruct phs,Type data)
{
	int ret = HashCode(phs,data);              //利用哈希函数得到哈希地址（数组下标）
	assert(phs);
	if(IsChangeC(phs))                                //判断数据量是否达到负载因子
		CheckCapacity(phs);			//如果达到了，就扩容。
	while(phs->Dasa[ret].state != EMPTY)		//判断此位置的状态是否  不是空
	{
		if(phs->Dasa[ret].data == data)		//如果不是，还要判断数据是否已经存在
			return 0;
		ret++;		//判断为不是，说明已经产生了哈希冲突，
		                //此地址之前已经有数据了，就往后找空位置，这个下面详细解释
	}
	phs->Dasa[ret].data = data;        //循环停止，说明找到空位置了 ，就在此位置增加元素
	phs->Dasa[ret].state = EXIST;    //将此位置的状态赋值为存在数据
	phs->Size++;                              //数据量+1
	phs->tatol++;
	return 1;                  
}

线性探测

就是循环里面的ret++，虽然产生了哈希冲突，但是让地址往后++，直到找到状态为空的地址，这叫做线性探测。采用线性探测，实现起来非常简单，缺陷是： 一旦发生哈希冲突，所有的冲突连在一起，容易产生数据“堆积”，即：不同关键码占据了可利用的空位置，使得寻找某关键 码的位置需要许多次比较，导致搜索效率降低。缓解的办法就是代码提到的负载因子。（除了线性探测还有二次探测）

负载因子

这里要引入一个名词是负载因子，和上面的哈希冲突有关。因为当为了减少哈希冲突的发生，我们必须控制负载因子，负载因子是除了空位置剩余的位置数量tatol和容量capacity的比值（如果比值越高那么发生哈希冲突的概率越高），一般以0.7为标准。
用tatol的原因是因为增加元素的时候只找存在状态，删除的状态虽然没有元素，但是会影响增加。

哈希结构的查找和删除数据

查找和增加的初步类似，都是先用哈希函数找数据地址，代码如下：

int FindHashSearch(pHashStruct phs,Type data)
{
	int ret = HashCode(phs,data);
	int pre = ret;
	assert(phs);
	while(phs->Dasa[ret].state != EXIST || strcmp(phs->Dasa[ret].data,data) != 0)
	{		 //这个循环只有当数据地址状态不为EXIST，并且要删除元素和地址元素相同
		ret++;
		if(ret == phs->capacity)   	  //如果走到末尾就从初始位置开始
			ret = 0;
		if(pre == ret)		  //如果走了一圈还没找到，就返回0 
			return 0;
	}
	return 1;
}

删除数据和查找数据一样，既然能找到，那自然能删除，代码如下：

int PopHashSearch(pHashStruct phs,Type data)
{
	int ret = HashCode(phs,data);
	int pre = ret;
	assert(phs);
	while(phs->Dasa[ret].state != EXIST || strcmp(phs->Dasa[ret].data,data) != 0)   
	{    		    //这个循环只有当数据地址状态不为EXIST，并且要删除元素和地址元素相同
		ret++;
		if(ret == phs->capacity)     //如果走到末尾就从初始位置开始
			ret = 0;
		if(pre == ret)                 //如果走了一圈还没找到，就返回0 
			return 0;
	}
	phs->Dasa[ret].state = DELETE;     //将状态值为删除
	phs->Size--;
	return 1;
}

需要注意的是删除之后，虽然状态从存在变成了删除，但是原来的数据还在。

哈希结构的扩容

当负载因子达到一定值时，就要进行扩容，才能保证哈希冲突的低触发率。说到这里先看一下我所使用的哈希函数：

int StrToInt(const char * str)    //  这就是将字符串转化为整型
{
	unsigned int seed = 131; // 31 131 1313 13131 131313
    unsigned int hash = 0;     
	while (*str )     
	{          
		hash = hash * seed + (*str++);     
	}      
	return (hash & 0x7FFFFFFF); 
}

int HashCode(pHashStruct cur,Type data)
{
	return cur->_STInt(data) % cur->capacity;      //求哈希地址的时候将整型取模容量
}

由此可知，哈希函数由容量决定，扩容的话容量会发生变化，所以哈希函数也会变，不仅影响之后增加的数据，而且之前已经增加的数据哈希地址也需要重新赋值，不然查找的时候就出错了。代码如下：

void CheckCapacity(pHashStruct phs)
{
	int i,place;
	pHashStruct cur = phs;
	int Capacity = cur->capacity;
	DataState* newhash = NULL;
	//1.创建新空间
	newhash = (DataState*)malloc(sizeof(DataState)*cur->capacity*2);
	if(NULL == newhash)
	{
		assert(0);
		return;
	}
	cur->capacity = cur->capacity*2;     //扩容大小为原来容量的两倍
	cur->Size = 0; 			 //下面要重新添加旧元素所以先将size置为0
	for(i=0 ;i<cur->capacity ;i++)
		newhash[i].state = EMPTY;
	//2.拷贝旧空间
	for(i=0 ;i<Capacity ;i++)
	{
		if(cur->Dasa[i].state != EXIST)
			continue;
		place = HashCode(cur,cur->Dasa[i].data);     //新空间用新的容量
		newhash[place].data = cur->Dasa[i].data;
		newhash[place].state = EXIST;
		cur->Size++;
	}
	//3.释放旧空间
	free(cur->Dasa);
	cur->Dasa = newhash;
}

扩容分为三步：
1.创建新空间
2.拷贝旧数据
3.释放旧空间

开散列

开散列和闭散列不同的是，闭散列在每个哈希地址上存的是数据，有别的相同哈希地址的数据来到时，就用探测的方法去找空位置将其添加进哈希结构。而开散列在每个哈希地址上存的是一个链表的头结点，当有新的相同哈希地址的数据到来时，只需要头插进入此地址的链表即可。

开散列哈希结构的定义和初始化函数

typedef int (*STINT)(int num);

typedef int OH_type;

typedef struct OpenList
{
	OH_type data;
	struct OpenList* next;
}OpenList,*pOpenList;


typedef struct OpenHash
{
	pOpenList* _openlist;    //一个指针数组，保存链表的头结点
	int size;
	int capacity;
	STINT _STInt; 
}OpenHash,*pOpenHash;

初始化函数注意，需要给链表的头指针数组开辟动态内存空间：

void InitOpenHash(pOpenHash oph,STINT stint)
{
	int i;
	assert(oph);
	oph->capacity = 10;
	oph->size = 0;
	oph->_STInt = stint;
	oph->_openlist = (pOpenList*)malloc(sizeof(pOpenList)*oph->capacity);
	for(i=0 ;i<oph->capacity ;i++)
		oph->_openlist[i] = NULL;
}

开散列哈希结构的增加、删除和查找数据

void InsertOpenHash(pOpenHash oph,OH_type d)
{
	pOpenList cur = NULL;
	int place = HashCode(oph,d);
	assert(oph);
	if(oph->size == oph->capacity)   //判断是否需要扩容
		CheckCapacity(oph);
	cur = oph->_openlist[place];
	while(cur)
	{
		if(d == cur->data)
			return;
		cur = cur->next;
	}
	cur = BuyOpenHash(d);
	cur->next = oph->_openlist[place];
	oph->_openlist[place] = cur;
	oph->size++;
}

开散列判断是否需要扩容没有负载因子，因为它没有探测。

int DeleteOpenHash(pOpenHash oph,OH_type d)
{
	pOpenList del = NULL;
	pOpenList pre = NULL;
	int place = HashCode(oph,d);
	assert(oph);
	del = oph->_openlist[place];
	pre = del;
	if(del->next == NULL)    
	{
		if(del->data != d)
			return 0;
		oph->_openlist[place] = NULL;
		free(del);
		del = NULL;
		oph->size--;
		return 1;
	}
	while(del->next != NULL)
	{
		if(del->data == d)
		{
			pre->next = del->next;
			free(del);
			del = NULL;
			oph->size--;
			return 1;
		}
		pre = del;
		del = del->next;
	}
	return 0;
}

删除的时候注意判断一下是否需要改变链表的头指针。

pOpenList FindOpenHash(pOpenHash oph,OH_type d)
{
	pOpenList cur = NULL;
	int place = HashCode(oph,d);
	assert(oph);
	cur = oph->_openlist[place];
	while(cur)
	{
		if(cur->data == d)
			return cur;
		cur = cur->next;
	}
	return NULL;
}

开散列哈希结构的扩容

类似闭散列，需要注意的是重新赋值可以和释放旧空间同时进行。

void CheckCapacity(pOpenHash oph)
{
	pOpenList* newlist = NULL;
	int i,place;
	pOpenList cur = NULL;
	pOpenList del = NULL;
	int newcapacity = oph->capacity;
	oph->capacity = oph->capacity*2;
	newlist = (pOpenList*)malloc(sizeof(pOpenList)*oph->capacity);
	if(NULL == newlist)
	{
		assert(0);
		return;
	}
	for(i=0 ;i<oph->capacity ;i++)
		newlist[i] = NULL;
	for(i=0 ;i<newcapacity ;i++)
	{
		cur = oph->_openlist[i];
		while(cur)
		{
			del = cur;
			place = HashCode(oph,cur->data);
			BuyOpenHash(cur->data)->next = newlist[place];
			newlist[place] = BuyOpenHash(cur->data);
			cur = cur->next;
			free(del);
			del = NULL;
		}
	}
	oph->_openlist = newlist;
}