LeetCode HOT 100 —— 48.旋转图像

题目

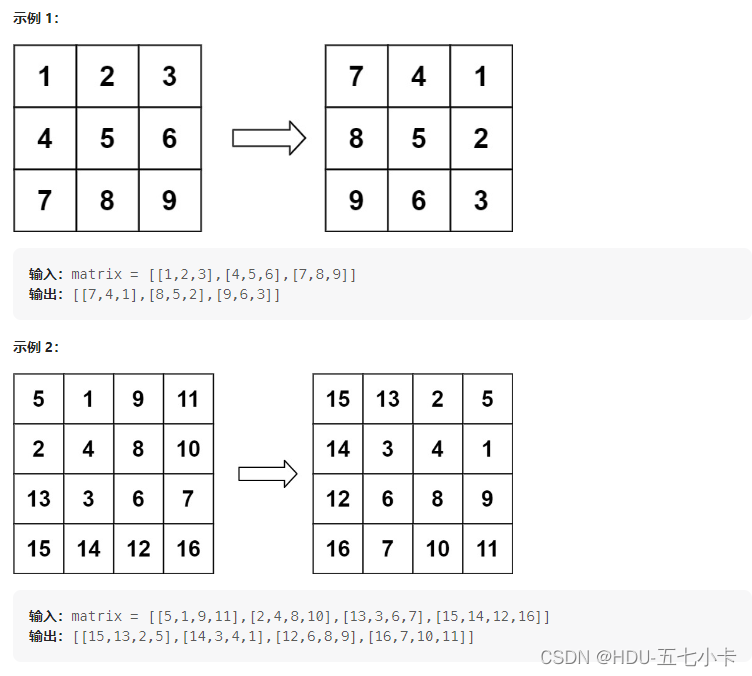
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

思路

方法一：使用辅助数组

可以得出规律，将图像旋转90度后，原来矩阵的第一行，相应的出现在了倒数第一列的位置，并且第一行的x元素在旋转后正好是倒数一列的第x个元素，第 i 行也是类似…

可以得出规律：

对于矩阵中第 i 行的第 j 个元素，在旋转后，它出现在倒数第 i 列的第 j 个位置。

用代码表示就是（注意矩阵的行列从0开始计算）：
matrix[row][col]在旋转之后的新位置为matrix[col][n - row - 1]

然后用一个和matrix大小相同的辅助数组，临时存储旋转后的数组，遍历原矩阵matrix的每一个元素存到辅助数组中，然后把结果复制到原矩阵中即可

java代码如下：

class Solution {
	public void rotate(int[][] matrix){
		int n = matrix.length;
		int[][] matrix_new = new int[n][n]; 
		for(int i = 0; i < n ; i++){
			for(int j = 0; j < n; j++){
				matrix_new[j][n - i - 1] = matrix[i][j];
			}
		}
		for(int i = 0; i < n; i++){
			for(int j = 0; j < n; j++){
				matrix[i][j] = matrix_new[i][j];
			}
		}
	}
}

时间复杂度：O（n^2）
空间复杂度：O（n^2），严格来说不算原地旋转，因为不是O（1）的空间复杂度

方法二：原地旋转

其实可以在方法一的基础上进行优化

注意到，matrix[col][n - row - 1] = matrix[row][col]，这里不能进行原地旋转的原因是，如果直接将原数组的值matrix[row][col]赋给原数组的matrix[col][n - row - 1]的位置，那么原数组的matrix[col][n - row - 1]值就会被覆盖掉，所以这里可以采用一个临时变量temp来暂存matrix[col][n - row - 1]的值，可以保证即使被覆盖了，仍然能找回matrix[col][n - row - 1]的值
即：

temp = matrix[col][n - row - 1];
matrix[col][n - row - 1] = matrix[row][col];

这里需要继续去判断matrix[col][n - row - 1]旋转后到了哪个位置，以此类推：
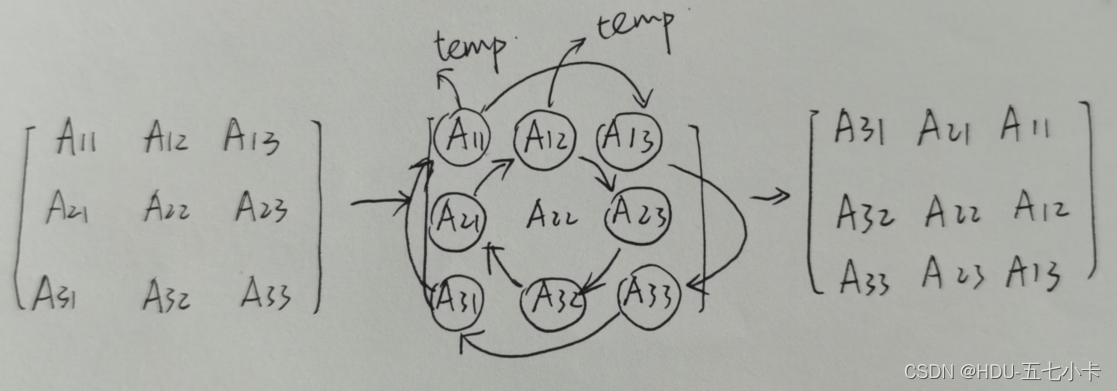
这四项处于一个循环之中，每一项旋转后的位置就是下一项所在的位置，即用一个临时变量完成这四项的原地交换即可

matrix[row][col]
matrix[col][n−row−1]
matrix[n−row−1][n−col−1]
matrix[n−col−1][row]

知道了如何原地旋转矩阵之外，还需要枚举哪些位置（即循环多少次）

• 对于n为偶数时，需要枚举n^2/4=(n/2)×(n/2)个位置
• 对于n为奇数时，由于中心的位置经过旋转后位置不变，需要枚举 （n^2-1）/4 = (n-1)/2 * （n+1）/2个位置
  两者选最大的，分别为n/2和（n+1）/2
  替换过程如下图所示（以奇数边为例）：
  
  java代码如下：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < (n + 1) / 2; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
}

时间复杂度：O（n^2）
空间复杂度：O（1），原地旋转

方法三：用翻转代替旋转

先通过上下翻转，再主对角线翻转（注意哈，主对角线是↘，副对角线是↗）

推导过程：

• 对于上下翻转，只需要将矩阵上面元素和矩阵下面元素进行交换，即matrix[row][col] —>水平轴翻转—>matrix[n−row−1][col]
• 对于主对角线翻转，只需要枚举对角线左下侧的元素，和右上侧的元素进行交换，即matrix[row][col] —>主对角线翻转—>matrix[col][row]

联立二式可得：matrix[row][col]—>水平轴翻转—>matrix[n−row−1][col]—>主对角线翻转—>matrix[col][n - row - 1]

和方法一、二中的等式一样：matrix[col][n−row−1]=matrix[row][col]

java代码如下：

class Solution{
	public void rotate(int[][] matrix){
		int n = matrix.length;
		//上下翻转
		for(int i = 0; i < n / 2; i++){//行只需要遍历到一半即可
			for(int j = 0; j < n; j++){
				int temp = matrix[i][j];
				matrix[i][j] = matrix[n - i - 1][j];
				matrix[n - i - 1][j] = temp;
			}
		}
		//主对角线↘翻转
		for(int i = 0; i < n; i++){
			for(int j = 0; j < i; j++){
				int temp = matrix[i][j];
				matrix[i][j] = matrix[j][i];
				matrix[j][i] = temp;
			}
		}
	}
}