三着色问题

最新推荐文章于 2024-06-03 23:07:11 发布

大知无涯者

最新推荐文章于 2024-06-03 23:07:11 发布

阅读量2.6k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：数据结构与算法

本文链接：https://blog.youkuaiyun.com/qq_39464369/article/details/88555491

数据结构与算法专栏收录该内容

25 篇文章

订阅专栏

本文深入探讨了图着色算法的实现，通过具体的代码示例，详细解释了如何使用递归和回溯策略来解决图的着色问题。文章展示了算法的流程，包括如何检查颜色分配的有效性以及如何在图中递归地应用颜色。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

算法代码

#include "stdafx.h"
#include<stdio.h>
#include<stdlib.h>
const int N=5;
int c[N+1]={0,};
int map[N+1][N+1]={
	{0,0,0,0,0,0},
	{0,0,1,1,0,0},
	{0,1,0,0,1,1},
	{0,1,0,0,1,1},
	{0,0,1,1,0,1},	
	{0,0,1,1,1,0}
};

void display()
{
	printf("         %d         \n",c[1]);
	printf("       *    *     \n");
    printf("     *        *   \n");
	printf("   *            *     \n");
	printf("  %d              %d\n",c[2],c[3]);
	printf("  * *          * *     \n");    
	printf("  *   *      *   *   \n");	
	printf("  *     *  *     *     \n");
	printf("  *     *  *     *   \n");
	printf("  *  *        *  *    \n");
	printf("  %d * * * *  *   %d \n",c[4],c[5]);
	printf("                 \n");
	printf("\n");	
}
bool iscolor(int c[],int k)	
{
	for(int i=1,sum=0;i<=N&&i!=k;i++)
		if(map[k][i]&&c[i]==c[k])
			return false;
		return true;
}
int GraphColorRec(int k)
{
	for(int color=1;color<=3;color++) 
	{
	 	c[k]=color;
	  	if(iscolor(c,k))		//部分解或解
		{
	     	if(k<N) 					//部分解
		     	GraphColorRec(k+1); 	//进入下一个结点
	     	else			 				//是解
		      	display();
		}
	}
	c[k]=0;
	return 0;
}
int GraphColor()
{
	int k=1;		//k表示当前处理的结点号
	while (k>0)	 	//k=0表示无法后退，程序终止。
	{
		while (c[k]<3)	       		//最多三种着色
		{
			c[k]=c[k]+1;			//下一种颜色
			if (iscolor(c,k))	//部分解或解
			{
				if (k==N) 		//完全解
					display();
		        else	 		//部分解
					k++;		//前进（下一个结点）
			}
		}
		c[k--]=0 ;			//清0后回溯
	}
	return 0;
}
int main()
{
	//GraphColorRec(1);
	GraphColor();
	printf("\n");
	return 0;
}

测试结果

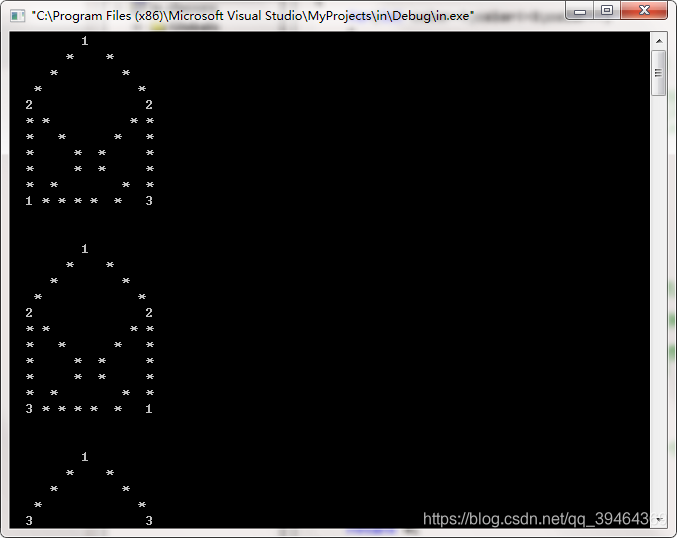
在这里插入图片描述