Coursera-AndrewNg线性回归编程作业
准备工作
从网站上将编程作业要求下载解压后,在Octave中使用cd命令将搜索目录移动到编程作业所在目录中,博主的所有数据文件都在桌面,路径移动如下图所示:
单变量线性回归
STEP1 PLOTTING THE DATA
在处理数据之前,可以通过离散的点来描绘它,在一个2D的平面里,把ex1data1中的内容读取到X变量和y变量中,用m表示数据长度。代码如下:
data = load('ex1data1.txt');
X = data(:,1);
y = data(:,2);
m = length(y);
接下来通过图像描绘出来。
plotData(X,y);
ylabel('Profit in $10,000s');
xlabel('Population of City in 10,000s');
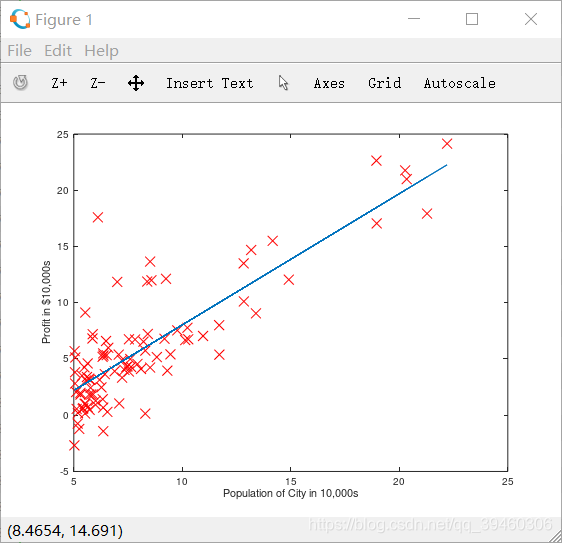
得到的图像如图所示,就是原始的数据的直观表示。
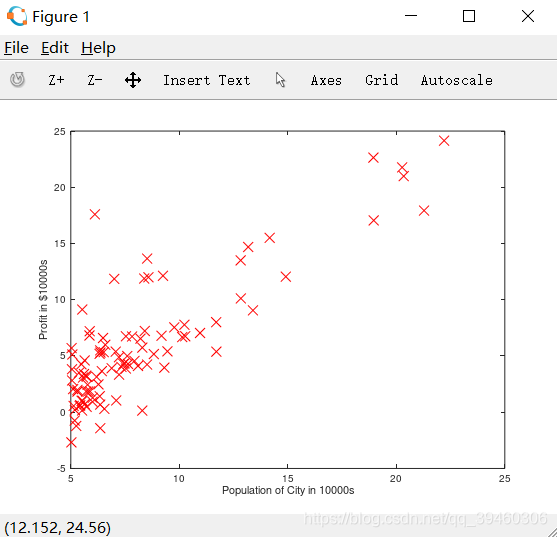
STEP2 GRADIENT DESCENT
然后通过梯度下降对参数θ进行线性回归。
依照课程所得出的步骤方法
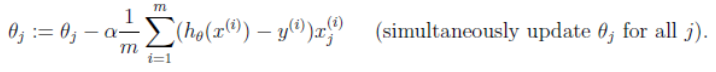
迭代更新
计算θ值函数computeCost.m:
function J = computeCost(X,y,theta)
%COMPUTECOST compute cost for linear regression
%J=COMPUTECOST(X,y,theta) computes the cost of using theta as the parameter for linear regression to fit the data points in X and y
%Initialize some useful values
m = length(y); %number of training examples
%return the following variables correctly
J=0;
%Compute the cost of a particular choice of theta
%set J to the cost
%===========YOUR CODE HERE============
prediction = X*theta;
sqr=(prediction-y).^2;
J=1/(2*m)*sum(sqr)
%=======================================
end
梯度下降函数gradientDescent.m:
function[theta,J_history]=gradientDescent(X,y,theta,alpha,num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
%======================YOU CODE HERE========================
% Instructions: Perform a single gradient step on the parameter vector theta
prediction = X * theta;
error = prediction - y;
sums = X' * error;
delta = 1 / m * sums;
theta = theta - alpha * delta;
%============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
绘图函数plotData(x,y):
function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure
% PLOTDATA(x,y) plots the data points and gives the figure axes labels of population and profit.
%====================YOU CODE HERE=========================
plot(x,y,'rx','MarkerSize',10);
ylabel('Profit in $10,000s');
xlabel('Population of City in 10,000s');
%============================================================
end
根据以上函数,进行线性回归:
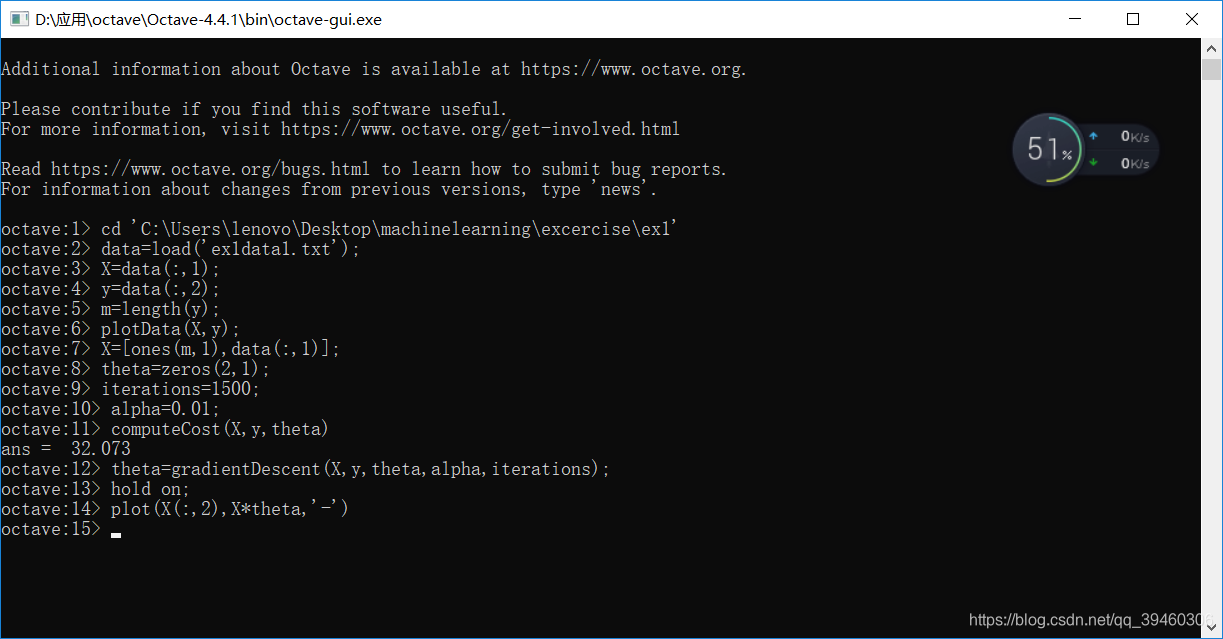
代码文本如下:
octave:1> cd 'C:\Users\lenovo\Desktop\machinelearning\excercise\ex1'
octave:2> data=load('ex1data1.txt');
octave:3> X=data(:,1);
octave:4> y=data(:,2);
octave:5> m=length(y);
octave:6> plotData(X,y);
octave:7> X=[ones(m,1),data(:,1)];
octave:8> theta=zeros(2,1);
octave:9> iterations=1500;
octave:10> alpha=0.01;
octave:11> computeCost(X,y,theta)
ans = 32.073
octave:12> theta=gradientDescent(X,y,theta,alpha,iterations);
octave:13> hold on;
octave:14> plot(X(:,2),X*theta,'-')
结果如如图所示:
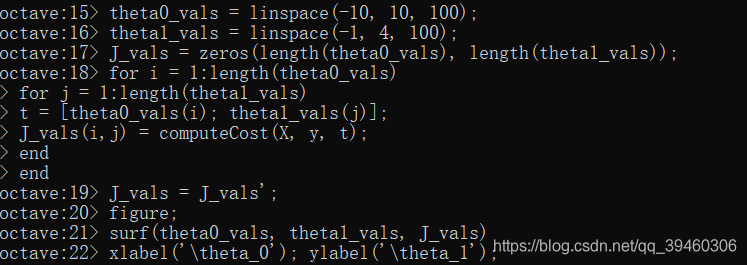
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
结果如图所示:
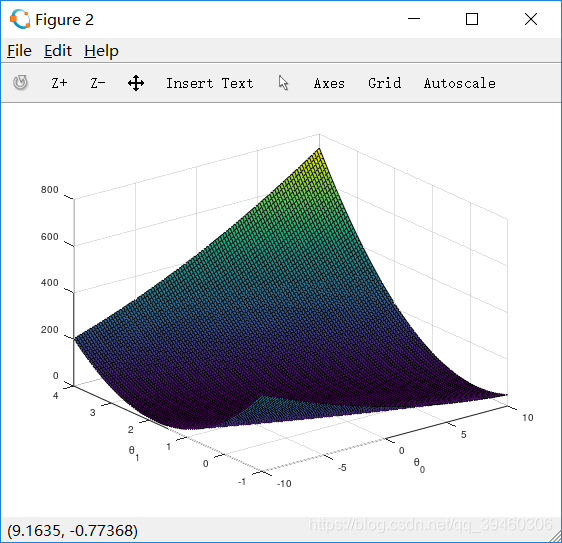
根据数据绘制等高线图:

代码文本如下:
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
结果图如图所示:
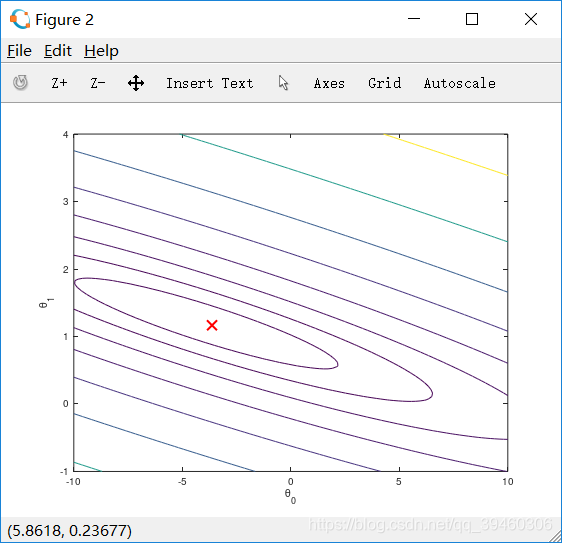





 本文详细介绍了在Coursera上Andrew Ng教授的机器学习课程中,如何使用Octave进行单变量线性回归的编程作业。从数据加载、绘图、梯度下降算法实现到成本函数计算,再到最终的线性回归结果展示,全面覆盖了线性回归的学习和实践过程。
本文详细介绍了在Coursera上Andrew Ng教授的机器学习课程中,如何使用Octave进行单变量线性回归的编程作业。从数据加载、绘图、梯度下降算法实现到成本函数计算,再到最终的线性回归结果展示,全面覆盖了线性回归的学习和实践过程。
















 2686
2686

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








