二叉树

最新推荐文章于 2021-11-15 18:59:59 发布

Robotheadhead

最新推荐文章于 2021-11-15 18:59:59 发布

阅读量139

点赞数 1

CC 4.0 BY-SA版权

分类专栏：刷题

本文链接：https://blog.youkuaiyun.com/qq_39422316/article/details/89764885

刷题专栏收录该内容

9 篇文章

订阅专栏

博客围绕特殊二叉树展开，已知二叉树由正整数组成且最后一个结点是n，要计算结点m所在子树的结点数。给出输入输出描述及示例，思路是找规律，计算结点m所在层数和最大层数，再计算各层子树节点数，还给出递归参考代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

链接：https://www.nowcoder.com/questionTerminal/f74c7506538b44399f2849eba2f050b5
题目
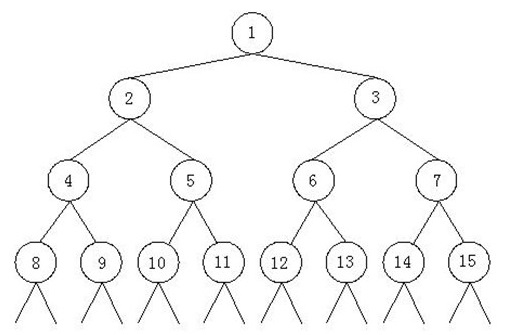
在这里插入图片描述
如上所示，由正整数1，2，3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是，结点m所在的子树中一共包括多少个结点。比如，n = 12，m = 3那么上图中的结点13，14，15以及后面的结点都是不存在的，结点m所在子树中包括的结点有3，6，7，12，因此结点m的所在子树中共有4个结点。

输入描述:
输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。

输出描述:
对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。

示例1
输入
3 12
输出
4

思路
非常笨地找规律…

计算结点m所在层数level和最大层数maxlevel
计算第i层（i从level到maxlevel-1），子树中的节点数，ans += pow(2,i-level)
计算maxlevel层，子树中节点数
如果n < ll（第maxlevel层，子树最左边的节点），ans保持不变
否则，ans += min(n-ll+1,rr-ll+1) = min(n-ll+1, pow(2,maxlevel-level) )
其中，ll = m * pow(2,maxlevel-level)，rr = ll + pow(2,maxlevel-level) - 1

代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>

using namespace std;
int main(){
    int m,n;
    while(cin>>m>>n){
        int maxlevel = log(n)/log(2) + 1;
        int level = log(m)/log(2) + 1;
        if(level<maxlevel){
            int ans = 0; 

            for(int i=level;i<maxlevel;i++){
                ans += pow(2,i-level);
            }
            //cout << "ans here = " << ans <<endl;
            int ll = m * pow(2,maxlevel-level);
            int tmp = pow(2,maxlevel-level);
            

            int rr = ll + tmp -1;
            //cout<<"ll="<<ll <<" ,rr="<<rr<<endl;
            if(n >= ll){
                ans += min(n-ll+1,tmp);
            }
            cout << ans << endl;
        }
        else cout << 1 << endl;
    }
}

参考代码：递归
节点数 = 左子树的节点数 + 右子树的节点数 + 1（自身）

链接：https://www.nowcoder.com/questionTerminal/f74c7506538b44399f2849eba2f050b5
来源：牛客网 @|讨厌鬼|

#include<stdio.h>
int countNode(int m,int n){
    if(m>n) return 0;
    return countNode(2*m,n)+countNode(2*m+1,n)+1;
} 
int main(){
    int m,n;
    while(scanf("%d%d",&m,&n)!=EOF){
        if(m==0&&n==0) break;
        printf("%d\n",countNode(m,n));
    }
    return 0;
}